Two vessels have the same base area but differnent shapes. The first vessel takes twice the vloume of water that the second vessel requires to fill up to a paricular common height . Is the force exerted by water on the base of the vessel the same in the two case? If so, why do the vessels filled with water to that same height give different reading on a weighting scale ?
(i) As the two vessels have liquid to same height and the vessels have same base area, the force exerted = pressure × base area will be same as pressure
=hpg.
(ii) Since the volume of water in vessel 1 is greater than in vessel (2) the weight of water = volume × density × h, so weight of first vessel will be greater than the water in second vessel.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PROPERTIES OF MATTEREXERCISE - Long Answer Type Questions (5 Marks)
1 Videos
- PROPERTIES OF MATTERBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PROPERTIES OF MATTEREXERCISE - NUMERICALS
23 Videos
- PROPERTIES OF MATTERBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PROPERTIES OF MATTEREXERCISE - Short Answer Type Questions (2 Marks)
25 Videos
- NEWTON'S LAWS OF MOTIONBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Laws Of Motion
20 Videos
- ROTATIONAL MOTION BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ROTATIONAL MOTION EXERCISE - MULTIPLE CHOICE QUESTIONS
20 Videos
Similar Questions
Two vessels have the same base area but differnent shapes. The first vessel takes twice the vloume of water that the second vessel requires to fill up to a paricular common height . Is the force exerted by water on the base of the vessel the same in the two case? If so, why do the vessels filled with water to that same height give different reading on a weighting scale ?
View SolutionTwo identical cylindrical vessels have the same base area but are filled with different volumes of water . The forces on the bases of the two vessels are same .
View Solution
Knowledge Check
The height of water in a vessel is h. The vessel wall of width b is at an angle θ to the vertical. The net force exerted by the water on the wall is
 A13ρbh2gcosθB12bh2ρgC12ρbh2gsecθDZero
A13ρbh2gcosθB12bh2ρgC12ρbh2gsecθDZeroTwo vessels A and B of different shapes have the same base area and are filled with water up to the same height h (see figure). The force exerted by water on the base is FA for vessel A and FB for vessel B. The respective weights of the water filled in vessels are WA and WB. Then
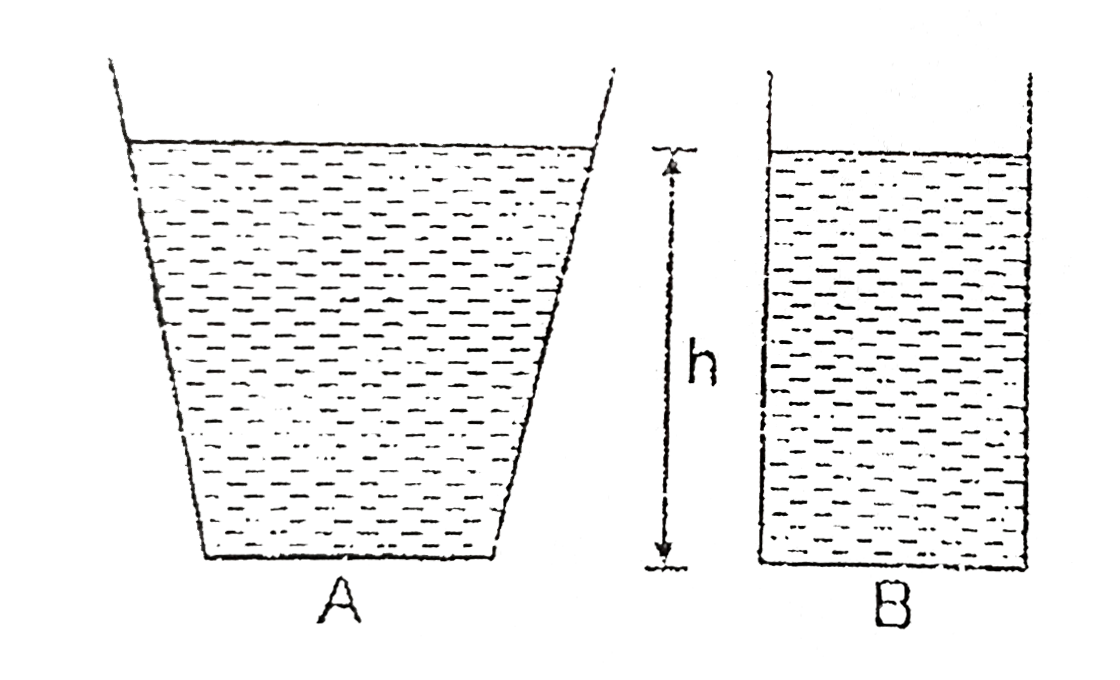 AFA>FB,WA>WBBFA=FB,WA>WBCFA=FB,WA<WBDFA>FB,WA=WB
AFA>FB,WA>WBBFA=FB,WA>WBCFA=FB,WA<WBDFA>FB,WA=WBTwo vessels A and B of different shapes have the same base area and are filled with water up to the same height h (see figure). The force exerted by water on the base is FA for vessel A and FB for vessel B. The respective weights of the water filled in vessels are WA and WB. Then
 AFA>FB,WA>WBBFA=FB,WA>WBCFA≡FB,WA<WBDFA>FB,WA=WB
AFA>FB,WA>WBBFA=FB,WA>WBCFA≡FB,WA<WBDFA>FB,WA=WB
A vessel consists of two plane mirrors at angles (as shown in figure). The vessel is filled with water. The total deviation in incident ray is
View SolutionA vessel consists of two plane mirrors at right angles (as shown in figure). The vessel is filled with water. The total deviation in incident ray is
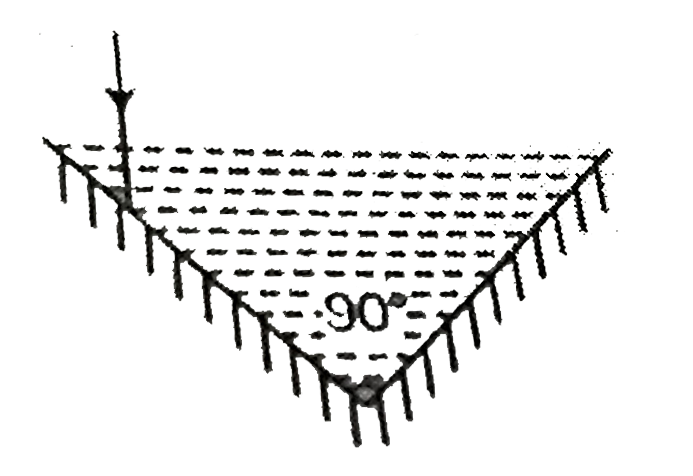
View SolutionA vessel consists of two plane mirrors at right angles as shown in figure. The vessel is filled with water. The toal deviation in incident ray is

View SolutionTwo vessels of the same volume contain the same gas at same temperature. If the pressure in the vessels is in the ratio of 1 : 2, then
View SolutionA vessel in the form of a truncated cone has base area a1 and top area a2. It is filled to the brim with a liquid. The force at the bottom of the vessel is
View Solution
