A ray of light is incident on the surface of a glass plate of thickness . I fthe angle of incidence is small, the emerging ray would be displaced side ways by an amount
n = refractive index of glass)
The correct Answer is:B
In ,
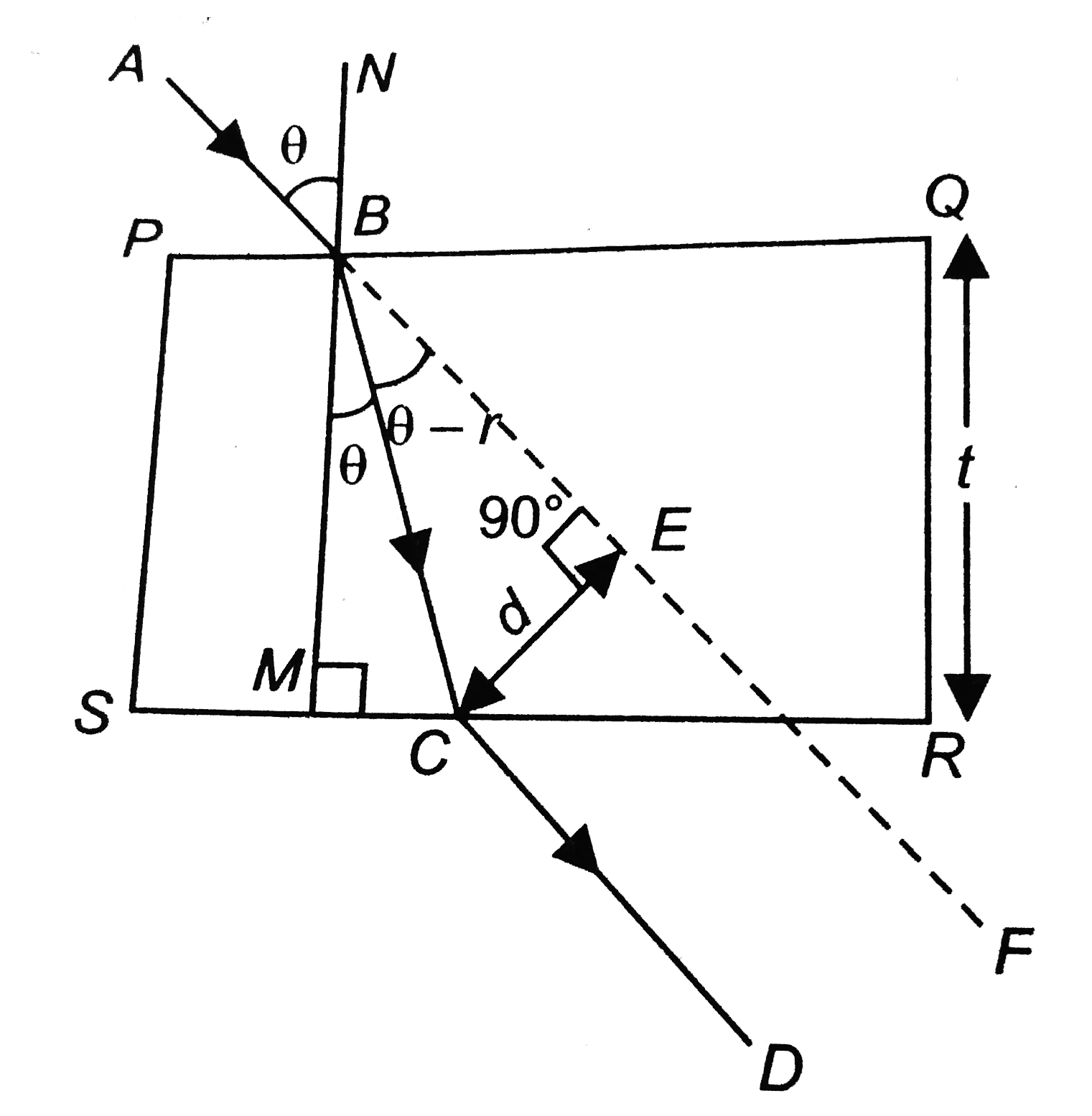
or
IN ,
or
From Eqs. (i) and (ii), we get
or
or
If is the refractive index of material of slab (glass)
w.r.t air, then
For small angle,
or and
and if is small]
or
Topper's Solved these Questions
- MOCK TESTBOOK - A2ZCHAPTER - MOCK TESTEXERCISE - Mock Test 3
44 Videos
- MOCK TESTBOOK - A2ZCHAPTER - MOCK TESTEXERCISE - Mock Test 3
44 Videos
- MAGNETISM AND MATTERBOOK - A2ZCHAPTER - MAGNETISM AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
- NUCLEAR PHYSICSBOOK - A2ZCHAPTER - NUCLEAR PHYSICSEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
A ray of light is incident on the surface of a glass plate of index of refraction 1.55 at the polarizing angle. Calculate the angle of refraction.
View SolutionA ray of light is incident on the surface of a glass plate of refractive index 1.6 at polarzing angle. Calculate the angles of reflection and refraction.
View Solution
Knowledge Check
A ray of light is incident on the surface of a glass plate of thickness t. If the angle of incidence θ is small, the emerging ray would be displaced side ways by an amount
(Take n = refractive index of glass)Atθn/(n+1)Btθ(n−1)/nCtθn/(n−1)Dtθ(n+1)/nA ray of light is incident on a parallel slab of thickness t and refractive index n. If the angle of incidence θ is small, than the lateral displacement in the incident and emergent ray will be
Atθ(n−1)nBtθnCtθnn−1Dtθ(n+1)nA ray of light is incident on the surface of plate of glass of refractive index 1.5 at the polarising angle. The angle of refraction of the ray will be
A33.7∘B23.7∘C43.7∘D53.7∘
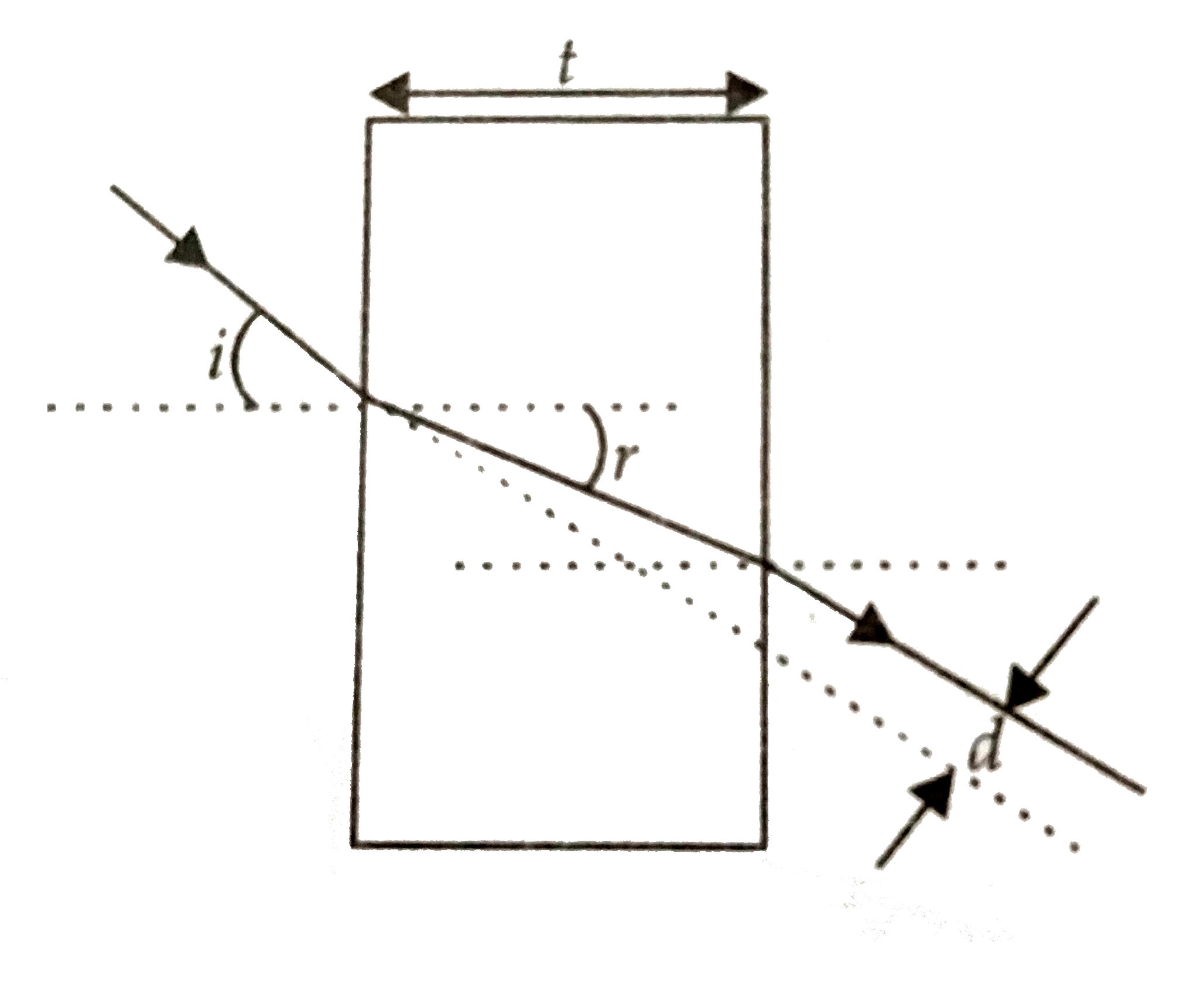
A rays of light is incident on a thick slab of glass of thickness t as shown in figure. The emergent ray is parallel to the incident ray but displaced sideways by a distance d. If the angles are small then d is
View SolutionA ray of unpolarised light is incident on a glass plate at the polarising angle of 57∘ .
Now,
View SolutionA ray of light is incident on a glass slab of thickness t, at an angle i,r is the angle of refraction in the glass slab. Distance travelled in the glass slab is
View SolutionA ray of unpolarised light is incident on a glass plate at the polarising angle θp. Then
View SolutionA ray of light is incident on the surface of a glass plate at an angle of incidence equal to Brewster's angle ϕ. If μ represents the refractive index of glass with respect to air, then the angle between reflected and refracted rays is
View Solution
