There are N cells in the circuit of figure. The emf and internal resistance of each cell is E and r respectively. The points A and B in the circuit divide the circuit into n and (N−n)cells. The current in the circuit is
E/r
nE/r
NE/nr
zero
The correct Answer is:A
To find the current in the circuit with N cells, each having an emf of E and an internal resistance of r, we can follow these steps:
Step 1: Understand the Configuration
We have N cells in the circuit, and they are divided into two parts by points A and B. One part contains n cells, and the other part contains N−n cells.
Step 2: Calculate the Total EMF
The total emf contributed by the n cells is:
\(
\text{EMF from } n \text{ cells} = n \cdot E
\)
The total emf contributed by the N−n cells is:
\(
\text{EMF from } (N - n) \text{ cells} = (N - n) \cdot E
\)
Thus, the net emf in the circuit is:
\(
\text{Net EMF} = n \cdot E + (N - n) \cdot E = N \cdot E
\)
Step 3: Calculate the Total Internal Resistance
The internal resistance contributed by the n cells is:
\(
\text{Resistance from } n \text{ cells} = n \cdot r
\)
The internal resistance contributed by the N−n cells is:
\(
\text{Resistance from } (N - n) \text{ cells} = (N - n) \cdot r
\)
Thus, the total internal resistance in the circuit is:
\(
\text{Total Resistance} = n \cdot r + (N - n) \cdot r = N \cdot r
\)
Step 4: Apply Ohm's Law to Find Current
Using Ohm's law, the current I in the circuit can be calculated as:
\(
I = \frac{\text{Net EMF}}{\text{Total Resistance}} = \frac{N \cdot E}{N \cdot r}
\)
This simplifies to:
\(
I = \frac{E}{r}
\)
Final Answer
The current in the circuit is:
\(
I = \frac{E}{r}
\)
---
We have N cells in the circuit, and they are divided into two parts by points A and B. One part contains n cells, and the other part contains N−n cells.
The total emf contributed by the n cells is:
\(
\text{EMF from } n \text{ cells} = n \cdot E
\)
The total emf contributed by the N−n cells is:
\(
\text{EMF from } (N - n) \text{ cells} = (N - n) \cdot E
\)
Thus, the net emf in the circuit is:
\(
\text{Net EMF} = n \cdot E + (N - n) \cdot E = N \cdot E
\)
The internal resistance contributed by the n cells is:
\(
\text{Resistance from } n \text{ cells} = n \cdot r
\)
The internal resistance contributed by the N−n cells is:
\(
\text{Resistance from } (N - n) \text{ cells} = (N - n) \cdot r
\)
Thus, the total internal resistance in the circuit is:
\(
\text{Total Resistance} = n \cdot r + (N - n) \cdot r = N \cdot r
\)
Using Ohm's law, the current I in the circuit can be calculated as:
\(
I = \frac{\text{Net EMF}}{\text{Total Resistance}} = \frac{N \cdot E}{N \cdot r}
\)
This simplifies to:
\(
I = \frac{E}{r}
\)
The current in the circuit is:
\(
I = \frac{E}{r}
\)
Topper's Solved these Questions
- MOCK TESTBook:A2ZChapter:MOCK TESTExercise:Mock Test 3
Explore 44 Videos
- MOCK TESTBook:A2ZChapter:MOCK TESTExercise:Mock Test 3
Explore 44 Videos
- MAGNETISM AND MATTERBook:A2ZChapter:MAGNETISM AND MATTERExercise:Section D - Chapter End Test
Explore 30 Videos
- NUCLEAR PHYSICSBook:A2ZChapter:NUCLEAR PHYSICSExercise:Section D - Chapter End Test
Explore 29 Videos
Similar Questions
In the circuit shown if the internal resistance of each cell is r, then the rate at which the chemical energy of ε1 is being consumed is
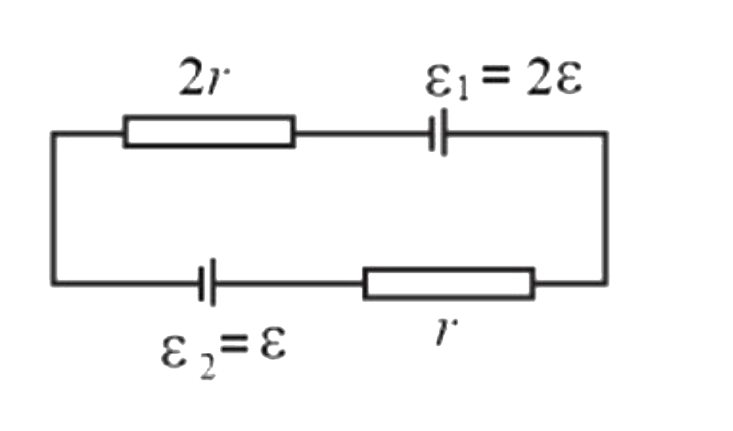
View Solutionn-identical cells each of emf E and internal resistance r are connected in series. Find the expression for current in the circuit given below

View Solution
Knowledge Check
In the circuit shown in fig. the cell has emf 10V and internal resistance 1Ω
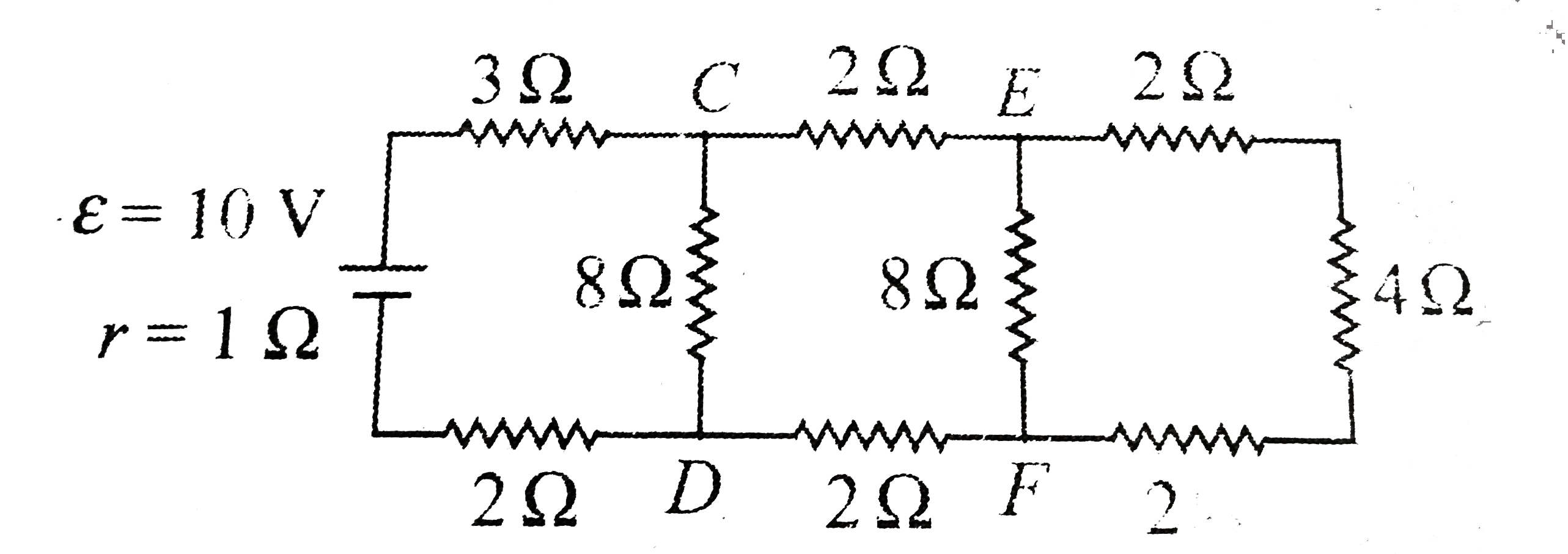 AThe current through the 3Ω resistor is 1A.BThe currents through the 3Ω resistor is 0.5 A.CThe currents through the 4Ω resistor is 0.5 ADThe current through the 4Ω resistor is 0.25 A.
AThe current through the 3Ω resistor is 1A.BThe currents through the 3Ω resistor is 0.5 A.CThe currents through the 4Ω resistor is 0.5 ADThe current through the 4Ω resistor is 0.25 A.In a closed circuit, the e.m.f. and internal resistance of the generator are E and r respectively. If the external resistance in the circuit is R, then Ohm's law has the form
AI=ERrBI=ERCI=ErDI=E(R+r)N identical current sources each of emf E and internal resistance r are connected to form a closed loop as shown in figure. The potential difference between points A and B which divides the circuit into n and (N-n) units is
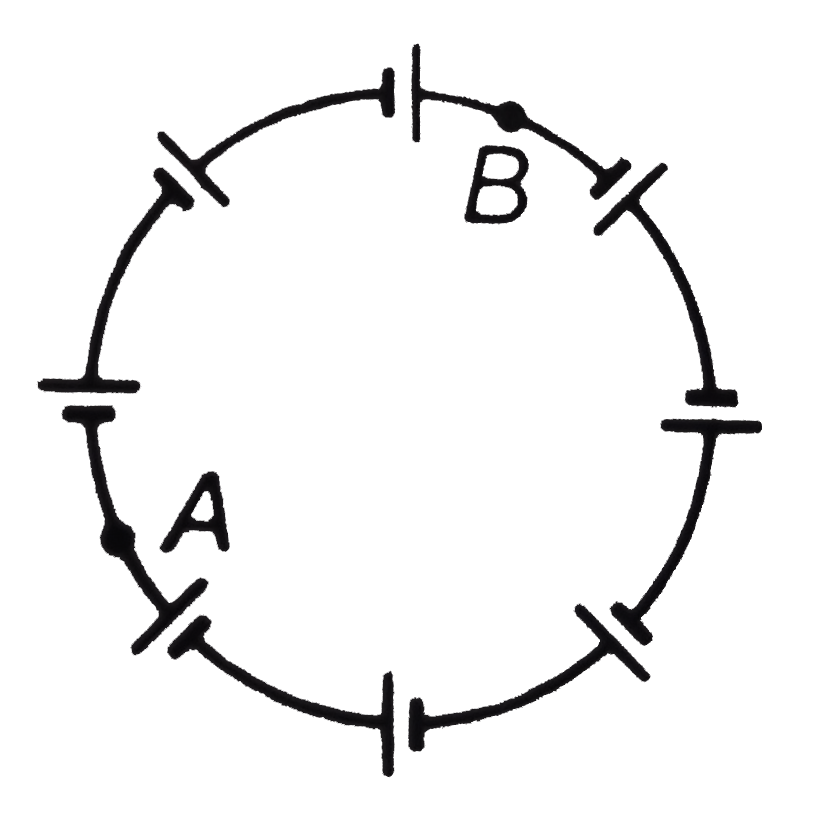 ANEB(N−n)ECnEDzero
ANEB(N−n)ECnEDzero

In the circuit shown in figure. Determine the current in the resistance CD and equivalent resistance between the points A and B. the iternal resistance of the cell is negligible.
View SolutionA cell has terminal voltage 2V in open circuit and internal resistance of the given cell is 2Ω If 4A of current is flowing between points P and Q in the circuit and then the potential difference between P and Q is
View SolutionAn external resistance R is connected to a cell of internal resistance r. The current in the circuit is maximum when
View SolutionFour cells, each of emf E and internal resistance r, are connected in series across an external resistance reverse. Then, the current in the external circuit is
View SolutionThere are n cells, each of emf E and internal resistance r, connected in series with an external resistance R. One of the cells is wrongly connected, so that it sends current in the opposite direction. The current flowing in the circuit is
View Solution

