The point charges Q and −2Q are placed at some distance apart. If the electirc field at the location of Q is E, the electric field at the location of −2Q will be
−3E2
−E
−E2
−2E
The correct Answer is:C
To solve the problem, we need to determine the electric field at the location of the charge −2Q due to the charge Q. We will follow these steps:
Step 1: Understand the setup
We have two point charges:
- Charge Q at point A
- Charge −2Q at point B
The distance between the two charges is D.
Step 2: Calculate the electric field at the location of charge Q
The electric field E at the location of charge Q due to the charge −2Q can be expressed using Coulomb's law:
\(
E = \frac{1}{4 \pi \epsilon_0} \cdot \frac{-2Q}{D^2}
\)
This electric field E is directed towards the charge −2Q since it is negative.
Step 3: Calculate the electric field at the location of charge −2Q
Now, we need to find the electric field at the location of charge −2Q due to charge Q. The electric field E' at the location of charge −2Q can be expressed as:
\(
E' = \frac{1}{4 \pi \epsilon_0} \cdot \frac{Q}{D^2}
\)
This electric field E' is directed away from the charge Q since it is positive.
Step 4: Relate the two electric fields
From the previous steps, we have:
- Electric field at Q: \( E = \frac{-2Q}{4 \pi \epsilon_0 D^2} \)
- Electric field at −2Q: \( E' = \frac{Q}{4 \pi \epsilon_0 D^2} \)
Step 5: Find the relationship between E and E'
To find the relationship between E and E', we can express E' in terms of E:
\(
E' = -\frac{1}{2} E
\)
This means that the electric field at the location of −2Q is half the magnitude of the electric field at Q, but in the opposite direction.
Final Answer
Thus, the electric field at the location of −2Q is:
\(
E' = -\frac{E}{2}
\)
We have two point charges:
- Charge Q at point A
- Charge −2Q at point B
The electric field E at the location of charge Q due to the charge −2Q can be expressed using Coulomb's law:
\(
E = \frac{1}{4 \pi \epsilon_0} \cdot \frac{-2Q}{D^2}
\)
This electric field E is directed towards the charge −2Q since it is negative.
Now, we need to find the electric field at the location of charge −2Q due to charge Q. The electric field E' at the location of charge −2Q can be expressed as:
\(
E' = \frac{1}{4 \pi \epsilon_0} \cdot \frac{Q}{D^2}
\)
This electric field E' is directed away from the charge Q since it is positive.
From the previous steps, we have:
- Electric field at Q: \( E = \frac{-2Q}{4 \pi \epsilon_0 D^2} \)
- Electric field at −2Q: \( E' = \frac{Q}{4 \pi \epsilon_0 D^2} \)
To find the relationship between E and E', we can express E' in terms of E:
\(
E' = -\frac{1}{2} E
\)
This means that the electric field at the location of −2Q is half the magnitude of the electric field at Q, but in the opposite direction.
Thus, the electric field at the location of −2Q is:
\(
E' = -\frac{E}{2}
\)
Topper's Solved these Questions
- MOCK TESTBook:A2ZChapter:MOCK TESTExercise:Mock Test 3
Explore 44 Videos
- MOCK TESTBook:A2ZChapter:MOCK TESTExercise:Mock Test 3
Explore 44 Videos
- MAGNETISM AND MATTERBook:A2ZChapter:MAGNETISM AND MATTERExercise:Section D - Chapter End Test
Explore 30 Videos
- NUCLEAR PHYSICSBook:A2ZChapter:NUCLEAR PHYSICSExercise:Section D - Chapter End Test
Explore 29 Videos
Similar Questions
Charges Q and -2Q are placed at some distance. The locus of points in the plane of the charges where the potential is zero will be :
View SolutionTwo point charges+ q and-q are placed at distanced apart. What are the points at which the resultant field is parallel to the line joining the two charges ?
View Solution
Knowledge Check
Two point charges Q and −3Q are placed at some distance apart. If the electric field at the location of Q is E then at the locality of −3Q, it is
A−EBE/3C−3ED−E/3Two points charges q and -2q are placed some distance d apart. If the electric field at the location of q is E, that at the location of -2q is
A−E2B−2ECE2D−4ETwo charges 4q and q are placed 30 cm. apart. At what point the value of electric field will be zero
A10 cm. away from q and between the chargeB20 cm. away from q and between the chargeC10 cm. away from q and out side the line joining the charge.D10 cm. away from 4q and out side the line joining them.
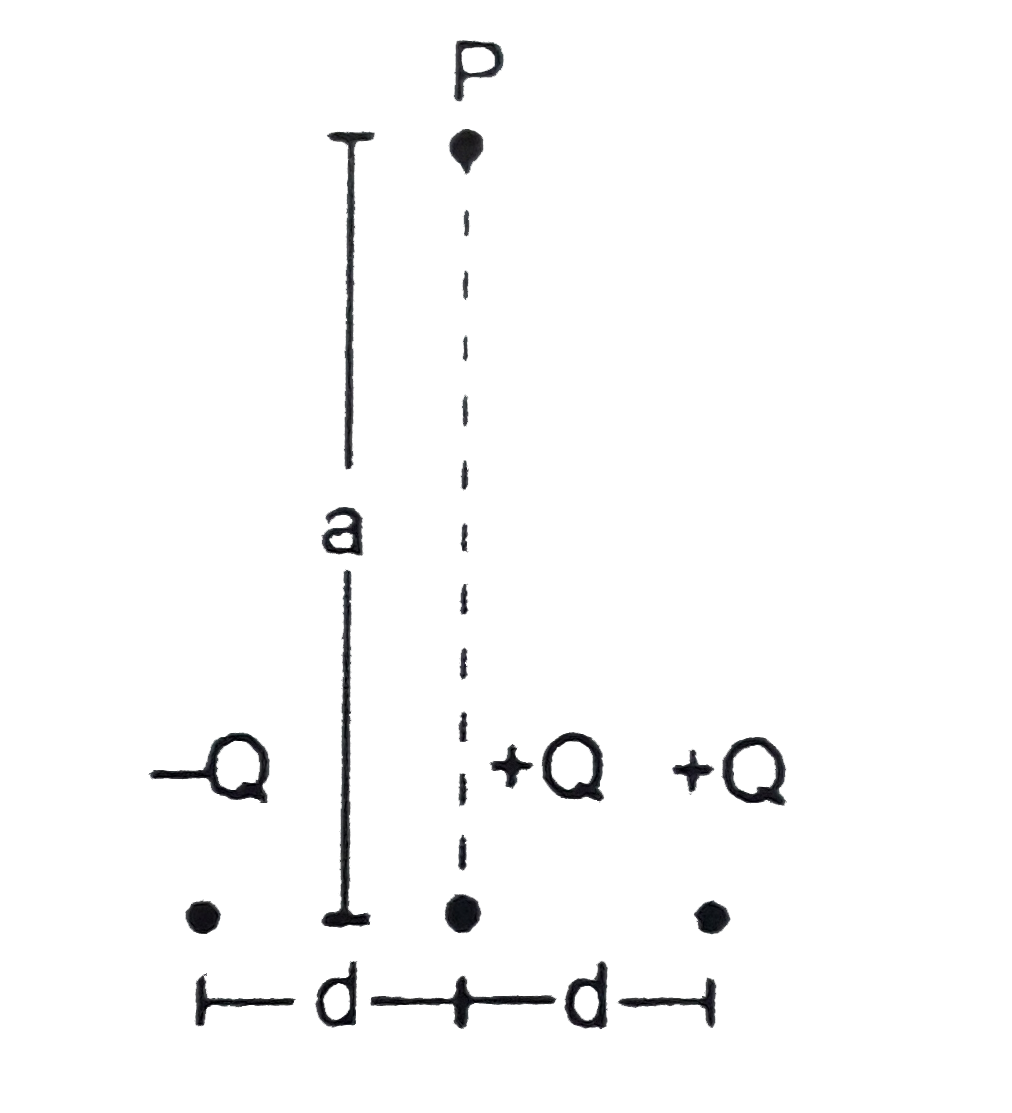
Three point charges -Q, Q and Q are placed on a straight line with distance d between charges as shown. Find the magnitude of the electric field at the point P in the configuration shown which is at a distance a from middle charge Q in the system provided that a>>d. Take 2Qd=p.
View SolutionTwo point charges q and -q are separated by a distance 2a. Evaluate the flux of the electric field strength vector across a circle of radius R.

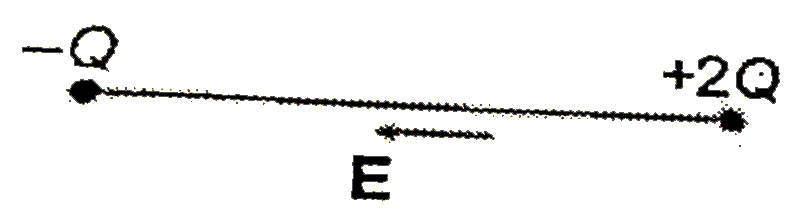
View SolutionCharge +2Q and −Q are placed as shown in figure.
The point at which electric field intensit is zero will be
View SolutionTwo point charges q and −q are separated by the distance 2l. Find the flux of the electric field strength vector across a circle of radius R.

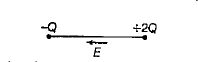
View SolutionCharges +2Q and −Q are placed as shown in figure. The point at which electric field intensity is zero will be
View Solution

