A light ray is incident by grazing one of the face of a prism and after refraction ray does not emerge out, what should be the angle of prism while critical angle is C ?
Equal to 2C
Less than 2C
More than 2C
None of the above
The correct Answer is:C
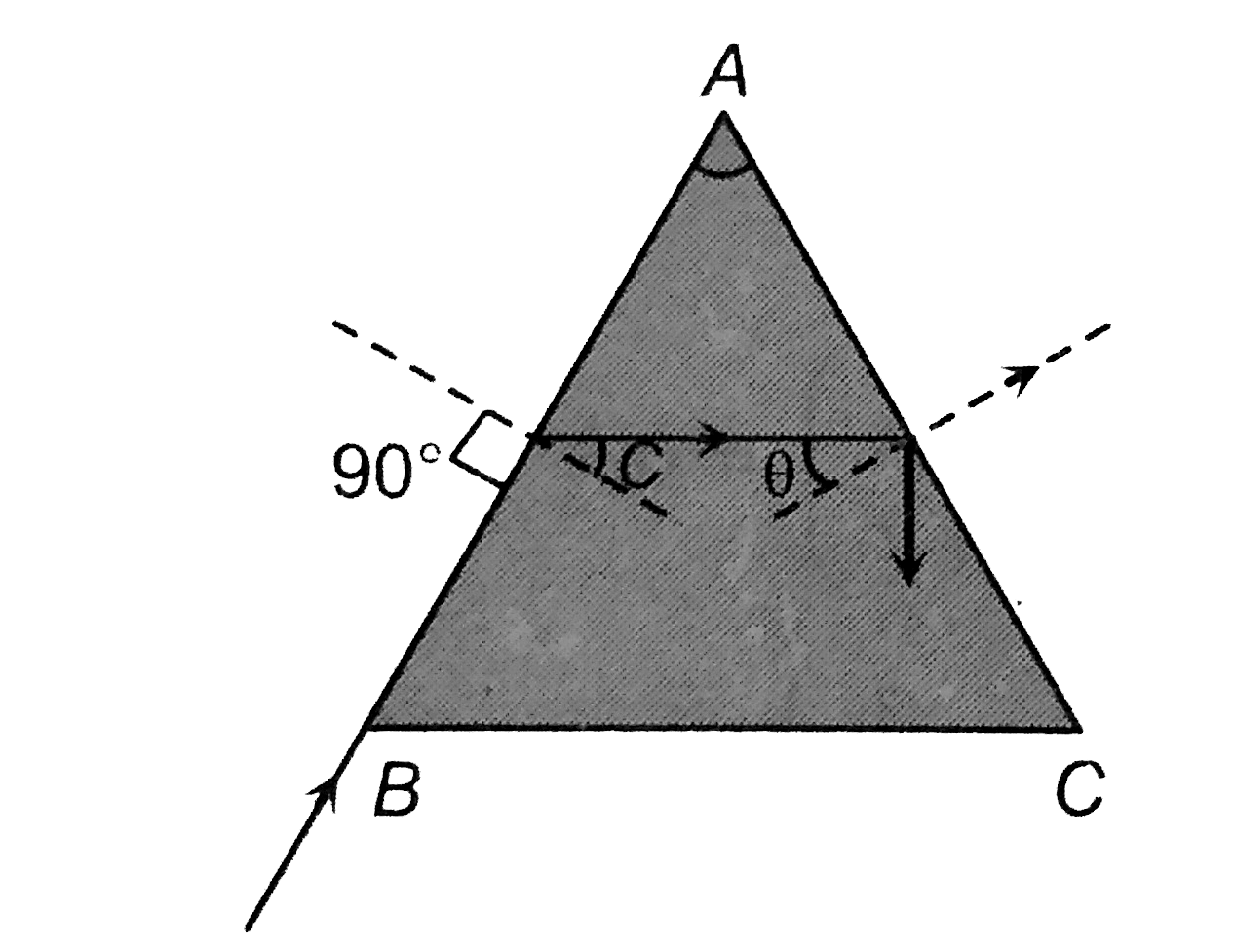
From any diagram
A=C+θ for TIR at AC
θ>C soA>AC
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:A2ZChapter:GEOMETRICAL OPTICSExercise:Optical Instruments
Explore 55 Videos
- GEOMETRICAL OPTICSBook:A2ZChapter:GEOMETRICAL OPTICSExercise:Problems Based On Mixed Concepts
Explore 37 Videos
- GEOMETRICAL OPTICSBook:A2ZChapter:GEOMETRICAL OPTICSExercise:Refraction At Curved Surface
Explore 64 Videos
- ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM Book:A2ZChapter:ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM Exercise:Section D - Chapter End Test
Explore 30 Videos
- MAGNETISM AND MATTERBook:A2ZChapter:MAGNETISM AND MATTERExercise:Section D - Chapter End Test
Explore 30 Videos
Similar Questions
A ray of light is incident at an angle of 60∘ on the face of a prism having refracting angle 30∘. The ray emerging out of the prism makes an angle 30∘ with the incident ray. Show that the emergent ray is perpendicular to the face through which it emerges.
View SolutionA ray of light is incident at an angle of 60∘ on the face of a prism having refracting angle 30∘. The ray emerging out of the prism makes an angle 30∘ with the incident ray. Show that the emergent ray is perpendicular to the face through which it emerges and calculate the refractive index of the material of prism.
View Solution
Knowledge Check
If a light ray incidents normally on one of the faces of the prism of refractive index 2 and the emergent ray just grazes the second face of the prism, then the angle of deviation is
A0∘B30∘C45∘D60∘
A ray of light incident on one of the face of a prism as shown. After refraction through this surface ray is incident on base of the prism. The refractive index of the prism is √3. The net deviation of the ray due to prism isA60∘ clockwiseB104∘ clockwiseC104∘ anticlockwiseD166∘ clockwiseA light ray is incident normally on one of the refracting faces of a prism and just emerges out grazing the second surface. Then, the relation between angle of the prism and its critical angle is
AA = CBA≠CCA<CDA>C
A ray of light incident normally on the first face of a glass prism of refractive index 1.6 just emerges from the other face. Find the angle of the prism.
View SolutionA ray of light is incident at an angle of 60∘ on one face of a prism which has refracting angle of 30∘ . The ray emerging out of the prism makes an angle of 30∘ with the incident ray. If the refractive index of the material of the prism is μ=√a , find the value of a .
View SolutionA monochromatic ray of light is incident normally on one of the refracting surfaces of a prism . The emergent ray grazes the second refracting surface . What is the angle of the prism if the refractive index of the material of the prism is 1.6 ?
View SolutionA ray of light is incident at an angle of 60∘ on one face of a prism of angle 30∘. They ray emerges normally from the other face of the prism. The refractive index of the prism material is
View SolutionA ray of monochromatic light is incident on one refracting face of a prism of refracting angle75∘ . It passes through the prism and is incident on the other face at the critical angle If the refracive index of the material of prism is √2, the angle of incidence on the first face o the prism is
View Solution

