Question

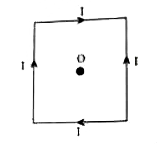
A wire in the from of a square of side $\text{'}a\text{'}$ carries a current $i$. Then the magnetic induction at the centre of the square wire is (Magnetic permeability of free space=${\mu }_0$)

Options

A. `(mu_(0)i)/(2pia)`
B. `(mu_(0)isqrt(2))/(pia)`
C. `(2sqrt(2)mu_(0)i)/(pia)`
D. `(mu_(0)i)/(sqrt(2)pia)`

Answer

C

Explanation

To find the magnetic induction at the center of a square wire carrying a current $$i$$, we can follow these steps:

Step 1: Understand the Geometry
We have a square wire with each side of length \( a \). The current \( i \) flows through the wire. The center of the square is equidistant from all four sides.

Step 2: Apply Biot-Savart Law
The magnetic field \( B \) at a point due to a small segment of wire carrying current can be calculated using the Biot-Savart law:
\( B = \frac{\mu_0}{4\pi} \frac{i \, dL \times \hat{r}}{r^2} \)
where \( dL \) is the current element, \( \hat{r} \) is the unit vector from the current element to the point where the field is being calculated, and \( r \) is the distance from the current element to that point.

Step 3: Calculate Contribution from One Side
For one side of the square (let's say side AB), the distance from the center to the wire is \( \frac{a}{2} \). The angle between the wire and the line connecting the wire to the center is \( 45^\circ \).

Using the Biot-Savart law, the magnetic field \( B_{AB} \) at the center due to one side (AB) can be calculated as:
\( B_{AB} = \frac{\mu_0}{4\pi} \frac{i}{\frac{a}{2}} \left( \sin(45^\circ) + \sin(45^\circ) \right) \)
Since \( \sin(45^\circ) = \frac{1}{\sqrt{2}} \):
\( B_{AB} = \frac{\mu_0}{4\pi} \frac{i}{\frac{a}{2}} \left( \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} \right) = \frac{\mu_0}{4\pi} \frac{i}{\frac{a}{2}} \cdot \frac{2}{\sqrt{2}} = \frac{\mu_0 i}{2\pi a} \cdot \frac{1}{\sqrt{2}} \)

Step 4: Total Contribution from All Sides
Since the square is symmetric, the magnetic field contributions from all four sides will be the same in magnitude. Therefore, the total magnetic field \( B \) at the center is:
\( B = 4 \cdot B_{AB} = 4 \cdot \left( \frac{\mu_0 i}{2\pi a \sqrt{2}} \right) = \frac{2\sqrt{2} \mu_0 i}{\pi a} \)

Step 5: Conclusion
Thus, the magnetic induction at the center of the square wire is:
\( B = \frac{2\sqrt{2} \mu_0 i}{\pi a} \)