A wire carrying current I and other carrying 2I in the sam direction produce a magnetic field B at the midpoint. What will be the field when 2I wire is swiched off?
B/2
2B
B
4B
The correct Answer is:C
To solve the problem step by step, we will analyze the magnetic fields produced by the two wires at the midpoint and then determine the effect of switching off the current in the second wire.
Step 1: Understand the Setup
We have two parallel wires:
- Wire 1 carries current I.
- Wire 2 carries current 2I.
Both currents flow in the same direction.
Step 2: Magnetic Field due to Each Wire
The magnetic field B produced by a long straight wire carrying current I at a distance r from the wire is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
Step 3: Calculate Magnetic Field at Midpoint
Let’s denote the distance from each wire to the midpoint as r.
- The magnetic field due to wire 1 (current I) at the midpoint is:
B1=μ0I2πr
- The magnetic field due to wire 2 (current 2I) at the midpoint is:
B2=μ0(2I)2πr=μ0Iπr
Step 4: Determine the Net Magnetic Field
Since both currents are in the same direction, the magnetic fields produced by each wire at the midpoint will add up:
Bnet=B1+B2=μ0I2πr+μ0Iπr
To combine these, we can express B2 with a common denominator:
Bnet=μ0I2πr+2μ0I2πr=3μ0I2πr
Step 5: Effect of Switching Off the Second Wire
When we switch off the current in the second wire (current 2I), only the first wire (current I) will contribute to the magnetic field at the midpoint. Thus, the magnetic field will be:
B′=B1=μ0I2πr
Step 6: Relate B′ to B
From our earlier calculations, we found that:
B=3μ0I2πr
Now, we can express B′ in terms of B:
B′=μ0I2πr=13B
Conclusion
When the wire carrying current 2I is switched off, the magnetic field at the midpoint will be one-third of the original magnetic field B produced by both wires.
Final Answer
The magnetic field when the wire carrying 2I is switched off is 13B.
---
We have two parallel wires:
- Wire 1 carries current I.
- Wire 2 carries current 2I.
Both currents flow in the same direction.
The magnetic field B produced by a long straight wire carrying current I at a distance r from the wire is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
Let’s denote the distance from each wire to the midpoint as r.
- The magnetic field due to wire 1 (current I) at the midpoint is:
B1=μ0I2πr
- The magnetic field due to wire 2 (current 2I) at the midpoint is:
B2=μ0(2I)2πr=μ0Iπr
Since both currents are in the same direction, the magnetic fields produced by each wire at the midpoint will add up:
Bnet=B1+B2=μ0I2πr+μ0Iπr
To combine these, we can express B2 with a common denominator:
Bnet=μ0I2πr+2μ0I2πr=3μ0I2πr
When we switch off the current in the second wire (current 2I), only the first wire (current I) will contribute to the magnetic field at the midpoint. Thus, the magnetic field will be:
B′=B1=μ0I2πr
From our earlier calculations, we found that:
B=3μ0I2πr
Now, we can express B′ in terms of B:
B′=μ0I2πr=13B
When the wire carrying current 2I is switched off, the magnetic field at the midpoint will be one-third of the original magnetic field B produced by both wires.
The magnetic field when the wire carrying 2I is switched off is 13B.
Topper's Solved these Questions
- SOURCE AND EFFECT OF MAGNETIC FIELDBook:A2ZChapter:SOURCE AND EFFECT OF MAGNETIC FIELDExercise:Magnetic Field Due To Circular Arc
Explore 69 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBook:A2ZChapter:SOURCE AND EFFECT OF MAGNETIC FIELDExercise:Problems Based On Mixed Concepts
Explore 32 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBook:A2ZChapter:SOURCE AND EFFECT OF MAGNETIC FIELDExercise:Magnetic Dipole
Explore 32 Videos
- SEMICONDUCTOR ELECTRONICSBook:A2ZChapter:SEMICONDUCTOR ELECTRONICSExercise:EXERCISE
Explore 29 Videos
- WAVE OPTICSBook:A2ZChapter:WAVE OPTICSExercise:Section D - Chapter End Test
Explore 29 Videos
Similar Questions
A conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be

View SolutionTwo parallel, long wires carry current i1 and i2 withi1>i2. When the currents are in the same direction, the magnetic field at a point midway between the wires is 30μT. If the direction of i1 is reversed , the field becomes 90μT. The ratio i1/i2 is
View Solution
Knowledge Check
Two parallel wires carrying current I and 2I in same direction have magnetic field B at the midpoint between them. If the current 2I is switched off, the magnetic field at that point will be
AB/2BBC2BD3BTwo parallel, long wires carry currents t1andt2 with t1>t2. When the currents are in the same direction, the magnetic field at a point midway between the wires is 10 μT. If the direction of i2 is reversed, the field becomes 30 μT. Find the ratio i1i2.
A4B3C2D1Two parallel long wires carry currents i1 and i2 with i1>i2 .When the current are in the same direction, the magnetic field at a point midway between the wire is 20μT.If the direction of i1,is reversed.the field becomes 30μT.The ratio i1/i2 is
A4B3C5D1
Two long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
View SolutionTwo long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
View SolutionA long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is

View SolutionTwo long parallel straight conductors carry currents 7, and 12 (I1>I2) When the currents are in the same direction, the magnetic field at a point midway between the wires is 20 mt. If the direction of Iz is reversed, the field becomes 50 mt. The ratio of the currents
View SolutionA wire carrying current i is shaped as shown. Section AB is a quarter circle of radius r. The magnetic field is directed
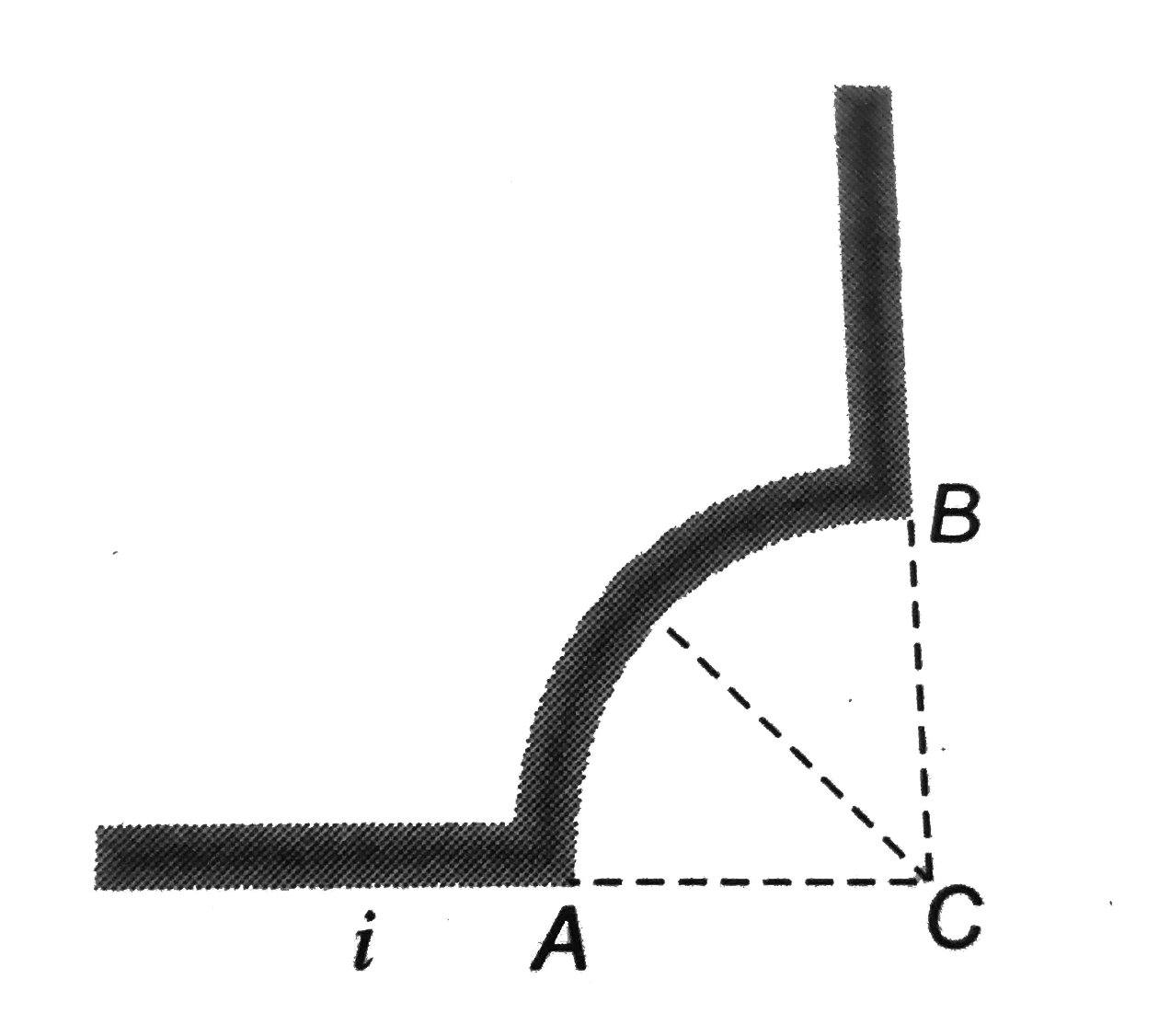
View Solution

