Two infinitely long parallel wires having linear charge densities λ1 and λ2 respectively are placed at a distance of R metres. The force per unit length on either wire will be (k=14πε0)
k2λ1λ2R2
k2λ1λ2R
kλ1λ2R2
kλ1λ2R
The correct Answer is:B
To solve the problem of finding the force per unit length between two infinitely long parallel wires with linear charge densities λ1 and λ2 separated by a distance R, we can follow these steps:
1. Understand the Setup:
We have two infinitely long parallel wires. Wire 1 has a linear charge density λ1 and wire 2 has a linear charge density λ2. The distance between the two wires is R.
2. Determine the Charge on a Length of Wire:
Consider a segment of length L of wire 2. The total charge Q on this segment can be calculated as:
Q=λ2⋅L
3. Calculate the Electric Field due to Wire 1:
The electric field E produced by an infinitely long wire with linear charge density λ1 at a distance R from the wire is given by:
E=12πϵ0⋅λ1R
Here, ϵ0 is the permittivity of free space.
4. Substitute K into the Electric Field Expression:
We know that k=14πϵ0. Therefore, we can express ϵ0 in terms of k:
ϵ0=14πk
Substituting this into the electric field expression gives:
E=λ12πϵ0R=2kλ1R
5. Calculate the Force on Wire 2:
The force F on wire 2 due to the electric field E created by wire 1 is given by:
F=Q⋅E=(λ2⋅L)⋅(2kλ1R)
Simplifying this gives:
F=2kλ1λ2LR
6. Find the Force per Unit Length:
To find the force per unit length f, we divide the total force F by the length L:
f=FL=2kλ1λ2LR⋅L=2kλ1λ2R
Final Answer:
The force per unit length on either wire is given by:
f=2kλ1λ2R
We have two infinitely long parallel wires. Wire 1 has a linear charge density λ1 and wire 2 has a linear charge density λ2. The distance between the two wires is R.
Consider a segment of length L of wire 2. The total charge Q on this segment can be calculated as:
Q=λ2⋅L
The electric field E produced by an infinitely long wire with linear charge density λ1 at a distance R from the wire is given by:
E=12πϵ0⋅λ1R
Here, ϵ0 is the permittivity of free space.
We know that k=14πϵ0. Therefore, we can express ϵ0 in terms of k:
ϵ0=14πk
Substituting this into the electric field expression gives:
E=λ12πϵ0R=2kλ1R
The force F on wire 2 due to the electric field E created by wire 1 is given by:
F=Q⋅E=(λ2⋅L)⋅(2kλ1R)
Simplifying this gives:
F=2kλ1λ2LR
To find the force per unit length f, we divide the total force F by the length L:
f=FL=2kλ1λ2LR⋅L=2kλ1λ2R
The force per unit length on either wire is given by:
f=2kλ1λ2R
Topper's Solved these Questions
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section B - Assertion Reasoning
25 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - AIPMTNEET Questions
24 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Dipole
29 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
Two infinitely long parallel wires having linear charge density 3×10−9 C/m and 4×10−9 C/m are kept at a distance of 20 cm in air. What will be the magnitude and direction of the electric field intensity at a point that is at a distance of 10 cm from each wire?
View SolutionBetween two infinitely long wires having linear charge densities λ and −λ there are two points A and B shown in the figure. The amount of work done by the electric field moving a point charge q0 from A to B is equal to
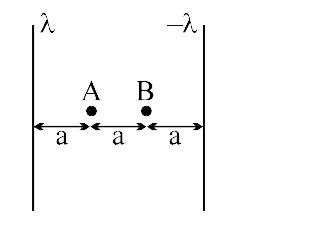
View Solution
Knowledge Check
When two parallel wires carrying current l and 2l in same direction are placed at a distance d apart, the ratio of force per unit length acting upon the wire due to other is
A1:1B1:2C2:1DNone of theseTwo parallel infinite line charges with linear charge densities +λC/m and −λ C/m are placed at a distance of 2R in free space. What is the electric field mid-way between the two line charges?
Aλ2πε0RN/CBzeroC2λπε0RN/CDλπε0RN/CTwo infinitely long thin styraight wires having uniform linear charge densities λ and 2λ are arranged parallel to each other at a distance r apart.The intensity of the electric field at a point midway between them is
A2λπε0Bλπε0rCλ2πε0rD3λ2πε0r
Two parallel wires carrying current 1 A and 3 A respectively are 1 m apart. If the current is in opposite direction, the force per unit length on both the wires will be:
View SolutionThe electric field at a distance r from a long wire having charge per unit length λ is
View SolutionTwo uniformly long charged wires with linear densities λ and 3λ are placed along X and Y axis respectively. Determined the slope of electric field at any point on the l ine y=√3x
View SolutionTwo long parallel copper wires carry current of 5A each in opposite directions. If the wires are separated by a distance distance of 0.5m, then the force per unit length between the two wires is
View SolutionBetween two infinitely long wires having linear charge densities λ and −λ , there are two points A and B as shown in the figure. The amount of work done by the electric field in moving a point charge q0 from A to B is equal to :

View Solution
