If →E=E0Xaˆi(x−mt) then flux through the shaded area is:
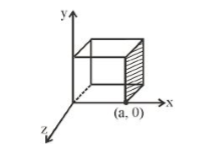
E0a2
Zero
E0a3
−E0a3
The correct Answer is:A
φ=∫→E.d→A
=∫E0aadA
=E0∫dA=E0a2
πJ0R=∫R0dr
πJ0Y=Ryπ=πR3J0J04R
Topper's Solved these Questions
Similar Questions
consider a uniform electric field →E=3×103ˆiN/C
What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane?
(b) What is the flux through the same square if if the normal to its plane makes a 60∘ angle with the x-axis?
View SolutionGiven a uniform electric field →E=5×103ˆiN/C, find the flux of this field through a square of 10cm on a side whose plane is parallel to the y - z plane. What would be the flux through the same square if the plane makes a 30∘ angle with the x-axis?
View Solution
Knowledge Check
Conisder an electric field →E=E0ˆx where E0 is a constant .
The flux through the shaded area (as shown in the figure) due to this field is
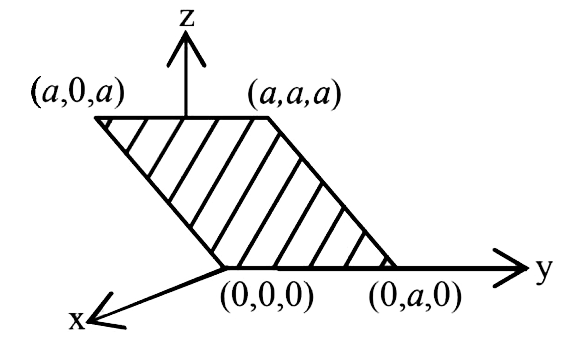 A(a) 2E0a2B(b) √2E0a2C(c) E0a2D(d) E0a2√2
A(a) 2E0a2B(b) √2E0a2C(c) E0a2D(d) E0a2√2If →E=35ˆi+45ˆj then find electric flux through an area of 0.4 m^2 parallel to y-z plane
A0.12Nm2CB0.24Nm2CC0.36Nm2CD0.48Nm2CGiven : →E=(10ˆi+7ˆj)Vm−1. The electric flux through 1m2 area is XZ plane is
A10 VmB7VmC100 VmD49Vm
The electric field componets due to a charge inside the cube of side 0.1m are Ex=αx, where α=500(N/C)m−1,
Ey=0,Ez=0. Calculate the flux through the cube and the charge inside the cube.
View SolutionGiven a uniform electric field →E=5×103ˆiNC−1 . Find the flux of this field through square of 10 cm on a side whose plane is parallel to the y-Z plane.
What would be the flux through the same square if the plane makes a 30∘ angle with the x-axis?
View SolutionGiven a uniform electric field →E=5×103ˆiN/C, find the flux of this field through a square of 10cm on a side whose plane is parallel to the y - z plane. What would be the flux through the same square if the plane makes a 30∘ angle with the x-axis?
View SolutionA uniform electric field →E=aˆi+bˆj intersects a surface of area A .What is the flux through this area if the surface lies in the yz plane?
View SolutionA cylinder of length L and radius b has its axis coincident with x-axis. The electric field in this region is →E=200ˆi. Find the flux through the left end of the cylinder.
View Solution

