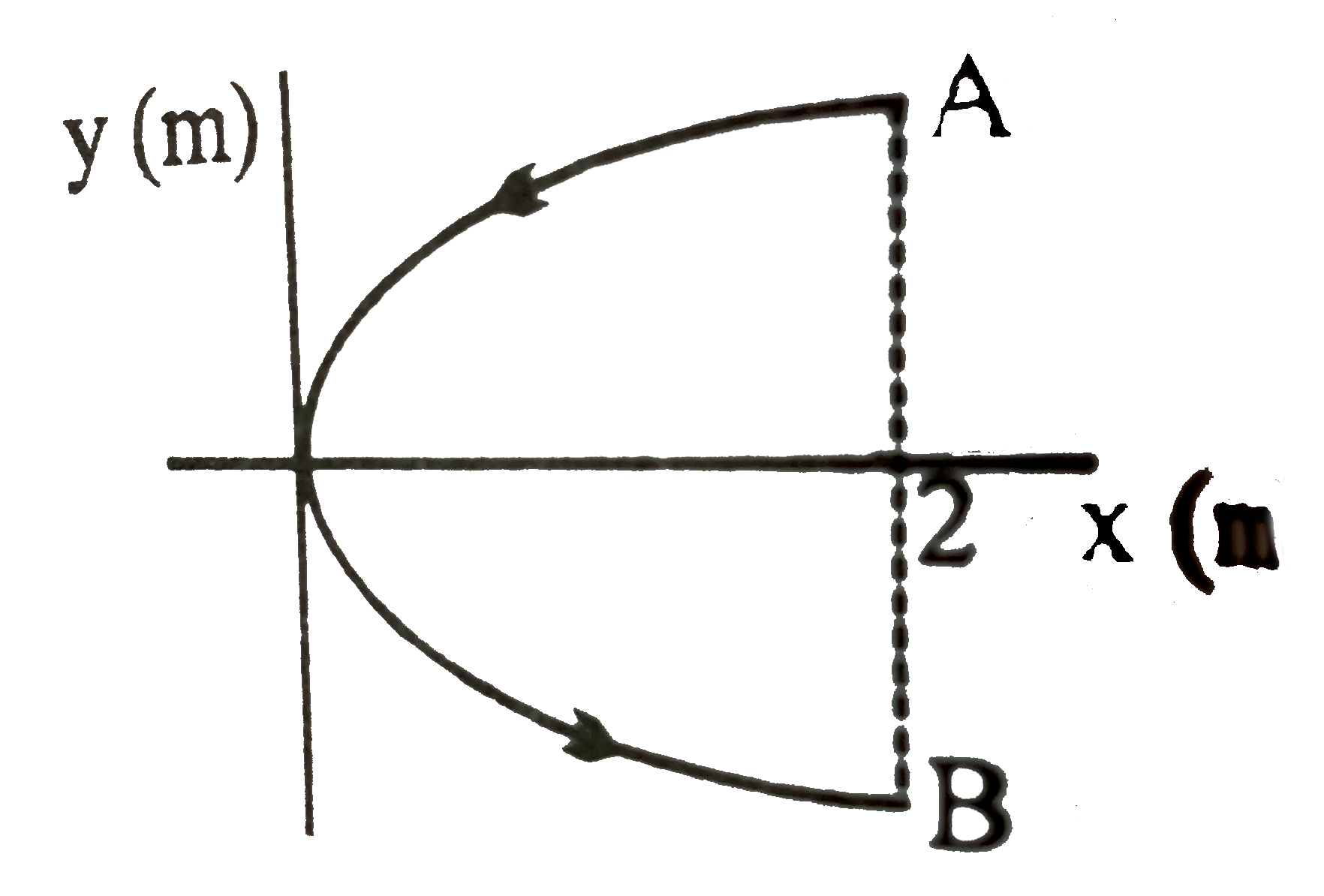
A conducting wire is bend into a loop as shown in the figure. The segment AOB is parabolic given by the equation y2=2x, while segment BA is a straight line x = 2. the magnrtic field in the region →B=−8ˆk tesla and the current in wire is 2A.

If the loop were rotated about the z-axis with an angular speed of 1 rad/sec. Then magnitude of emf induced across the straight segment AC will be
32V
8V
16V
4V
The emf is the difference between emf across straight segment OA and OC.
Topper's Solved these Questions
Similar Questions
A conducting wire is bent into a loop as shown in the figure. The segment AOB is parabolic given by the equation y2=2x while segment BA is a straight line parallel to the y-axis. The magnetic field in the region is →B−8ˆk and the current in the wire is 2A.
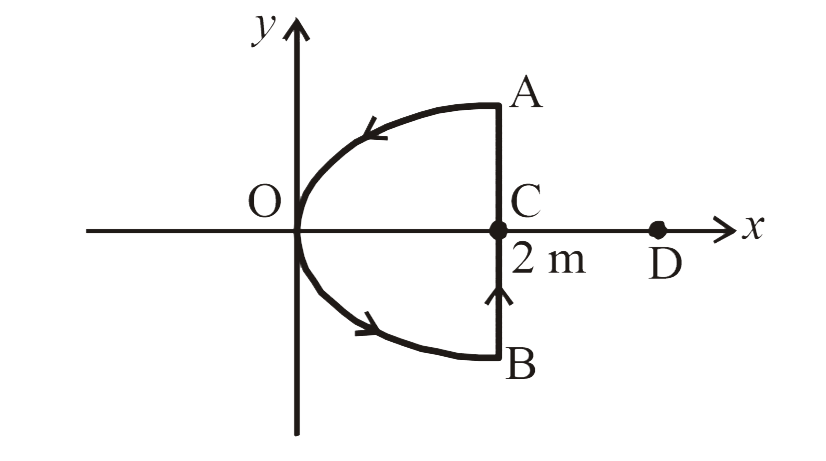
The torque on the loop will be
View SolutionA conducting wire is bent into a loop as shown in the figure. The segment AOB is parabolic given by the equation y2=2x while segment BA is a straight line parallel to the y-axis. The magnetic field in the region is →B−8ˆk and the current in the wire is 2A.
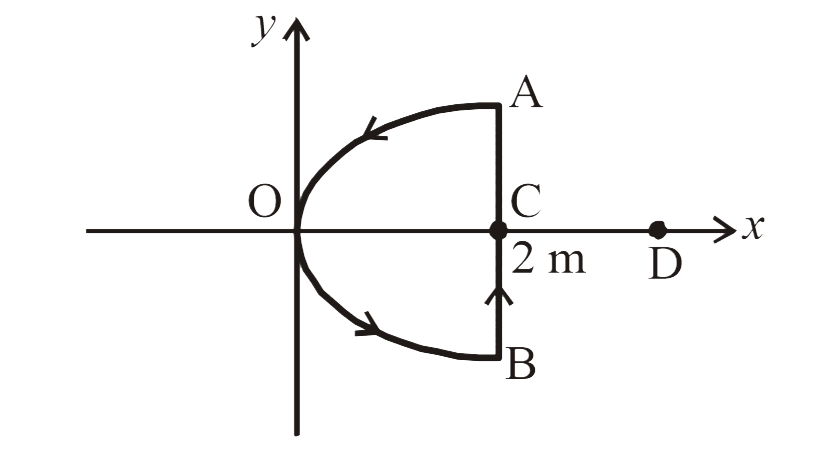
The field created by the current in the loop at point C will be
View Solution
Knowledge Check
A conducting wire is bend into a loop as shown in the figure. The segment AOB is parabolic given by the equation y2=2x, while segment BA is a straight line x = 2. the magnrtic field in the region →B=−8ˆk tesla and the current in wire is 2A.
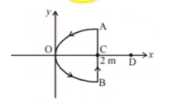
The magnetic field created by the current in the loop at point C will beA−μ04πˆkB−μ08πˆkC−μ0√2πˆkDnoneAn irregular loop of conducting wire is lying on a frictionless table as shown in the figure. The wire is clamped at points a and k, when a current i is passed thorugh it, then the wire will
 Abecomes parallel in two partsBcollapse moreCform a circular loopDnone of these
Abecomes parallel in two partsBcollapse moreCform a circular loopDnone of theseA non - planar loop of conducting wire carrying a current I is placed as shown in the figure . Each of the straighrt sections of the loop is of the length 2a. The magnetic field due to this loop at the point P(a,0,a) points in the direction
 A1√2(−ˆj+ˆk)B1√3(−ˆj+ˆk+ˆi)C1√3(ˆi+ˆj+ˆk)D1√2(ˆi+ˆk)
A1√2(−ˆj+ˆk)B1√3(−ˆj+ˆk+ˆi)C1√3(ˆi+ˆj+ˆk)D1√2(ˆi+ˆk)
A conducting wire is bent into a loop as shown in the figure. The segment AOB is parabolic given by the equation y2=2x while segment BA is a straight line parallel to the y-axis. The magnetic field in the region is →B−8ˆk and the current in the wire is 2A.
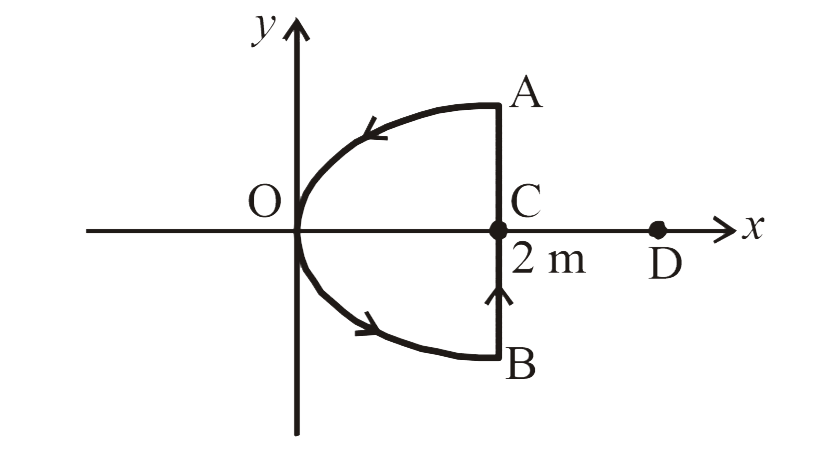
Magnetic field at point D due to segment AO of the loop is directed parallel to
View SolutionA rectangular loop is placed near a current carrying straight wire as shown in the figure. If the loop is rotated about an axis passing throught one of its sides find the direction of induced current in the loop.
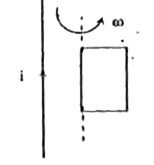
View SolutionA rectangular loop is placed adjacent toa current carrying straight wire as shown in Figure. If the loop is rotated about an axis passing through one of its sides find the direction of induced current in the loop.

View SolutionA non-planar loop of conducting wire carrying a current 1 is placed as shown in the figure. Each of the straight sections of the loop is of length 2a. The magnetic field due to this loop at the point P (a,0, ) points in the direction

View SolutionA conducting wire bent in the from of a parabola y2=2x carries a current i=2A as shown in figure This wire is placed in a unifrom magnetic field
→B=−4ˆk Tesla The magnetic force on the wire is (newton)
 .
.
View Solution

