A conducting wire is bent into a loop as shown in the figure. The segment AOB is parabolic given by the equation y2=2x while segment BA is a straight line parallel to the y-axis. The magnetic field in the region is →B−8ˆk and the current in the wire is 2A.
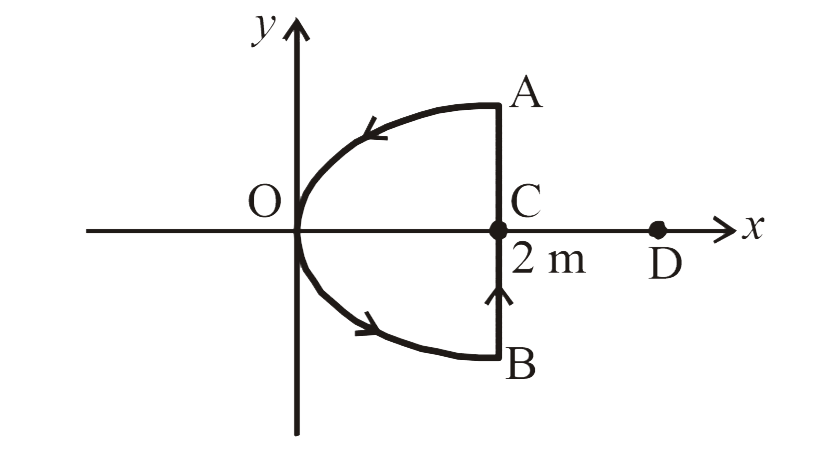
Magnetic field at point D due to segment AO of the loop is directed parallel to
ˆk
−ˆk
ˆi
ˆj
Step by step video & image solution for A conducting wire is bent into a loop as shown in the figure. The segment AOB is parabolic given by the equation y^(2) =2x while segment BA is a straight line parallel to the y-axis. The magnetic field in the region is vec(B) - 8 hat(k) and the current in the wire is 2A. Magnetic field at point D due to segment AO of the loop is directed parallel to by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A conducting wire is bent into a loop as shown in the figure. The segment AOB is parabolic given by the equation y2=2x while segment BA is a straight line parallel to the y-axis. The magnetic field in the region is →B−8ˆk and the current in the wire is 2A.
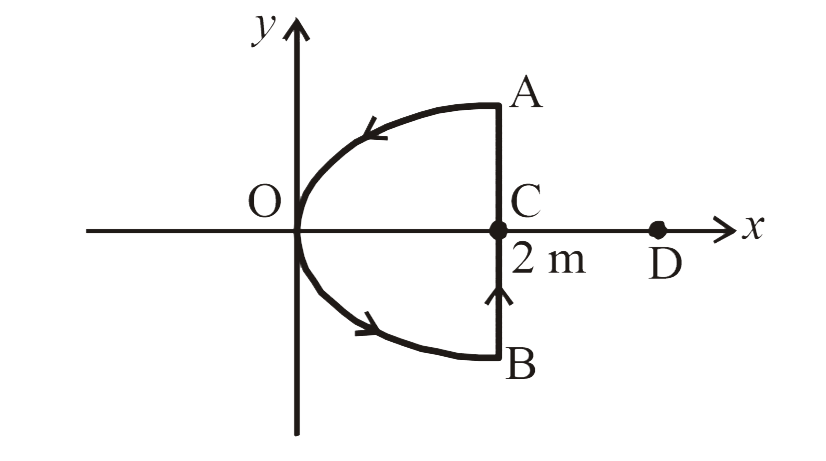
The torque on the loop will be
View SolutionA conducting wire is bent into a loop as shown in the figure. The segment AOB is parabolic given by the equation y2=2x while segment BA is a straight line parallel to the y-axis. The magnetic field in the region is →B−8ˆk and the current in the wire is 2A.
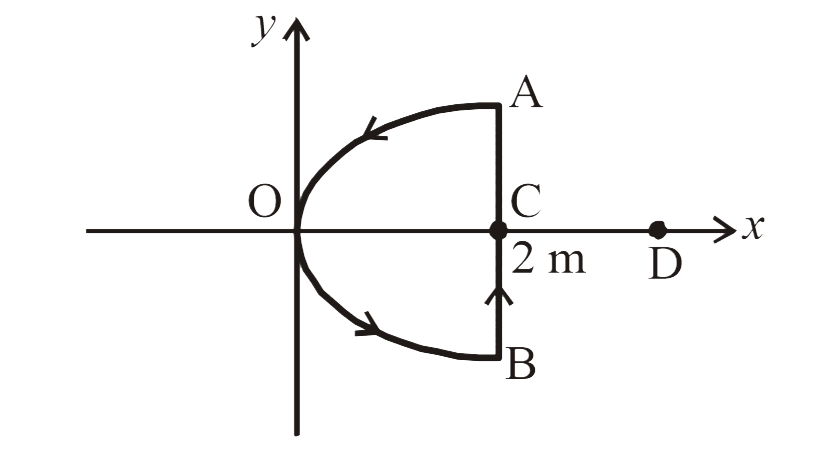
The field created by the current in the loop at point C will be
View Solution
Knowledge Check
A conducting wire is bend into a loop as shown in the figure. The segment AOB is parabolic given by the equation y2=2x, while segment BA is a straight line x = 2. the magnrtic field in the region →B=−8ˆk tesla and the current in wire is 2A.
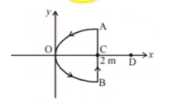
The magnetic field created by the current in the loop at point C will beA−μ04πˆkB−μ08πˆkC−μ0√2πˆkDnoneA conducting wire is bend into a loop as shown in the figure. The segment AOB is parabolic given by the equation y2=2x, while segment BA is a straight line x = 2. the magnrtic field in the region →B=−8ˆk tesla and the current in wire is 2A.

If the loop were rotated about the z-axis with an angular speed of 1 rad/sec. Then magnitude of emf induced across the straight segment AC will beA32VB8VC16VD4V
A conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be

View SolutionA straight conducting wire is bent as shown in the adjoining figure. Calculate the magnetic field at point O.

View SolutionB0 is the magnetic field at point P fir s given straight wire as shown in figure. If this wire is bent into a circular loop,then magnetic field at the center of the loop is
_PHY_E06_051_Q01.png)
View SolutionThe segment of wire shown in figure carries a current of i=5 A. The magnetic field (in Tesla) at the point P is

View SolutionA wire is placed parallel to the lines of force in a magnetic field and a current flows in the wire. Then :
View SolutionA current is passed through a straight wire bent at a point. The magnetic field established around it has its lines offorces :
View Solution
