One has to throw a particle from one side of a fixed sphere, in a diameterical plane to another side such that it just grazes the sphere. Minimum possible speed for this is $\sqrt{2 g R (\sqrt{α} + \sqrt{β})}$ . Find $α + β$

Video Solution

Text Solution

Verified by Experts

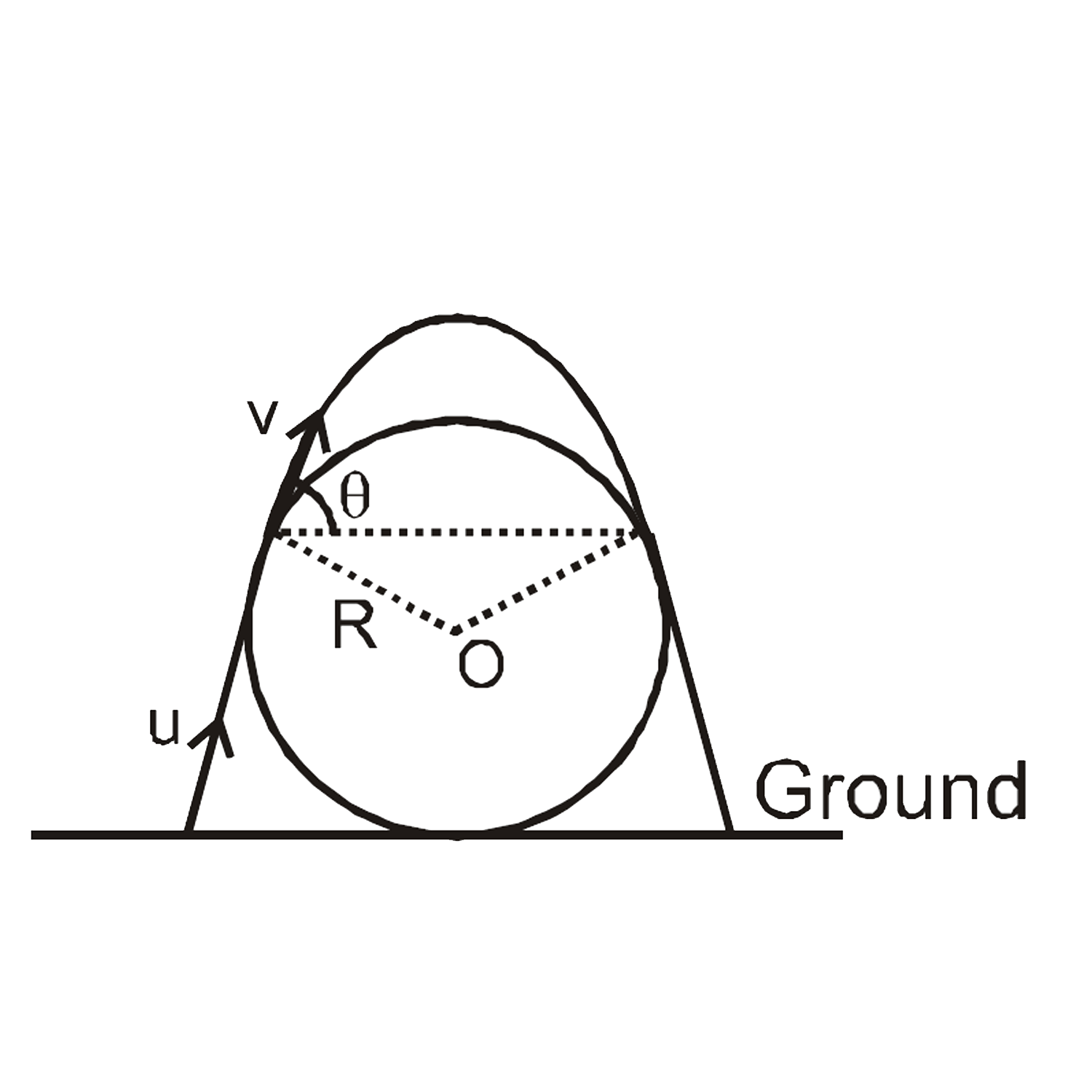
$\frac{2 V^{2} sin θ cos θ}{g} = 2 R sin θ \Rightarrow v^{2} = \frac{R g}{cos θ}$
$u^{2} = V^{2} + 2 g R (1 + cos θ)$
$u^{2} = \frac{R g}{cos θ} + 2 g R + 2 g R cos θ$
$u^{2} = R \frac{g (1 + 2 {cos}^{2} g)}{cos θ} + 2 g R$
for $u$ to be minimum $\frac{1 + 2 {cos}^{2} θ}{cos θ} = min$
$\Rightarrow cos θ = \frac{1}{\sqrt{2}} \Rightarrow θ = π / 4$
$u_{min} = \sqrt{\sqrt{2 R g} + 2 g R + \sqrt{2} R g} = \sqrt{2 g R (\sqrt{2} + 1)}$

Updated on:21/07/2023

If the quadratic equation $x^{2} - 36 x + λ = 0$ has roots $α$ and $β$ such that $α$ , $β \in N$ and (lambda)/(5) cancel in Z and $λ$ assumes minimum possible value then $\frac{\sqrt{α + 2} \sqrt{β + 2}}{| α - β |}$ is equal to
A $\frac{3}{8}$
B $\frac{3}{16}$
C $\frac{\sqrt{111}}{34}$
D $\frac{\sqrt{111}}{17}$
$If \int \frac{1}{\sqrt{4 x^{2} - 5}} d x = α log ∣ ∣ ∣ x + \sqrt{x^{2} - β} ∣ ∣ ∣, then α + 2 β$ is
A $- 2$
B2
C $- 3$
D3