Aray of light falls on one side of a prism whose refracting angle is 75∘. Find the angle of incidence in order that the emergent ray may just graze the other side, (μ=√2)
To solve the problem, we need to find the angle of incidence (I) for a ray of light falling on a prism with a refracting angle of 75∘ such that the emergent ray just grazes the other side of the prism. The refractive index (μ) of the prism is given as √2.
1. Understanding the Geometry of the Prism:
- The prism has a refracting angle A=75∘.
- The ray of light enters the prism and refracts at the first surface (AB) and exits at the second surface (AC).
- The emergent ray just grazing the other side means it exits at an angle of 90∘ to the normal at surface AC.
2. Finding the Angle of Refraction at Surface AC:
- Since the emergent ray grazes the surface AC, the angle of refraction R2 at this surface is 90∘.
- Using the critical angle condition, we know that:
sinR2=1μ
- Given μ=√2:
sinR2=1√2⟹R2=45∘
3. Using the Prism Formula:
- The relationship between the angles in the prism is given by:
A=R1+R2
- Substituting the known values:
75∘=R1+45∘
- Solving for R1:
R1=75∘−45∘=30∘
4. Applying Snell's Law at the First Surface (AB):
- At the first surface, we apply Snell's Law:
μ1sinI=μ2sinR1
- Here, μ1=1 (for air) and μ2=√2:
1⋅sinI=√2⋅sin30∘
- Since sin30∘=12:
sinI=√2⋅12=√22
5. Finding the Angle of Incidence (I):
- Now, we find I:
I=sin−1(√22)
- This gives:
I=45∘
Final Answer:
The angle of incidence I required for the emergent ray to just graze the other side of the prism is 45∘.
- The prism has a refracting angle A=75∘.
- The ray of light enters the prism and refracts at the first surface (AB) and exits at the second surface (AC).
- The emergent ray just grazing the other side means it exits at an angle of 90∘ to the normal at surface AC.
- Since the emergent ray grazes the surface AC, the angle of refraction R2 at this surface is 90∘.
- Using the critical angle condition, we know that:
sinR2=1μ
- Given μ=√2:
sinR2=1√2⟹R2=45∘
- The relationship between the angles in the prism is given by:
A=R1+R2
- Substituting the known values:
75∘=R1+45∘
- Solving for R1:
R1=75∘−45∘=30∘
- At the first surface, we apply Snell's Law:
μ1sinI=μ2sinR1
- Here, μ1=1 (for air) and μ2=√2:
1⋅sinI=√2⋅sin30∘
- Since sin30∘=12:
sinI=√2⋅12=√22
- Now, we find I:
I=sin−1(√22)
- This gives:
I=45∘
The angle of incidence I required for the emergent ray to just graze the other side of the prism is 45∘.
Similar Questions
Calculate the angle of incidence on the face of a prism of refracting angle 60∘ and of refractive index 1.5, for which the emergent ray just grazes the other face.
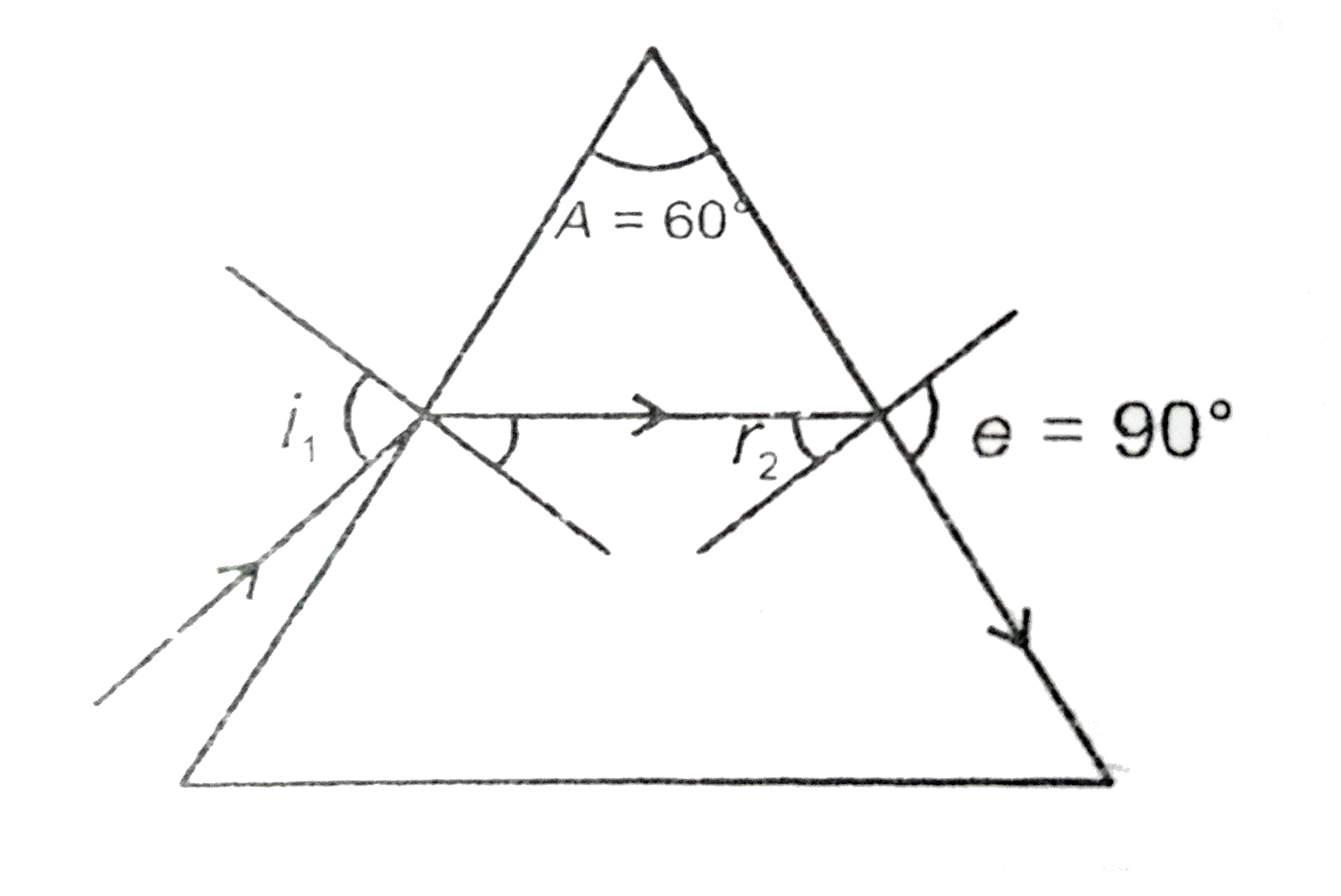
View SolutionA ray of light falls on a normally on a refracting face of a prism. Find the angle of prism if the ray just fails to emerge from the prism (μ=3/2).
View Solution
Knowledge Check
Light ray is incident on a prism of angle A=60∘ are refractive index μ=√2. The angle of incidence which the emergent rays grazes the surface is given
Asin−1(√3−12)Bsin−1(√2−12)Csin−1(√32)Dsin−1(23√3)Light ray is incident on a prism of angle A=60∘and refractive indexμ=√2.the angle of incidence at which the emergent ray grazes the surface is given by
Asin−1(√3−12)Bsin−1(1−√32)Csin−1(√32)Dsin−1(2√3)A ray of light takes grazing incidence on the first face of a prism having critical angle C. Find the angle of prism is after refraction ray does not emerge out.
AEqual to 2CBLess than 2CCMore than 2CDNone of the above
A prism of refractive index √2 has refractive angle 60∘ . Find the angle of incidence so that a ray minimum deviation.
View SolutionA ray of light enters the face AB of a glass prism of refractive index μ at an angle of incidence i. Find the value of i such that no ray emerges from the face AC of the prism, given angle of prism is A.
View SolutionA ray of light the face AB of a glass prism of refractive index μ at an angle of incidence i. Find the value of i such that no ray emerges from the face AC of the prism. Given angle of prism is A.
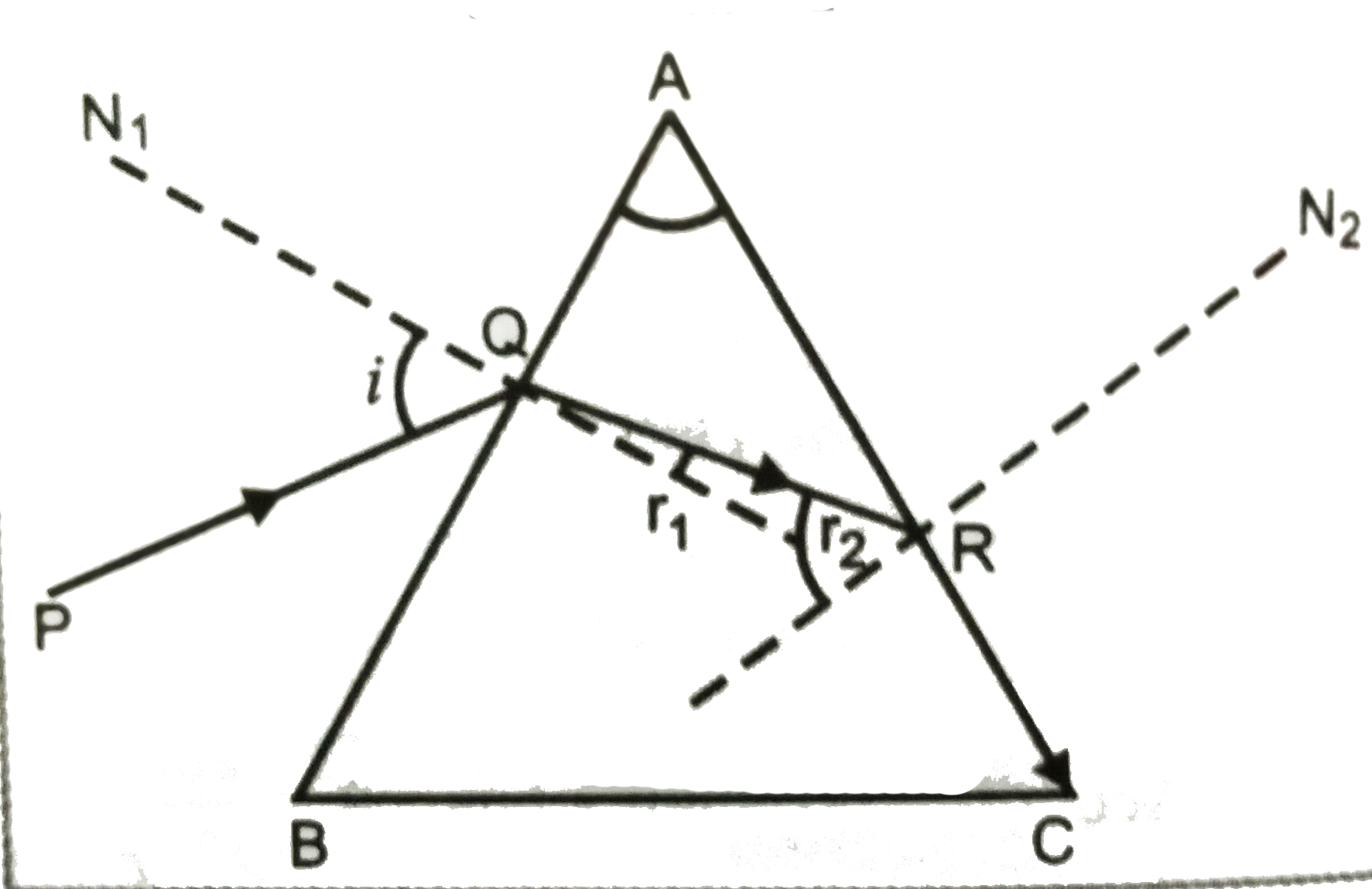
View SolutionA ray of light falls on a glass prism at a angle of incidence of 30∘. Find the direction of the emergent ray if the angle of the prism is 60∘ and refractive index is 1.50
View SolutionFor a ray of light refracted through a prism of angle 60∘, the angle of incidence is equal to the angle of emergence, each equal to 45∘. Find the refractive index of the material of the prism.
View Solution

