Position (in m) of a particle moving on a straight line varies with time (in sec) as x=t3/3−3t2+8t+4(m). Consider the motion of the particle from t=0 to t=5 sec. S1 is the total distance travelled and S2 is the distance travelled during retardation. if s1/s2=(3α+2)11 the find α.
x=t3/3−3t2+8t+4
v=t2−6t+8=(t−2)(t−4)
a=2(t−3)
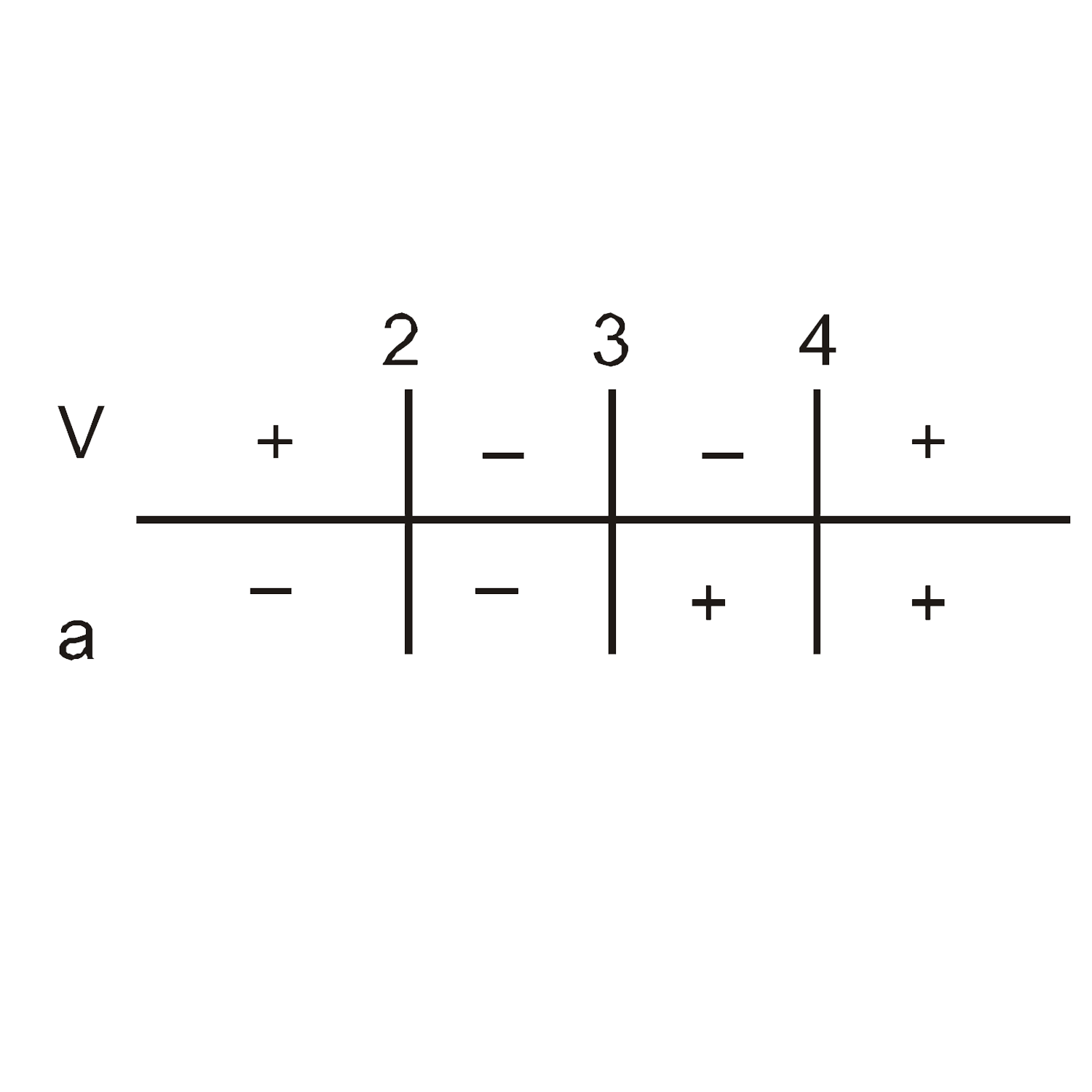
S1=(323×4)+(323−283)+(323−283)=203+83=283m.
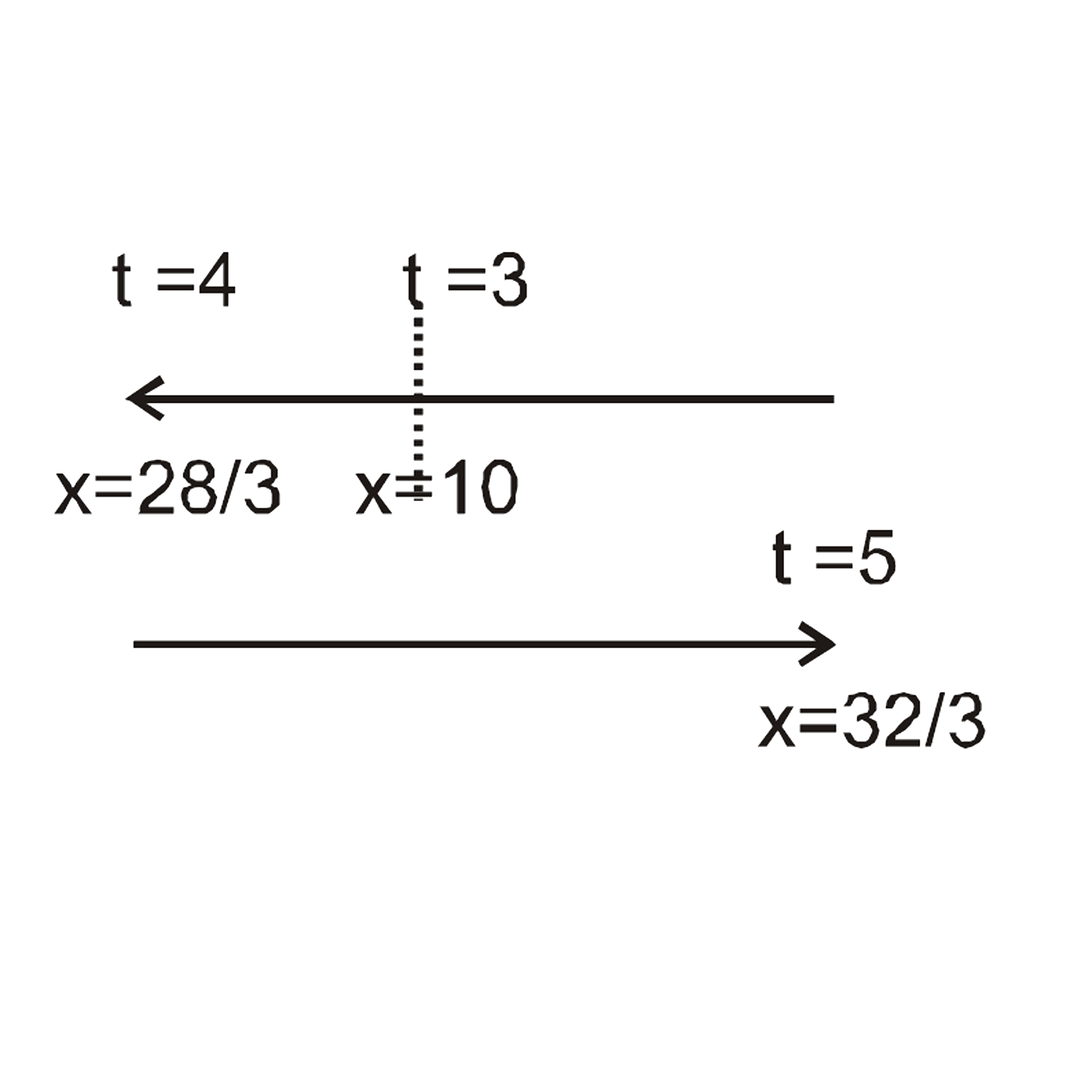
S2=(323−4)+(10−283)=203+23=223m
S1S2=2822=1411=3α+211⇒α=4
Topper's Solved these Questions
Similar Questions
Displacement of a particle of mass 2 kg varies with time as s=(2t2−2t+10)m. Find total work done on the particle in a time interval from t=0 to t=2s.
View SolutionThe position of a particle moving along a straight line is defined by the relation, x=t3−6t2−15t+40 where x is in meters and t in seconds.The distance travelled by the particle from t=0 to t=2 s is?
View Solution
Knowledge Check
- Question 1 - Select One
The distance s travelled by a particle moving on a straight line in time t sec is given by s=2t3−9t2+12t+6 then the initial velocity of the particle is
A6B−9C12D11 - Question 2 - Select One
A particle moves along a straight line such that its displacement at any time t is given by s=3t3+7t2+14t+5. The acceleration of the particle at t=1s is
A18m/s2B32m/s2C29m/s2D24m/s2 - Question 3 - Select One
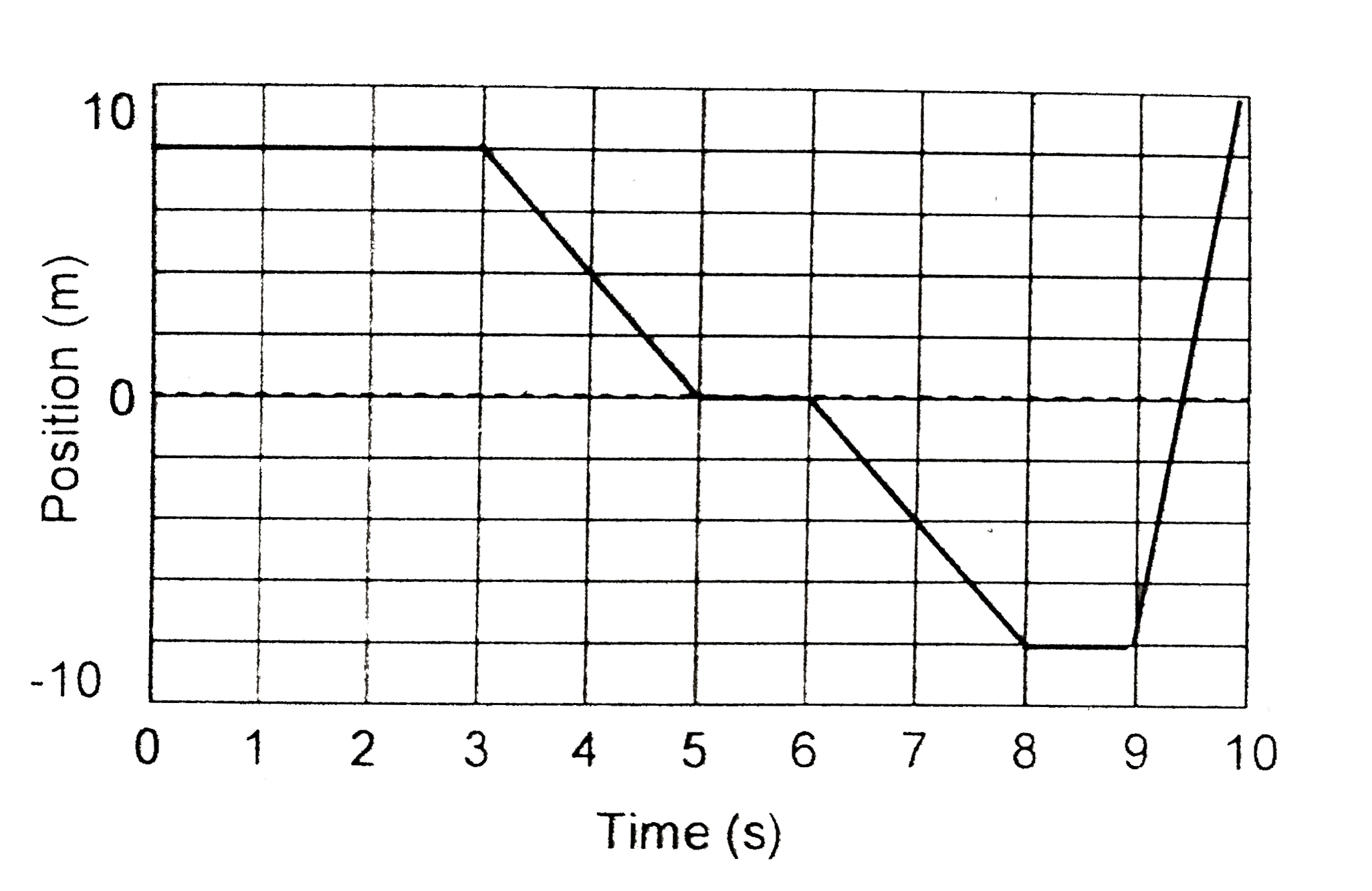
The position versus time graph of a particle moving along a straight line is shown. What is the total distance travelled by the particle from t=0s to t=10s?A2mB18 mC26mD34m
The position of a particle moving along x-axis varies eith time t as x=4t−t2+1. Find the time interval(s) during which the particle is moving along positive x-direction.
View SolutionVelocity (in m/s) of a particle moving along x-axis varies with time as, v=(10+5t−t2) At time t=0,x=0. Find
(a) acceleration of particle at t=2s and
(b) x-coordinate of particle at t=3sView Solution[" If position of particle moving in straight line is "],[" given by "x=(t^(3)-2t+10)m" ,where t is time in "],[" second,then acceleration of particle at "t=1],[" sec is "......]
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The distance travelled by particle from t=0 to t=2seconds is :View SolutionIf displacement of particle is s=t33−t22−t2+6, then velocity of the particle at t=4 sec. is
View Solution

