A cubical block of wood 10cm on a side floats at the interface between oil and water, as in fig. with its lower face 2cm below the interface. The intensity of the oli is 0.6gcm−3. The mass of the block is 1kg

340g
680g
80g
10g
The correct Answer is:B
mg=[100×2×1+100×8×0.6]g
∴M=(200+480)g=680g
Topper's Solved these Questions
Similar Questions
A cubical block of wood 10cm along each side floats at the interface between an oil and water with its lowest surface 2cm below the interface. If the height of oil and water columns are 10cm each and ρoil=0.8gcc, find a the mass of the block, b. the liquid pressure at the lower surface of the block.
View SolutionA cubical block of wood of edge 3 cm floats in water. The lower surface of the cube just touches the free end of a vertical spring fixed at the bottom of the pot. Find the maximum weight that can be put on the block without wetting it. Density of wood =800kgm−3 and spring constant of the spring =50Nm−1Takeg=10ms−2.
 ,
,
View Solution
Knowledge Check
A cubical block of wood 10 cm on a side floats at the interface between oil and water with its lower surface horizontal and 4 cm below the interface. The density of oil is 0.6gcm−3. The mass of block is
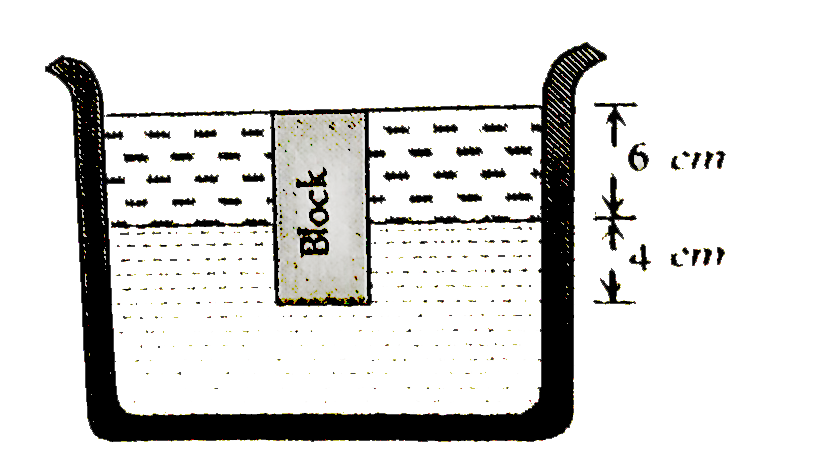 A706gB607gC760gD760g
A706gB607gC760gD760gA cubical block of wood 10cm on a side, floats at the interface of oil and water as shown in figure. The density of oil is 0.6gcm−3 and density of water is 1gcm−3. The mass of the block is
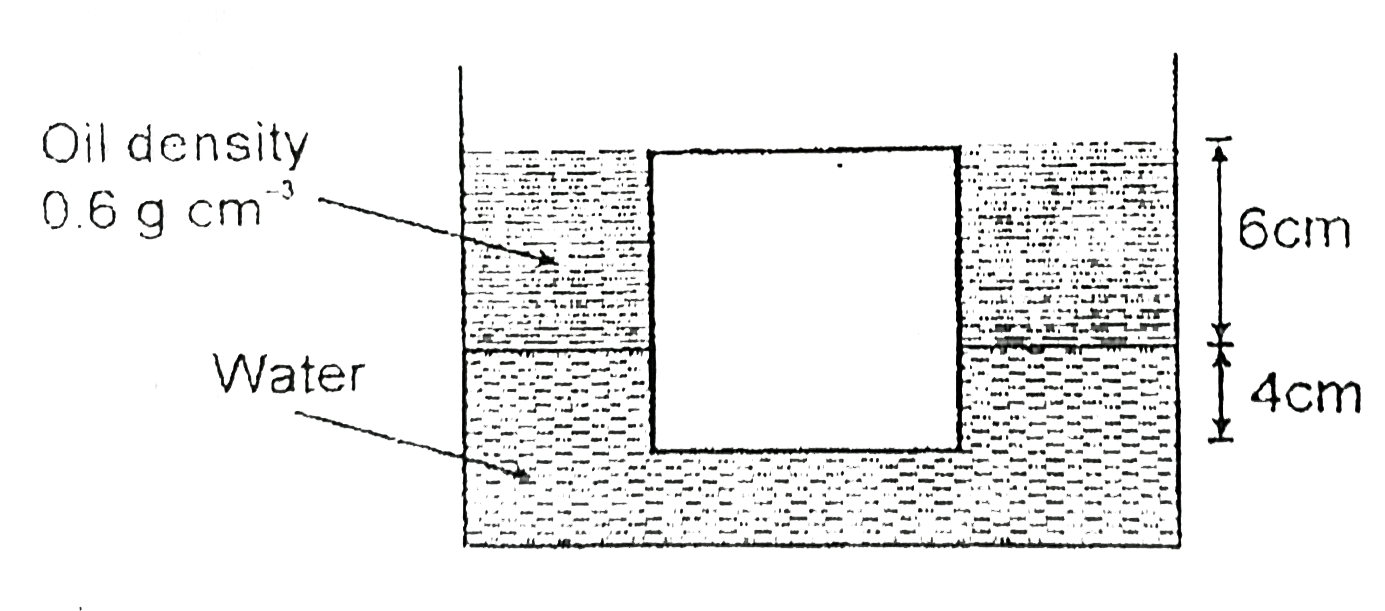 A706gB607gC760gD670g
A706gB607gC760gD670gA cubical block of side 10 cm floats at the interface of an oil and water. The pressure above that of atmosphere at the lower face of the block is
 A200Nm−2B680Nm−2C400Nm−2D800Nm−2
A200Nm−2B680Nm−2C400Nm−2D800Nm−2
A cubical block of iron 5 cm on each side is floating on mercury in a vessel. (i) what is the height of the block above mercury level ?
(ii) Water is poured in the vessel unitl it just covers the iron block. What is the height of water column . density of mercur 13.6gm/cm3. Density of iron 7.2 gm/cm3
View SolutionA cubical box of wood of side 30 cm weighting 21.6 kg floats on water with two faces horizontal. Calculate the depth of immersion of wood.
View SolutionThe density of ice is 0.921 g cm−3. Calculate the mass of a cubic block of ice which is 76 mm on each side.
View SolutionA cubical block of side 10cm floats at the interface of an oil and water as shown in the figure. The density of oil is 0.6gcm−3 and the lower face of ice cube is 2cm below the interface. The pressure above that of the atomosphere at the lower face of the block is

View SolutionA cubical block of wood of 10cm and mass 0.92kg floats on a tank of water with oil or rel. density 0.6. Thickness of oil is 4cm above water. When the block attains equilibrium with four of its sides edges verical:
View Solution

