A cubical block of wood 10cm along each side floats at the interface between an oil and water with its lowest surface 2cm below the interface. If the height of oil and water columns are 10cm each and ρoil=0.8gcc, find a the mass of the block, b. the liquid pressure at the lower surface of the block.
a. For the floating cube.

Weight of the cube=Buoyant force
⇒mg=Boil+Bwater
=8×102×ρoilg+2×102ρw×g
⇒m=800×0.8+200×1
=640+200=840g
b. The pressure at the lower surface of the cube is
poil+Pw=10100×(1+103)9.8
=980N/m2
= (Here we have used hoil=10cm and h2=2 cm above the lower surface).
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Solved Examples
Explore 7 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Exercise 4.1
Explore 11 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
A cubical block of wood weighing 200g has a lead piece fastened underneath. Find the mass of the lead pieces which will just allow the block to float in water. Specific gravity of wood is 0.8 and that of lead is 11.3.
(b) Solve the previous problem if the lead piece is fastened on the top surface of the block and the block is to float with its upper surface just dipping into water.
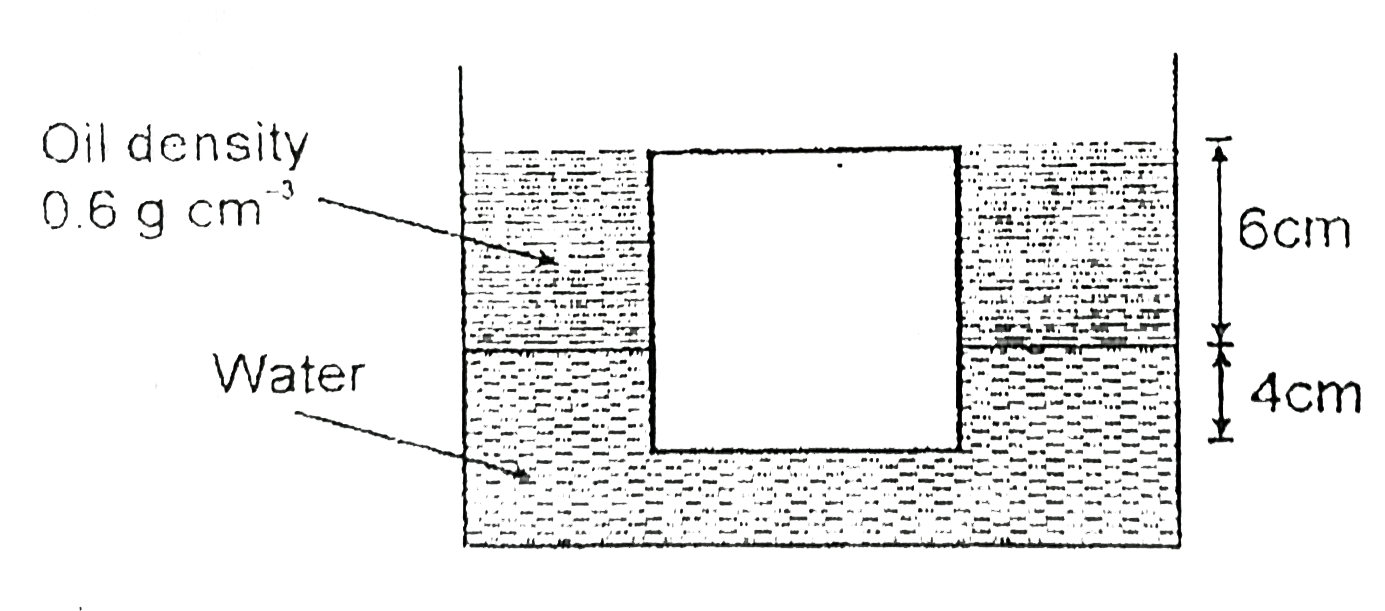
View SolutionA cubical block of wood 10cm on a side, floats at the interface of oil and water as shown in figure. The density of oil is 0.6gcm−3 and density of water is 1gcm−3. The mass of the block is
View Solution
Knowledge Check
A cubical block of wood 10 cm on a side floats at the interface between oil and water with its lower surface horizontal and 4 cm below the interface. The density of oil is 0.6gcm−3. The mass of block is
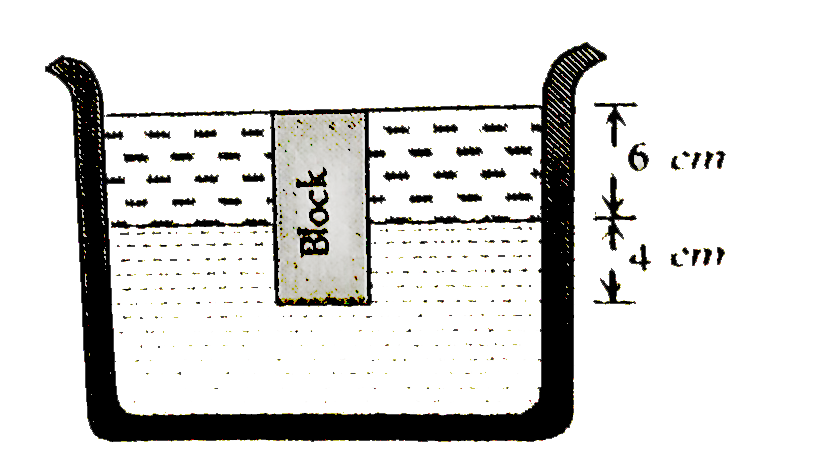 A706gB607gC760gD760g
A706gB607gC760gD760gA cubical block of wood 10cm on a side floats at the interface between oil and water, as in fig. with its lower face 2cm below the interface. The intensity of the oli is 0.6gcm−3. The mass of the block is 1kg
 A340gB680gC80gD10g
A340gB680gC80gD10gA cubical block of side 10 cm floats at the interface of an oil and water. The pressure above that of atmosphere at the lower face of the block is
 A200Nm−2B680Nm−2C400Nm−2D800Nm−2
A200Nm−2B680Nm−2C400Nm−2D800Nm−2
A cubical block of side 10cm floats at the interface of an oil and water as shown in the figure. The density of oil is 0.6gcm−3 and the lower face of ice cube is 2cm below the interface. The pressure above that of the atomosphere at the lower face of the block is

View SolutionA block of wood floats in water with (45)th of its volume submerged. In an oil, it floats with (910)th volume submerged. The ratio of the density of oil and water is
View SolutionA cubical block of wood having an edge 10 cm and mass 0.92 kg floats on a tank of water with oil of relative density 0.5 to a height of 4 cm above water. When the block attains equilibrium with four of its edges vertical
View SolutionA cubical block of copper of side 10cm is floating in a vessel containing mercury. Water is poured into the vessel so that the copper block just gets submerged. The height of water column is
(ρHg=13.6g/cc,ρCu=7.3g/cc,ρwater=1gm/cc)
View SolutionA cubical block of wood of 10cm and mass 0.92kg floats on a tank of water with oil or rel. density 0.6. Thickness of oil is 4cm above water. When the block attains equilibrium with four of its sides edges verical:
View Solution

