A cubical block of wood weighing has a lead piece fastened underneath. Find the mass of the lead pieces which will just allow the block to float in water. Specific gravity of wood is and that of lead is .
(b) Solve the previous problem if the lead piece is fastened on the top surface of the block and the block is to float with its upper surface just dipping into water.
(b)
.
(a) 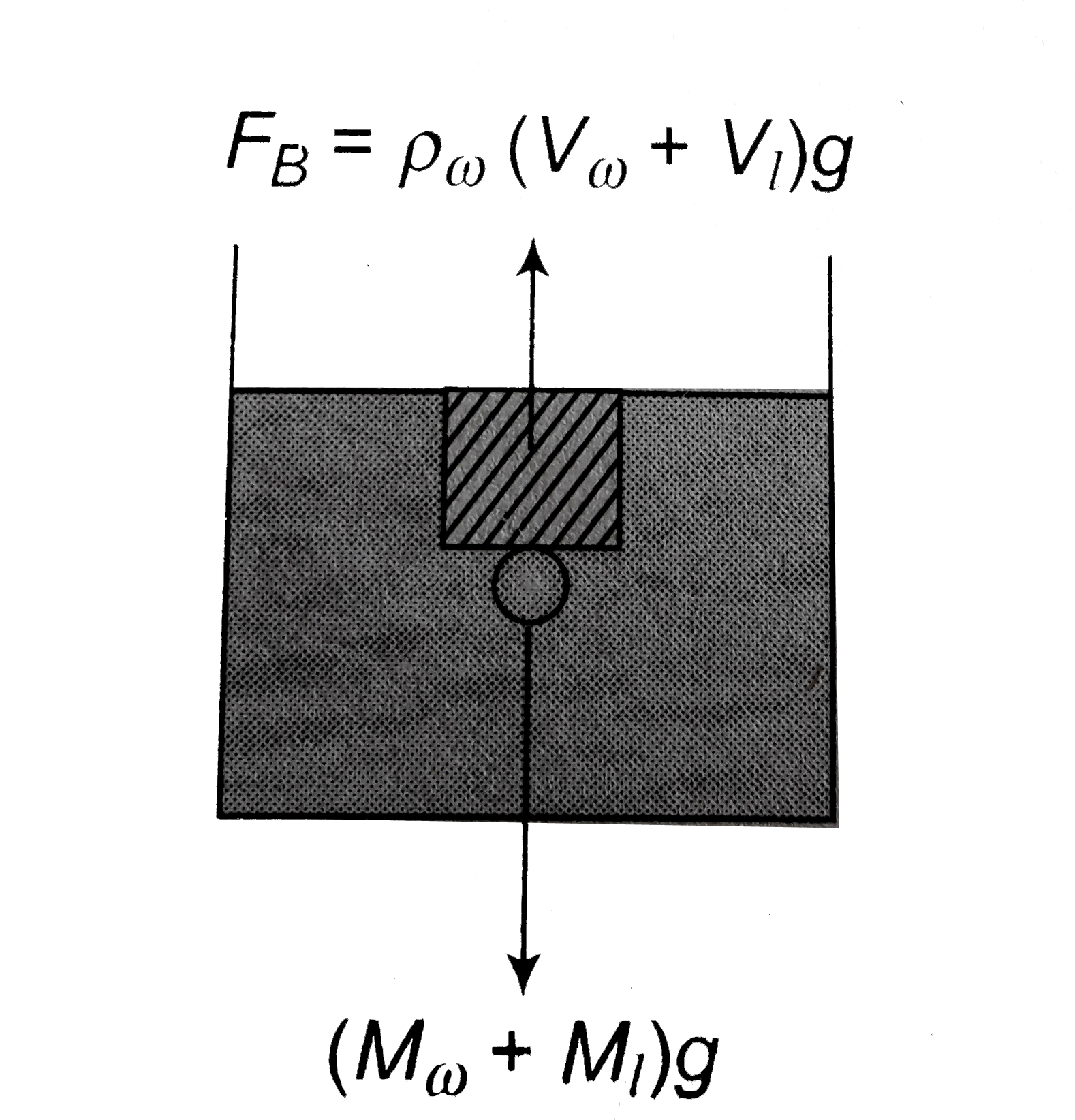
(b)  .
.
Topper's Solved these Questions
Similar Questions
Solve the prievious problem if the lead piece is fastened on the top surface of the block and the block is to float with its upper surface just dipping into water.
View SolutionA cubical block of wood weighing 200 g has a lead piece fastened underneath. Find the mass of the lead piece which will just alow the block of float in water. Specific gravity of wood is 0.8 and that of lead is 11.3.
View Solution
Knowledge Check
A cubical block of side 10 cm floats at the interface of an oil and water. The pressure above that of atmosphere at the lower face of the block is
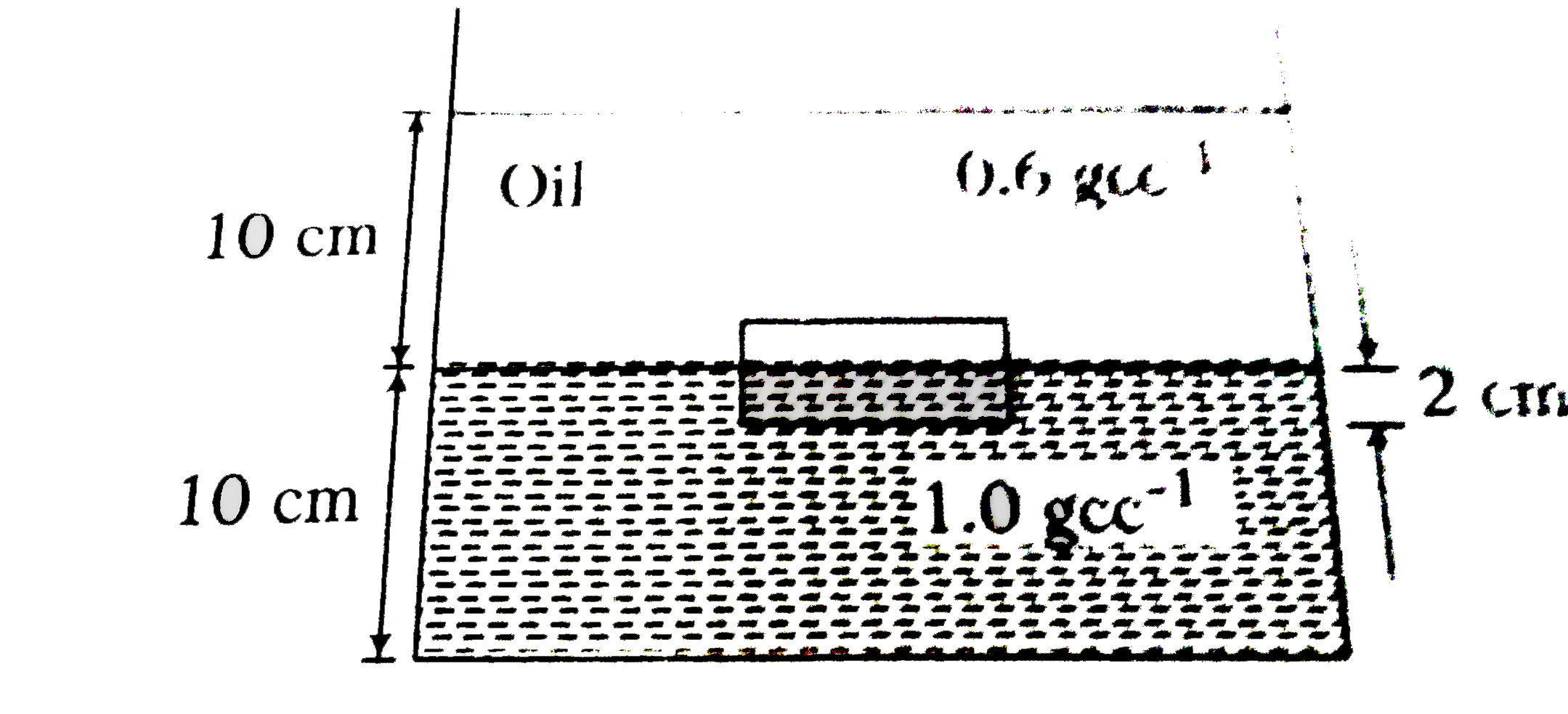 A200Nm−2B680Nm−2C400Nm−2D800Nm−2
A200Nm−2B680Nm−2C400Nm−2D800Nm−2A cubical block of wood 10cm on a side floats at the interface between oil and water, as in fig. with its lower face 2cm below the interface. The intensity of the oli is 0.6gcm−3. The mass of the block is 1kg
 A340gB680gC80gD10g
A340gB680gC80gD10gA block B of specific gravity 2 and another block C of specific gravity 0.5 .Both are joined together and they are floating water such that they are completely dipped inside water , the ratio of the masses of the blocks B and C is
A2:1B3:2C5:3D2:3
A cubical block of ice floating in water has to suport metal piece weighing 0.5 kg. What can be the minimum edge of the block so that it does not sink in water/ specific gravity of ice=0.9.
View SolutionA block of wood weight 4kg and has a relative density of 0.6 it is to be loaded with lead so that it will float in eater with 0.9 of its volume immersed. What weight of lead will be needed (a) if the is on top of the wood, (b) if the lead is attached below the wood ? (density of lead =11,340kgm−3)
View SolutionA piece of wood floats on water.
View SolutionWhy is the source of α-particles kept inside the lead block ?
View SolutionFind the density of a block of wood that floats in water with 0.1 of its volume above water
View Solution
