A 0.5kg block of brass (density 8×103Kgm−3) is suspended from a string. What is the tension in the string if the block is completely immersed in water? (g=10ms−2)
5N
0.58×103N
58N
[5−58]N
The correct Answer is:D
To find the tension in the string when the brass block is completely immersed in water, we will follow these steps:
Step 1: Calculate the true weight of the brass block.
The true weight (W) of the block can be calculated using the formula:
W=m⋅g
where:
- m=0.5kg (mass of the block)
- g=10m/s2 (acceleration due to gravity)
Substituting the values:
W=0.5kg⋅10m/s2=5N
Step 2: Calculate the volume of the brass block.
The volume (V) of the block can be calculated using the formula:
V=mρ
where:
- ρ=8×103kg/m3 (density of brass)
Substituting the values:
V=0.5kg8×103kg/m3=0.58000=6.25×10−5m3
Step 3: Calculate the weight of the water displaced.
The weight of the water displaced (W_displaced) can be calculated using the formula:
Wdisplaced=V⋅ρwater⋅g
where:
- ρwater=103kg/m3 (density of water)
Substituting the values:
Wdisplaced=6.25×10−5m3⋅103kg/m3⋅10m/s2
Wdisplaced=6.25×10−5⋅1000⋅10=0.625N
Step 4: Calculate the apparent weight of the block.
The apparent weight (W_apparent) of the block when submerged is given by:
Wapparent=W−Wdisplaced
Substituting the values:
Wapparent=5N−0.625N=4.375N
Step 5: Determine the tension in the string.
The tension (T) in the string is equal to the apparent weight of the block:
T=Wapparent=4.375N
Thus, the tension in the string when the block is completely immersed in water is 4.375 N.
---
The true weight (W) of the block can be calculated using the formula:
W=m⋅g
where:
- m=0.5kg (mass of the block)
- g=10m/s2 (acceleration due to gravity)
W=0.5kg⋅10m/s2=5N
The volume (V) of the block can be calculated using the formula:
V=mρ
where:
- ρ=8×103kg/m3 (density of brass)
V=0.5kg8×103kg/m3=0.58000=6.25×10−5m3
The weight of the water displaced (W_displaced) can be calculated using the formula:
Wdisplaced=V⋅ρwater⋅g
where:
- ρwater=103kg/m3 (density of water)
Wdisplaced=6.25×10−5m3⋅103kg/m3⋅10m/s2
Wdisplaced=6.25×10−5⋅1000⋅10=0.625N
The apparent weight (W_apparent) of the block when submerged is given by:
Wapparent=W−Wdisplaced
Substituting the values:
Wapparent=5N−0.625N=4.375N
The tension (T) in the string is equal to the apparent weight of the block:
T=Wapparent=4.375N
Topper's Solved these Questions
- FLUID MECHANICSBook:A2ZChapter:FLUID MECHANICSExercise:Continuity Equation And Bernoulli'S Theorem
Explore 32 Videos
- FLUID MECHANICSBook:A2ZChapter:FLUID MECHANICSExercise:Application Of Bernoulli'S Theorem And Velocity Of Efflux
Explore 19 Videos
- FLUID MECHANICSBook:A2ZChapter:FLUID MECHANICSExercise:Chapter Test
Explore 29 Videos
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBook:A2ZChapter:GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONExercise:Chapter Test
Explore 30 Videos
Similar Questions
A block of bras of mass 0.5 kg and density 8×103kg/m3 is suspended from a string. What will be the tension in the string if the block is completely immersed in water? (g=10ms−2)
View SolutionA block of mass 30 kg is suspended by three string as shown in fig, Find the tension in each string.
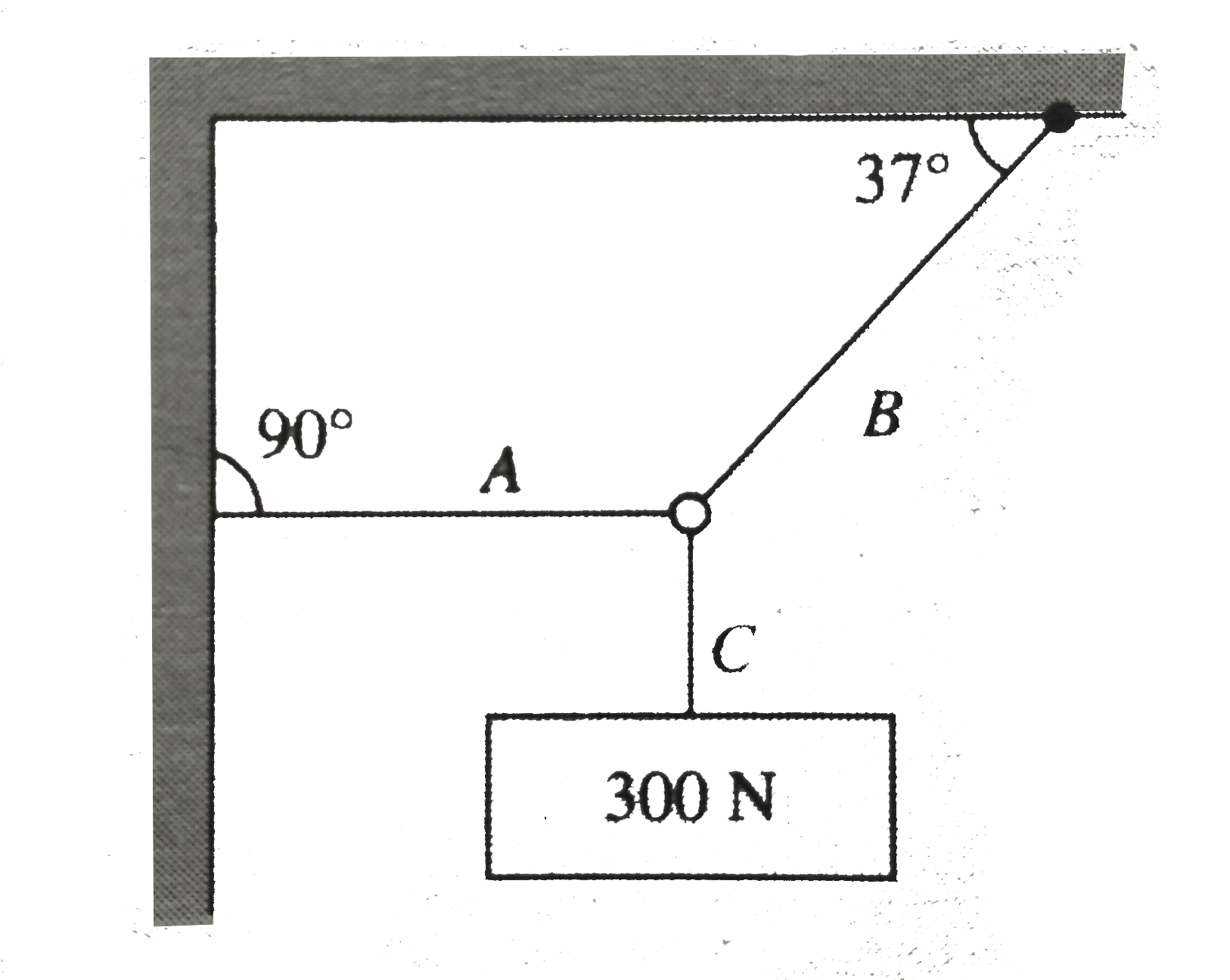
View Solution
Knowledge Check
A 100 kg block is suspended with the help of three strings A, B and C. The tension in the string A is
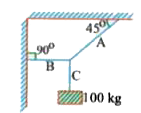 A50 g NB100 g NC20 g ND100√2gN
A50 g NB100 g NC20 g ND100√2gNA wooden block of mass 8 kg is tied to a string attached to the bottome of the tank. In the equilibrium the block is completely immersed in water. If relative density of wood is 0.8 and g=10ms−2, the tension T, in the string is
A120 NB100 NC80 ND20 NA wooden block of mass 8kg is tied to a string attached to the bottom of a tank. The block is completely inside the water. Relative density of wood is 0.8. Taking g=10m/s2, What is the tension in the string ?
A100NB80NC50ND20N
A 'block' of mass 10 kg is suspended with string as shown in figure. Find tension in the string. (g=10m/s2)
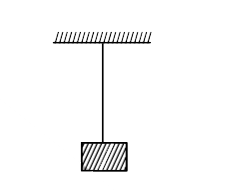
View SolutionA block of mass 10 kg is suspended with two strings as shown in the fig. Find the tensions T1andT2 in the two string.
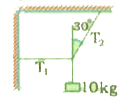
View SolutionA 10 kg steel ball is suspended by two strings as shown. The tensions in the two strings are: (g=9.8 m/s2)
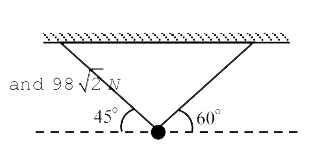
View SolutionA block of mass 10 kg is suspended by three strings as shown in figure . Tension T2 is

View SolutionA block of aluminium of mass 1 kg and volume 3.6×10−4m3 is suspended from a string and then completely immmersed in a container of water. The decreases in tension in the string after immersion is (use g=10ms−2)
View Solution

