Question

A tank with a square base of area ${\displaystyle 2m^2}$ is divided into two compartments by a vertical partition in the middle. There is a small hinged door of face area ${\displaystyle 20c{m}^2}$ at the bottom of the partition. Water is filled in one compartment and an acid of relative density 1.5 in the other, both to a height of 4m. The force necessary to keep the door closed is ${\displaystyle (Takeg=10m{s}^{-2})}$

Options

A. 10 N
B. 20 N
C. 40 N
D. 80 N

Answer

C

Explanation

(a) The situation is as shwon in the figure.

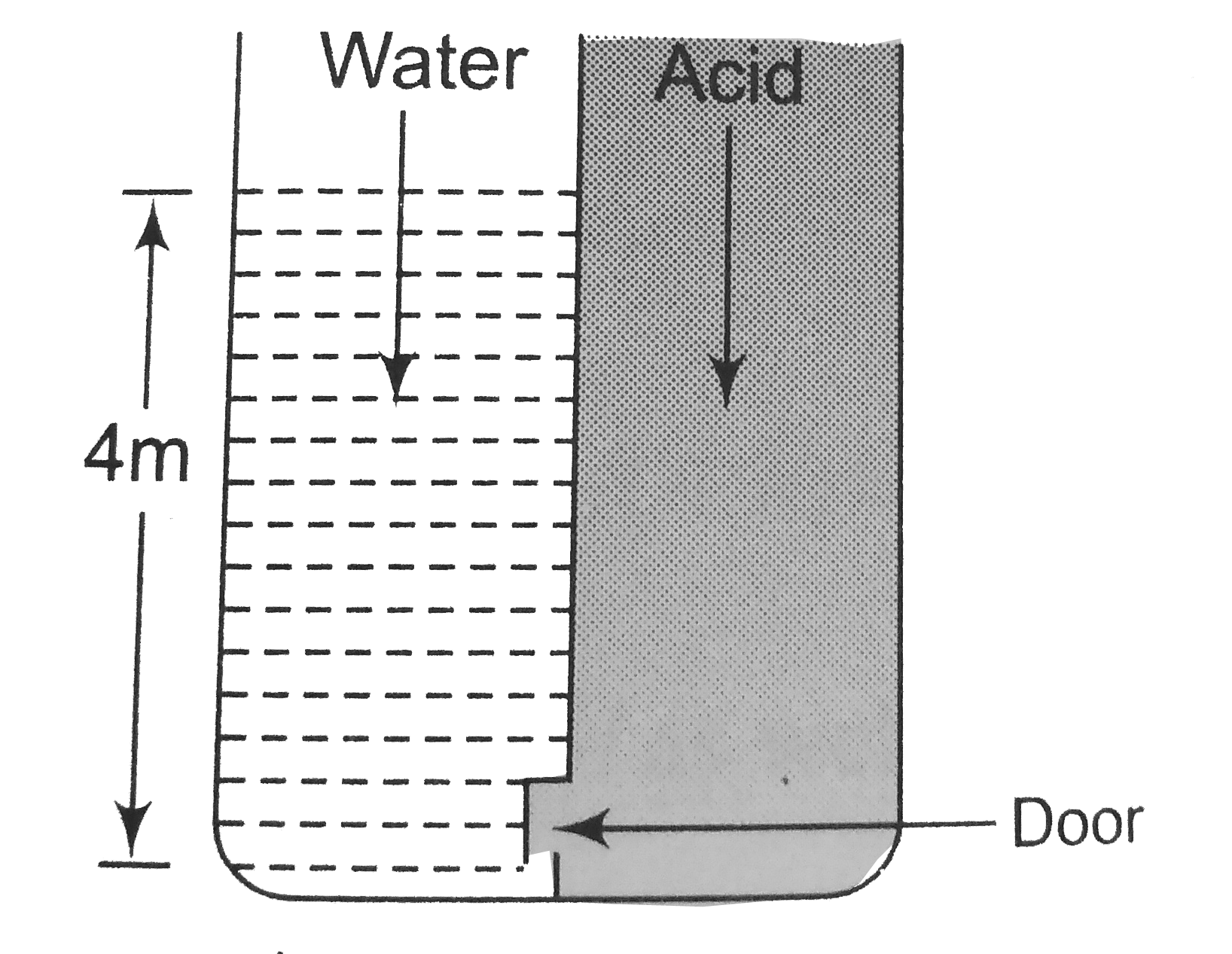
For compartment containing water,
` H = 4m, rho_w = 10^3 kg m^(-3)`
Pressure exerted by the water at the door at the bot- tom is
`P_w = rho hg = 10^3 kg m^(-3)xx 4m xx 10 ms^(-2)`
`=4 xx 10^4 N m^(-2)`
For compartment containing acid,
`rho a = 1.5 xx 10^3 kg m^(-3), h = 4m`
Pressure exerted by the acid at the door at the bottom is
`P_a = rho_a hg =1.5 xx 10^3 kg m^(-3) xx 4m xx 10ms ^(-3)`
`= 6xx 10^4 N m^(-2)`
Area of the door ` =20 cm^2 = 20 xx 10^(-4) m^2`
Force = Pressure xx Area = 40 N Thus, to keep the door closed the forece of 40 N must be applied horizontally from the water side.