Question

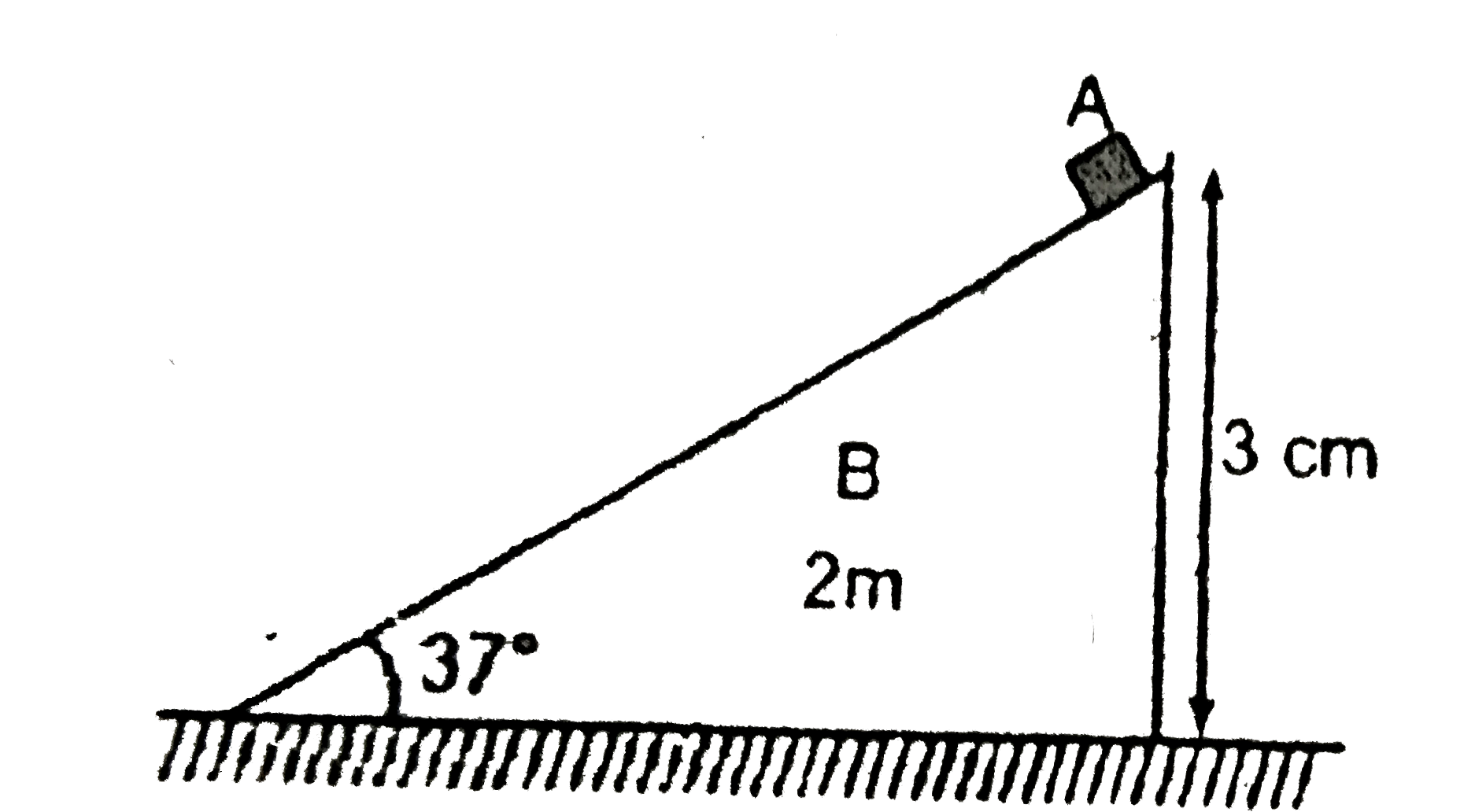
Figure, shows a vertical cross section of a surface. A and B are two points on the cross sections. A particle of mass 0.15kg is released from rest at A. (i) Assuming that particle reaches B with a speed of $8m/s$ and there is no resistance to motion, find the height of A above B.
(ii) Assuming instead that the particle reaches B with a speed of $6m/s$ and that the height of A above B is 4m, find work done against resistance to motion.

Explanation

(i) Here, `m=0.15 kg, v_(B)=8m//s`
If h is height of A above B, then accordint to the law of conservation of energy,
loss in PE (from A to B ) `=` gain in KE (at B)
`mgh=(1)/(2)mv^(2)`
`h=(v^(2))/(2g)=(8xx8)/(2xx9.8)=3.27m`
(ii) Now, `h^(')=4m,v_(B)=6m//s`
Accordint to the law of conservation of energy, Loss in PE (from A to B) `=` gain in KE at B + wokr down against friction
`mgh^(')=(1)/(2)mv_(B)^(2)+W`
`W=mgh^(')-(1)/(2)mv_(B)^(2)`
`=0.15xx9.8xx4-(1)/(2)xx0.15xx6^(2)`
`W=5.88-2.7`
`W=3.18J`