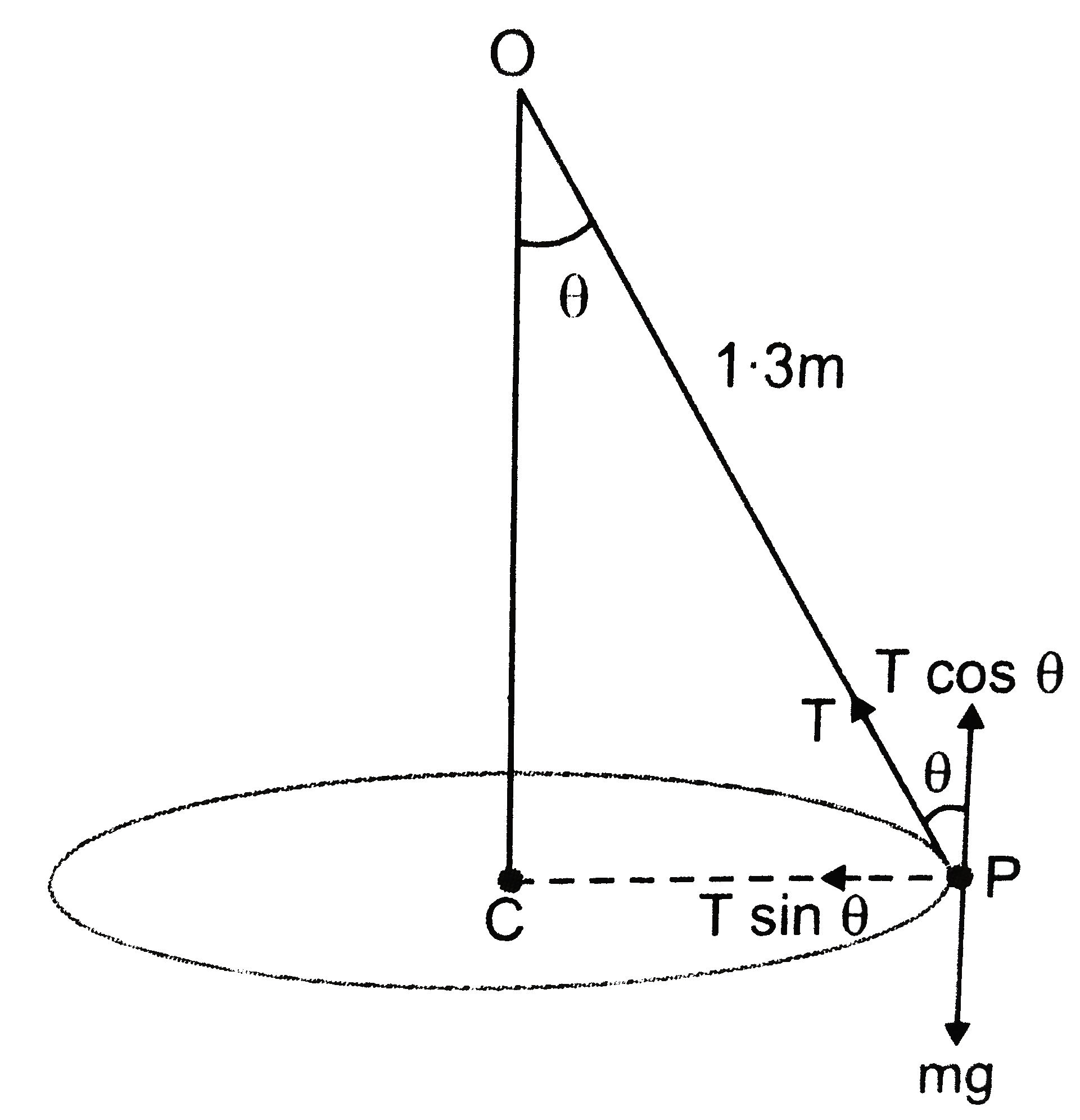
A sphere of mass $0.1 k g$ is attached to an inextensible string of length $1.3 m$ whose upper end is fixed to the ceilling The sphere is made to describe a horizontal circle of radius $0.5 m$ Calculate time period of revolution and tension in the string .

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $2.2 s; 1.06 N$ .

Updated on:21/07/2023

A particle of mass 200 g is attached to an ideal string of length 1.30 m whose upper end is fixed to ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is (g = 10 m/ $s^{2}$ )
A $\frac{13}{6} N$
B $\frac{11}{6} N$
C $\frac{26}{5} N$
DZero
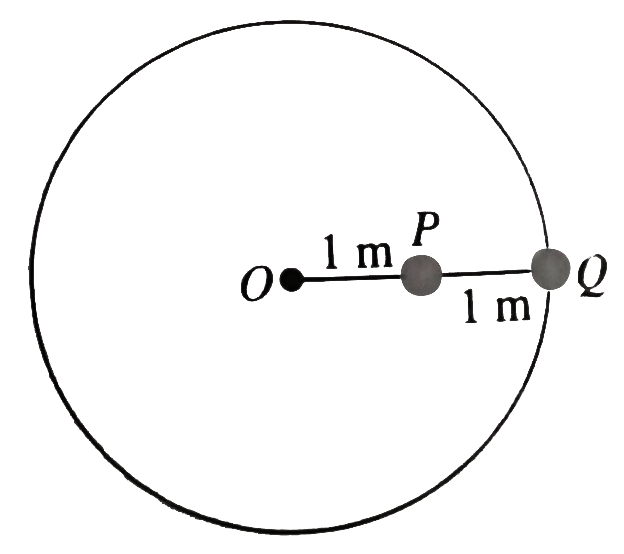
Two spheres of equal masses are attached to a string of length 2 m as shown in figure. The string and the spheres are then whirled in a horizontal circle about O at a constant rate. What is the value of the ratio:
A $\frac{1}{2}$
B $\frac{2}{3}$
C $\frac{3}{2}$
D2
A stone of mass $1 / 2$ kg is whriled round the end of a piece of string in a horizontal circle of radius half a meter with a uniform speed of $1 m / s$ . The tension in the string is
A $25 \times 10^{3}$ dynes
B $10^{5}$ dynes
C $5 \times 10^{4}$ dynes
D $4 \times 10^{5}$ dynes