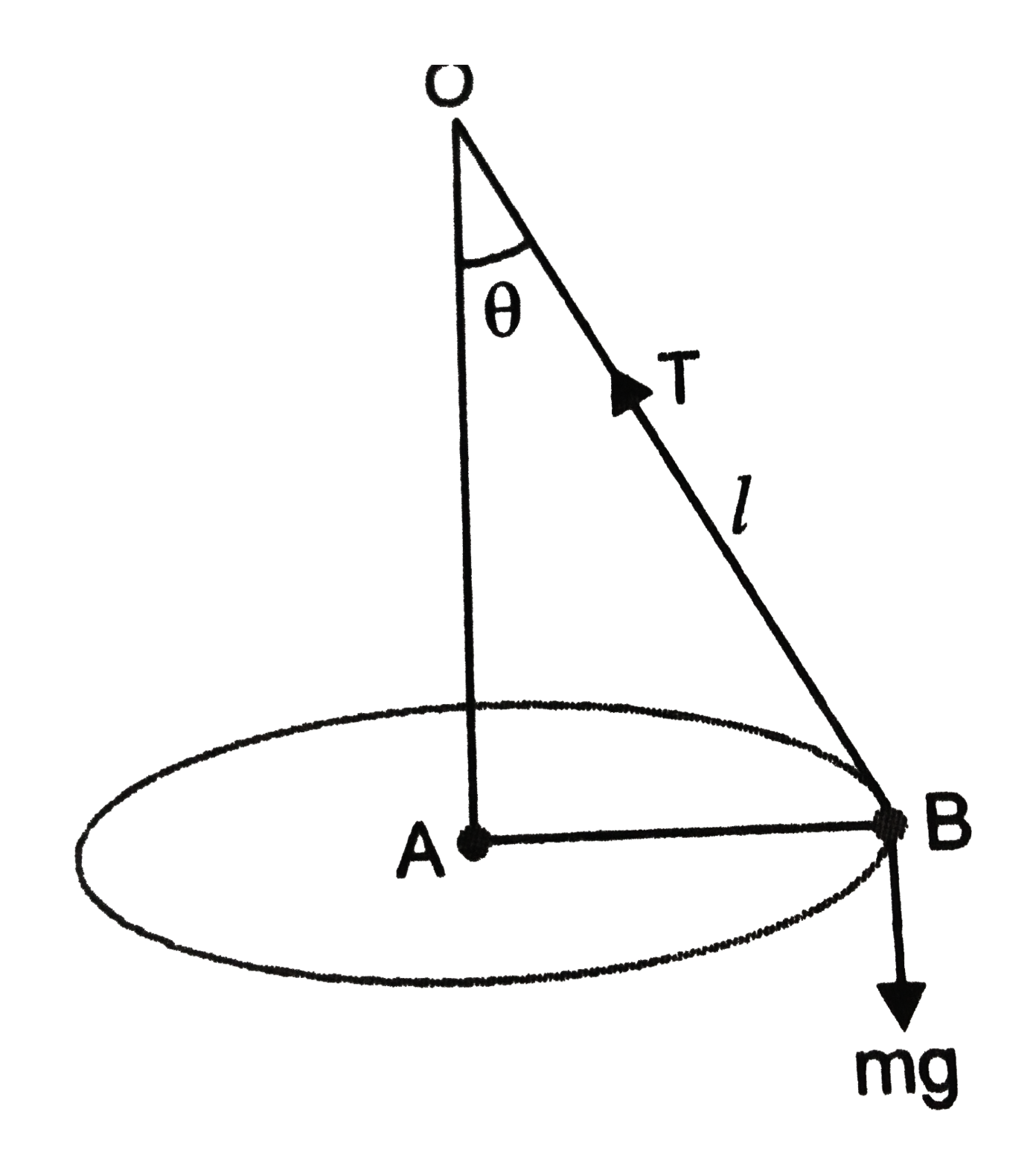
A sphere of mass 200 g is attached to an inextensible string of length 130 cm whose upper end is fixed to the ceilling . The sphere is made to describe a horizontal circle of radius 50 cm Calculate the periodic time of this conical pendulum and the tension in the string .
Here , m=200g,OB=l=130cm,
r=AB=50cm,t=?T=?
OA=√l2−r2=√(130)2−(50)2=120cm
As is clear from
Tcosθ=mg
Tsinθ=mυ2r=mrω2
Dividing , we get tanθ=mrω2mg=rω2g
ω=√gtanθr=2πr
t=2π√rgtanθ=2×227√0.59.8×5/12=2.19s
From (i) T=mgcosθ=2001000×9.812/13=2.12N
 .
.
Similar Questions
A sphere of mass0.1kg is attached to an inextensible string of length 1.3m whose upper end is fixed to the ceilling The sphere is made to describe a horizontal circle of radius 0.5m Calculate time period of revolution and tension in the string .
View SolutionA particle of mass 200g is attached to an ideal string of length 1.30 m whose upper end is fixed to ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is (g=10ms2)
View Solution
Knowledge Check
A particle of mass 200 g is attached to an ideal string of length 1.30 m whose upper end is fixed to ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is (g = 10 m/s2)
A136NB116NC265NDZero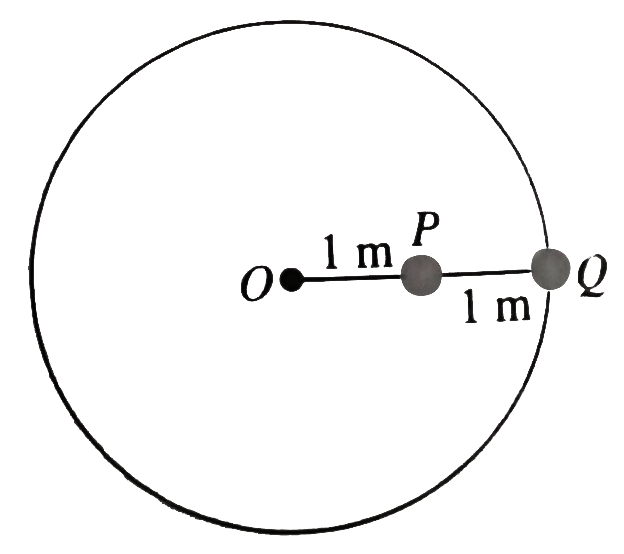
Two spheres of equal masses are attached to a string of length 2 m as shown in figure. The string and the spheres are then whirled in a horizontal circle about O at a constant rate. What is the value of the ratio:A12B23C32D2
A 100 g weight is tied at the end of a string and whirled around in horizontal circle of radius 15 cm at the rate of 3 revolutions per second. What is the tension in the string?
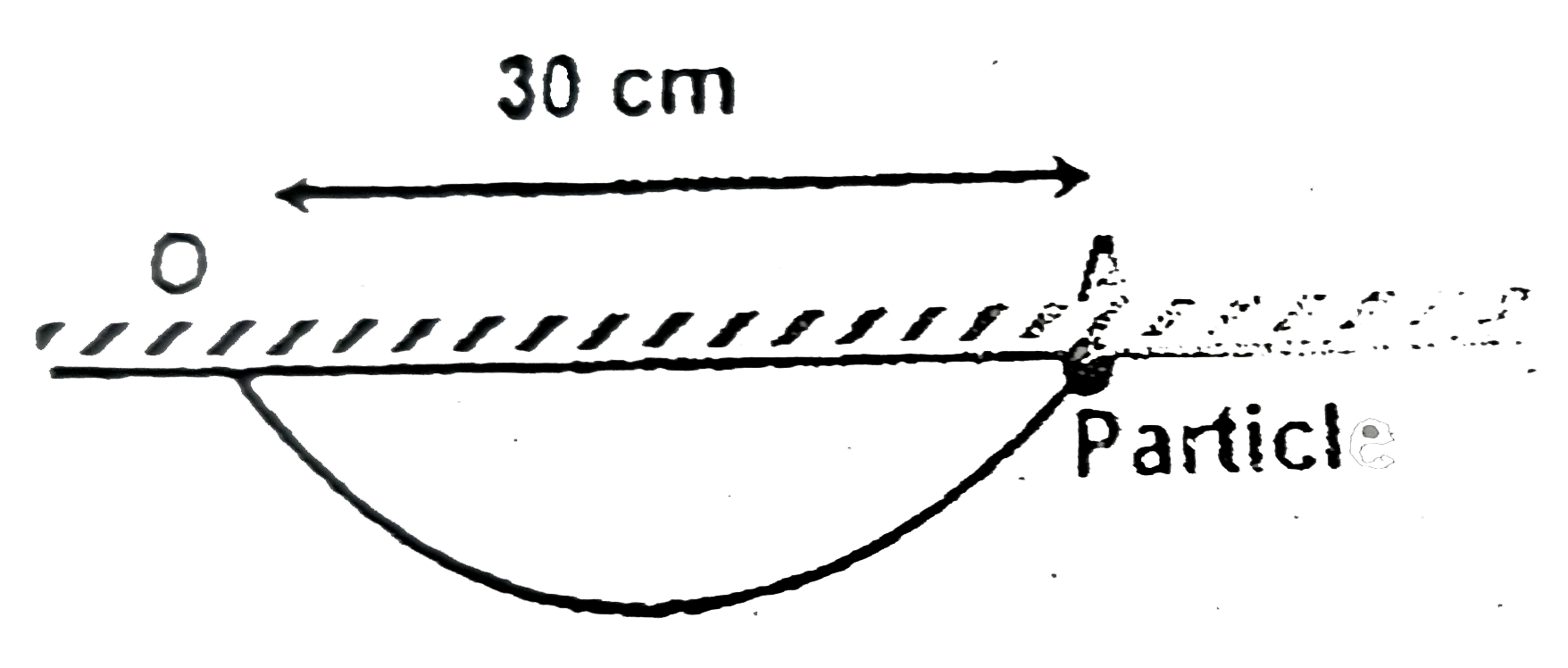
View SolutionA small ball of mass 100g is attached to a light and inextensible string of length 50cm. The string is tied to a support O and the mass m released from point A which is a' a horizontal distance of 30cm from the support. Calculate the speed of the ball is its lowest point of the trajectory.
View SolutionA particle of mass 21 g attached to a string of 70cm length Keeping the string always taut the ball describes a horizontal circle of radius 15cm Calculate the angular speed of the ball .
View SolutionA particle of mass 150 g is attached to one end of a massless inextensible string It is made to describe a vertical circle of radius 1 m When the string is making an angle of 48.2∘ with the vertical , its instantaneous speed is 2m/s What is the tension in the string in this position ? Whould this particle be able to complete its circular path ? .
View SolutionA ball of mass 0.1kg is suspended by a string 30cm long Keeping the string always taut the ball describe a horizontal circle of radius 15cm Calculate the angular speed of the ball .
View SolutionA particle of mass m is tied at the end of a light string of length L, whose other end is fixed at point C (fig), and is revolving in a horizontal circle of radius r to form a conical pendulum. A parallel horizontal beam of light forms shadow of the particle on a vertical wall.
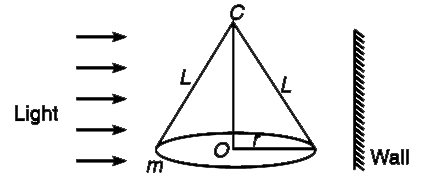
If the tension in the string is F find -
(a) The maximum acceleration of the shadow moving on the wall.
(b) The time period of the shadow moving on the wall.
View Solution
