Two waves are propagating to the point P along a straight line produced by two sources A and B of simple harmonic and of equal frequency. The amplitude of every wave at P is a and the phase of A is ahead by π/3 than that of B and the distance AP is greater than BP by 50cm. Then the resultant amplitude at the point P will be if the wavelength is 1 meter
2a
a√3
a√2
a
The correct Answer is:D
Path difference (Δx)=50cm=12m
Phase difference Δϕ=2πλ×Δx⇒ϕ=2π1×12=π
Total phase difference =π−π3=2π3
⇒A=√a2+a2+2a2cos(2π/3)=a
Topper's Solved these Questions
- WAVES AND ACOUSTICSBook:A2ZChapter:WAVES AND ACOUSTICSExercise:Beats
Explore 20 Videos
- WAVES AND ACOUSTICSBook:A2ZChapter:WAVES AND ACOUSTICSExercise:Stationary Waves
Explore 20 Videos
- WAVES AND ACOUSTICSBook:A2ZChapter:WAVES AND ACOUSTICSExercise:Equation And Energy Of Progressive Wave
Explore 16 Videos
- VECTORSBook:A2ZChapter:VECTORSExercise:Chapter Test
Explore 29 Videos
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Chapter Test
Explore 29 Videos
Similar Questions
Two light waves superimposing at the mid-point of the screen are coming from coherent sources of light with phase difference 3p rad. Their amplitudes are 1 cm each. The resultant amplitude at the given point will be.
View SolutionTwo waves are propagating with same amplitude and nearly same frequency in opposite direction, they result in
View Solution
Knowledge Check
Two waves are propagating to the point P along a straight line produced by two sources A and B of simple harmonic and of equal frequency. The amplitude of every wave at P is a and the phase of A is ahead by π/3 than that of B and the distance AP is greater than BP by 50cm. Then the resultant amplitude at the point P will be if the wavelength is 1 meter
A2aBa√3Ca√2DaThe resultant of two rectangular simple harmonic motion of the same frequency and unequal amplitude but differing in phase by π/2 is
ASimple harmonicBCircularCEllipticalDParabolicThe mass M shown in figure ocillates in simple harmonic motion with amplitude A.
The amplitude of the point P is
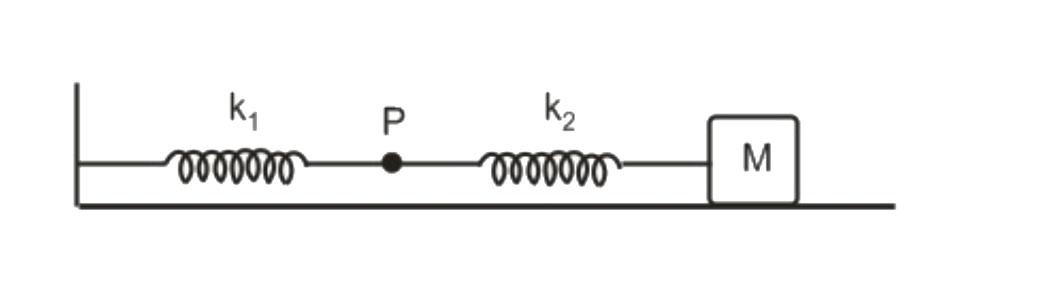 Ak1Ak2Bk2Ak2−k1Ck2Ak1+k2Dk2Ak1
Ak1Ak2Bk2Ak2−k1Ck2Ak1+k2Dk2Ak1
If two waves of amplitude a produce a resultant wave of amplitude a then the phase difference between the is
View SolutionTwo sine waves travel in the same direction in a medium. The amplitude of each wave is A and the phase difference between the two waves is 120^@. The resultant amplitude will be
View SolutionTwo sound waves travel in the same direction in a medium. The amplitude of each wave is A and the phase difference between the two waves is 120∘. The resultant amplitude will be
View SolutionTwo sources of sound A and B produce the wave of 350 Hz ,they vibrate in the same phase.The particle P is vibrating under the influence of these two wave.If the amplitudes at the point P Produced by the two waves is 0.3 mm and 0.4 mm ,then the resultant amplitude of the point P will be [Given AP -BP = 25 cm and the velocity of sound is 350 m/s ]
View SolutionTwo sources of sound A and B produces the wave of 350Hz. They vibrate in the same phase. The particle P is vibrating under the influence of these two waves, if the amplitudes at the point P produced by the two waves is 0.3mm and 0.4mm then the resultant amplitude of the point P will be when AP−BP=25cm and the velocity of sound is 350m/sec.
View Solution

