Two pulses travel in mutually opposite directions in a string with a speed of 2.5cm/s as shown in the figure. Initially the pulses are 10cm apart. What will be the state of the string after two seconds?
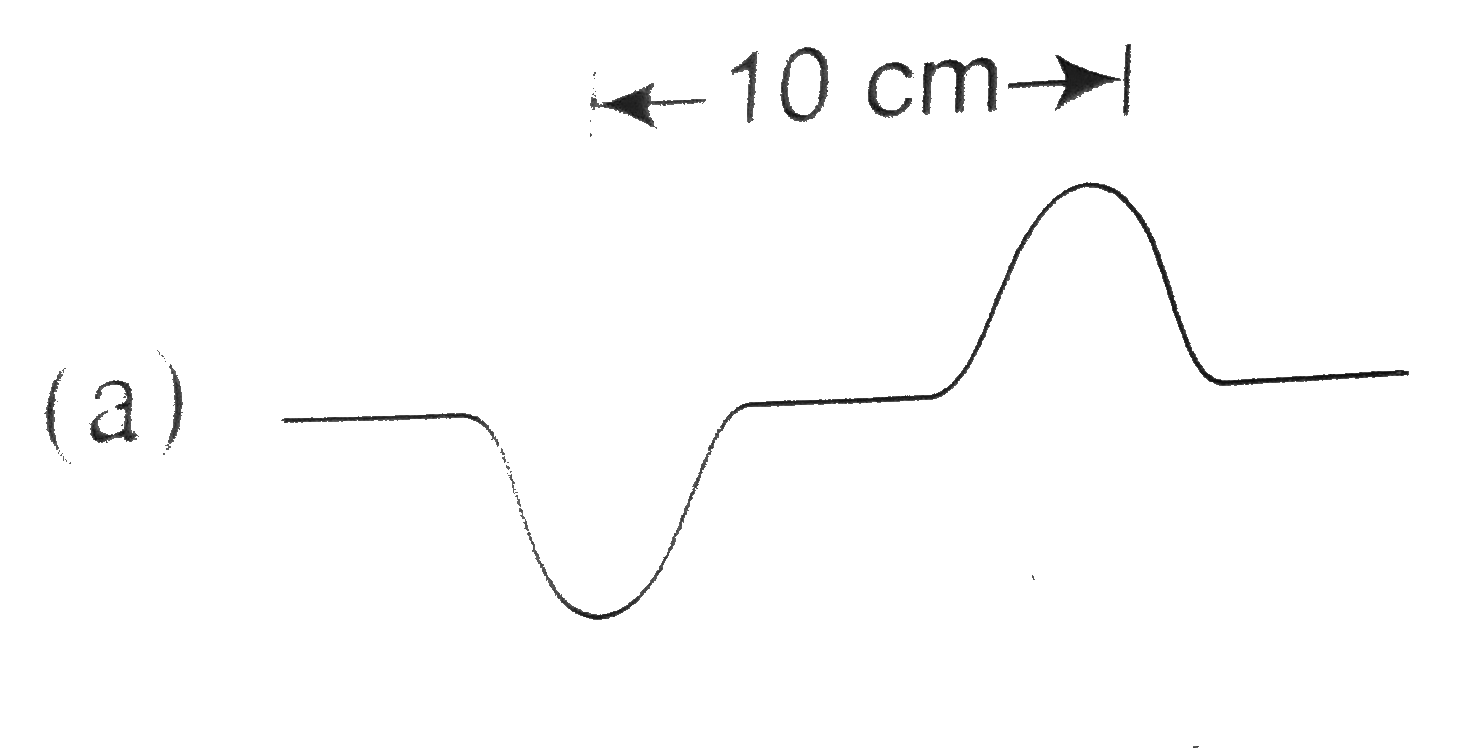
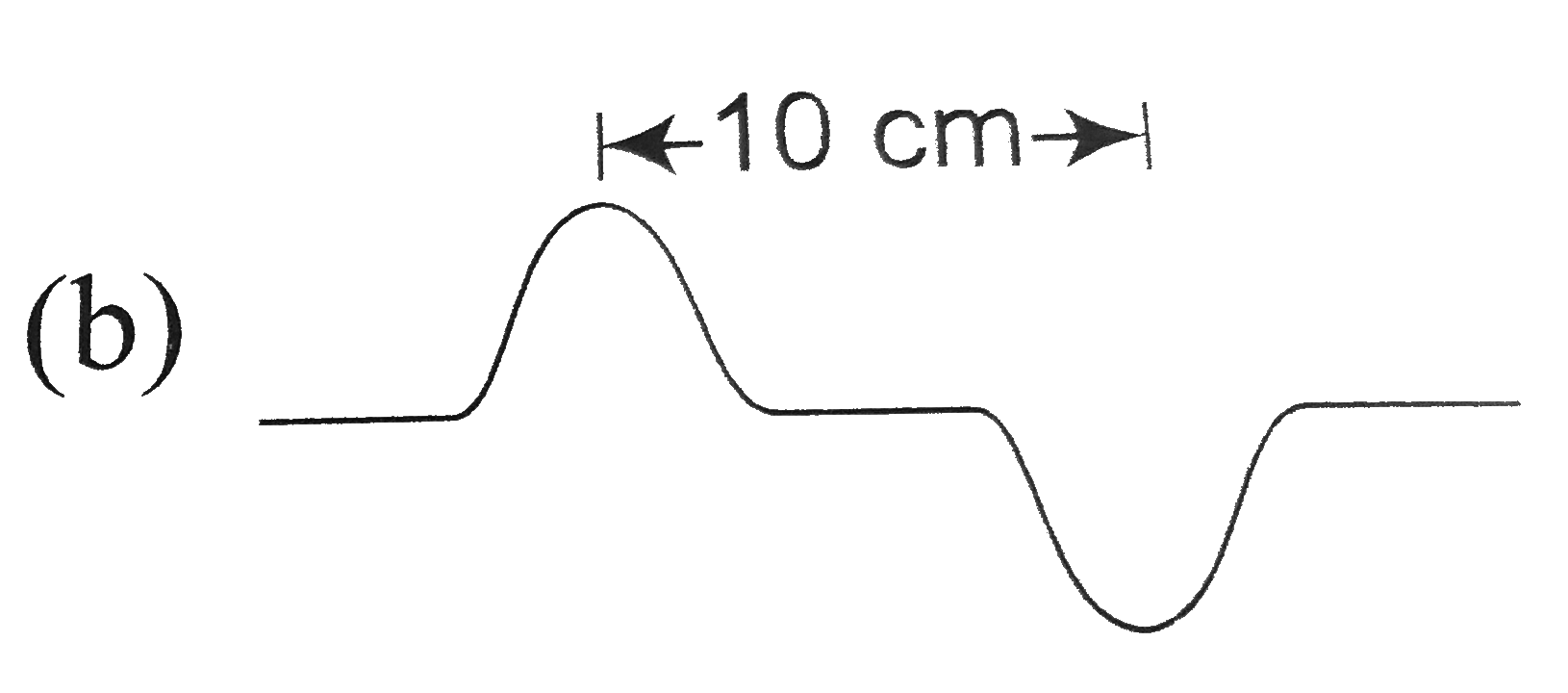

The correct Answer is:C
To solve the problem of determining the state of the string after two seconds, we can follow these steps:
Step 1: Understand the Initial Conditions
- The two pulses are initially 10 cm apart.
- Each pulse travels at a speed of 2.5 cm/s in opposite directions.
Step 2: Calculate the Distance Each Pulse Travels in 2 Seconds
- Since the speed of each pulse is 2.5 cm/s, we can calculate the distance traveled by each pulse in 2 seconds using the formula:
Distance=Speed×Time
- For 2 seconds:
Distance=2.5cm/s×2s=5cm
Step 3: Determine the New Positions of the Pulses
- Since the pulses are moving towards each other, we need to consider their new positions after 2 seconds.
- The first pulse moves 5 cm towards the second pulse, and the second pulse also moves 5 cm towards the first pulse.
Step 4: Calculate the New Distance Between the Pulses
- Initially, the distance between the two pulses was 10 cm.
- After 2 seconds, each pulse has moved 5 cm towards each other, so the new distance between the pulses is:
New Distance=Initial Distance−(Distance moved by Pulse 1+Distance moved by Pulse 2)
New Distance=10cm−(5cm+5cm)=0cm
Step 5: Conclusion
- After 2 seconds, the two pulses will meet at the same point on the string, resulting in a new state where the distance between them is 0 cm.
Summary of the Solution
- After 2 seconds, the two pulses will overlap completely at the same point on the string.
- The two pulses are initially 10 cm apart.
- Each pulse travels at a speed of 2.5 cm/s in opposite directions.
- Since the speed of each pulse is 2.5 cm/s, we can calculate the distance traveled by each pulse in 2 seconds using the formula:
Distance=Speed×Time
- For 2 seconds:
Distance=2.5cm/s×2s=5cm
- Since the pulses are moving towards each other, we need to consider their new positions after 2 seconds.
- The first pulse moves 5 cm towards the second pulse, and the second pulse also moves 5 cm towards the first pulse.
- Initially, the distance between the two pulses was 10 cm.
- After 2 seconds, each pulse has moved 5 cm towards each other, so the new distance between the pulses is:
New Distance=Initial Distance−(Distance moved by Pulse 1+Distance moved by Pulse 2)
New Distance=10cm−(5cm+5cm)=0cm
- After 2 seconds, the two pulses will meet at the same point on the string, resulting in a new state where the distance between them is 0 cm.
- After 2 seconds, the two pulses will overlap completely at the same point on the string.
Topper's Solved these Questions
- WAVES AND ACOUSTICSBook:A2ZChapter:WAVES AND ACOUSTICSExercise:Beats
Explore 20 Videos
- WAVES AND ACOUSTICSBook:A2ZChapter:WAVES AND ACOUSTICSExercise:Stationary Waves
Explore 20 Videos
- WAVES AND ACOUSTICSBook:A2ZChapter:WAVES AND ACOUSTICSExercise:Equation And Energy Of Progressive Wave
Explore 16 Videos
- VECTORSBook:A2ZChapter:VECTORSExercise:Chapter Test
Explore 29 Videos
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Chapter Test
Explore 29 Videos
Similar Questions
Two sinusoidal waves with identical wavelengths and amplitudes travel in opposite directions along a string with a speed of 15 cm/s. If the time interval between instants when the string is fiat is 0.20 s, what is the wavelength of the waves?
View SolutionTwo pulses travelling in opposite directions along a string are shown for t=0 in the figure. Plot the shape of the string at t= 1.0, 2.0, 3.0, 4.0 and 5.0s respectively .

View Solution
Knowledge Check

Two pulses are travelling along a string in opposite directions towards each other as shown in the figure. If the wave velocity is 2cm/s and the pulses are 6 cm apart, then after 1.5sec, the energy stored in the string will be (Assume shapes of pulses to be similar)Akinetic energy onlyBpotential energy onlyCkinetic energy as well as potential energyDnone of theseTwo wave pulses travel in opposite directions on a string and approch each other. The shape of the one pulse is same with respect to the other
Athe pulses will collide with each other and vanish after collisionBthe pulses will reflect from each other i.e., the pulse going towards right will finally move towards left and vice versa.Cthe pulse will pass through each other but their shapes will be modifiedDthe pulse will pass through each other without any change in their shapeTwo wave pulses travel in opposite directions on a string and approach each other. The shape of one pulse is inverted with respect to the other
AThe pulses will collide wilth each other and vanish after collisionBThe pulses will reflect from each other i.e., the poulse going towards right will finally move towards left and vice versaCThe pulses wil pass through each other but their shapes will be modifiedDthe pulses will pss through each other without any chasnge in their shapes.
Two triangular wave pulses are travelling toward each other on a stretched string as shown in Fig . 7.25. Both pulses are identical to each other and travels at 2.00cm/s. The leading edges of the pulses are 1.00cmapart at t=0 . Sketch the shape of the string at t=0.250s,t=0.500s,t=0.750s,t=1.000sandt=1.250s.
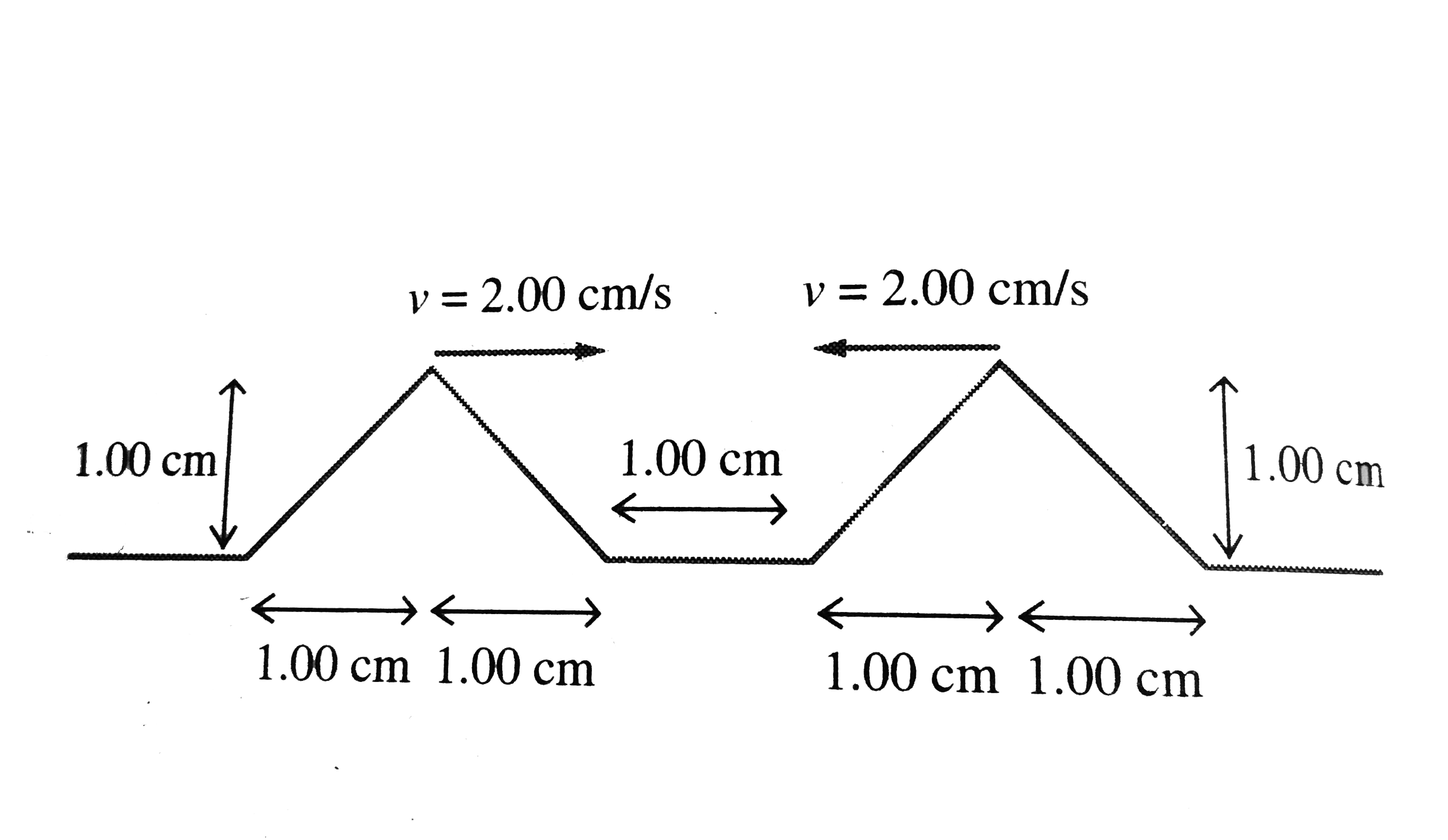
View SolutionTwo wave pulses travel in opposite directions on a string and approach each other. The shape of the one pulse in inverted with respect to the other.
View SolutionTwo identical harmonic pulses travelling in opposite directions in a taut string approach each other. At the instant when they completely overlap, the total energy of the string will be
 .
.
View SolutionA wave in a string has an amplitude of 2cm. The wave travels in the +ve direction of x axis with a speed of 128ms−1 and it is noted that 5 complete waves fit in 4m length of the string. The equation describing the wave is
View SolutionTwo sinusoidal waves with same wavelengths and amplitudes travel in opposite directions along a string with a speed 10ms−1. If the minimum time interval between two instant when the string is flat is 0.5s, the wavelength of the waves is
View Solution

