Two spring of spring constant k1 and k2 are joined in series The effective spring constant of the combination is given by
√k1k2
(k1+k2)/2
k1+k2
k1k2k1+k2
The correct Answer is:D
Let as consider two spring constants k1 and k2 joined in series as shown in the figure
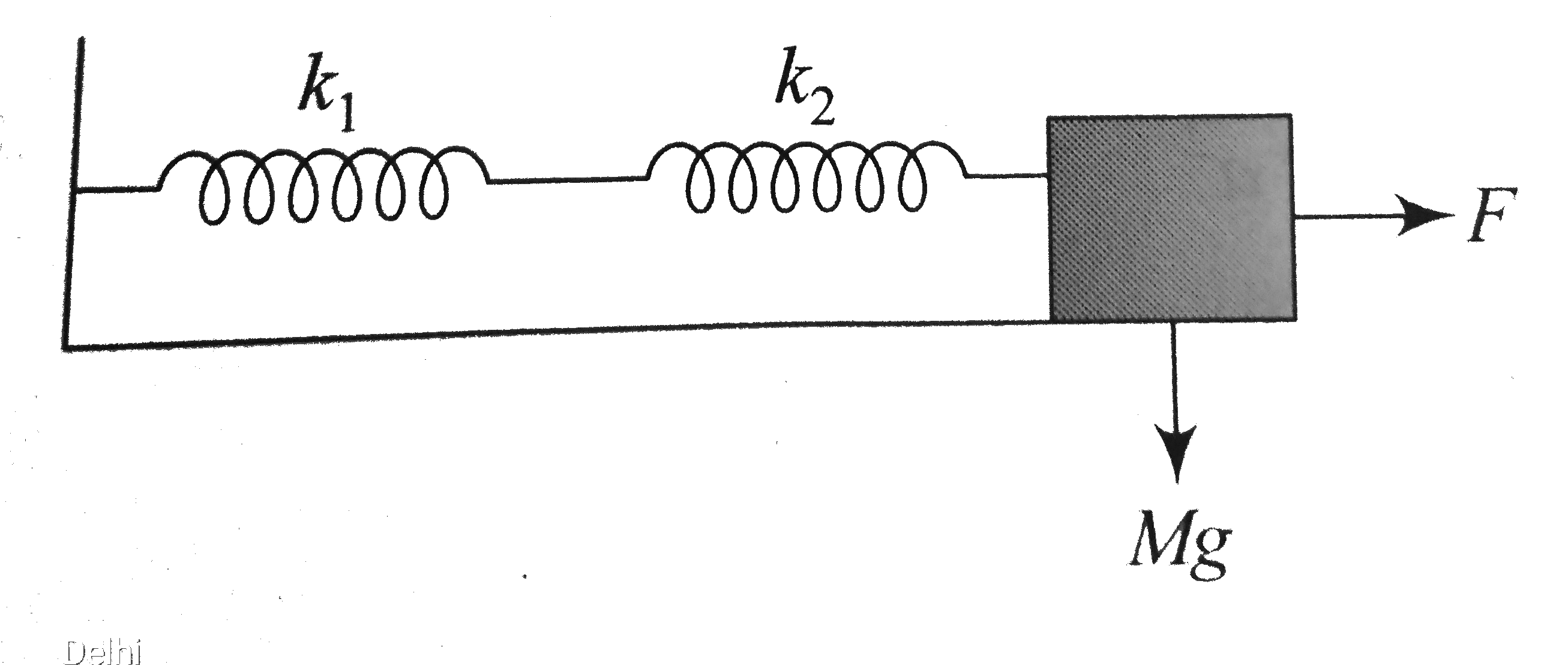
Under a force F they will strach by y1 and y2 so y=y1+y2
or Fk=F1k1=F2k2
but as spring and massless so force on then must be the same i.e. F1=F2=F
so 1k=1k1+1k2 or k=k1k2k1+k2
After in series conbination
1k2=1k1+1k2+k2+k1k1k2⇒k3=k1k2k1+(k2)⇒ks=k1k2k1+k2
Topper's Solved these Questions
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:AIIMS Questions
Explore 24 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Chapter Test
Explore 29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Assertion Reasoning
Explore 22 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Chapter Test
Explore 30 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Chapter Test
Explore 29 Videos
Similar Questions
Knowledge Check
Two springs of spring constantsK1 and K2 are joined in series. The effective spring constant of the combination is given by
A√k1k2B(k1+k2)2Ck1+k2Dk1k2(k1+k2)If two similar springs each of spring constant K1 are joined in series, the new spring constant and time period would be changed by a factor:
A12,√2B14,√2C14,2√2D12,√2A mass is suspended separately by two springs of spring constants k1 and k2 in successive order. The time periods of oscillations in the two cases are T1 and T2 respectively. If the same mass be suspended by connecting the two springs in parallel, (as shown in figure) then the time period of oscillations is T. The correct relations is
 AT2=T21+T22BT−2=T−21+T−22CT−1=T−11+T−12DT=T1+T2
AT2=T21+T22BT−2=T−21+T−22CT−1=T−11+T−12DT=T1+T2
A spring of spring constant k is cut in three equal pieces. The spring constant of each part will be
View SolutionTwo springs, of spring constants k1 and K2, have equal highest velocities, when executing SHM. Then, the ration of their amplitudes (given their masses are in the ratio 1:2) will be
View SolutionInfinite springs with force constantk , 2k, 4k and 8 k .... respectively are connected in series. The effective force constant of the spring will b
View SolutionA spring fo spring constant k is broken in the length ratio 1:3. The spring constant of larger part will be
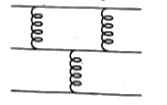
View SolutionEach of the above three springs are identical (they have the same equilibrium length and spring constant k). They are fixed together as shown in figure. What is the effective spring constant of the assembly?
View Solution



