A particle of mass m oscillates with simple harmonic motion between points x1 and x2 the equilibrium position being O its potential energy in plotted it will be as given bellow in the graph
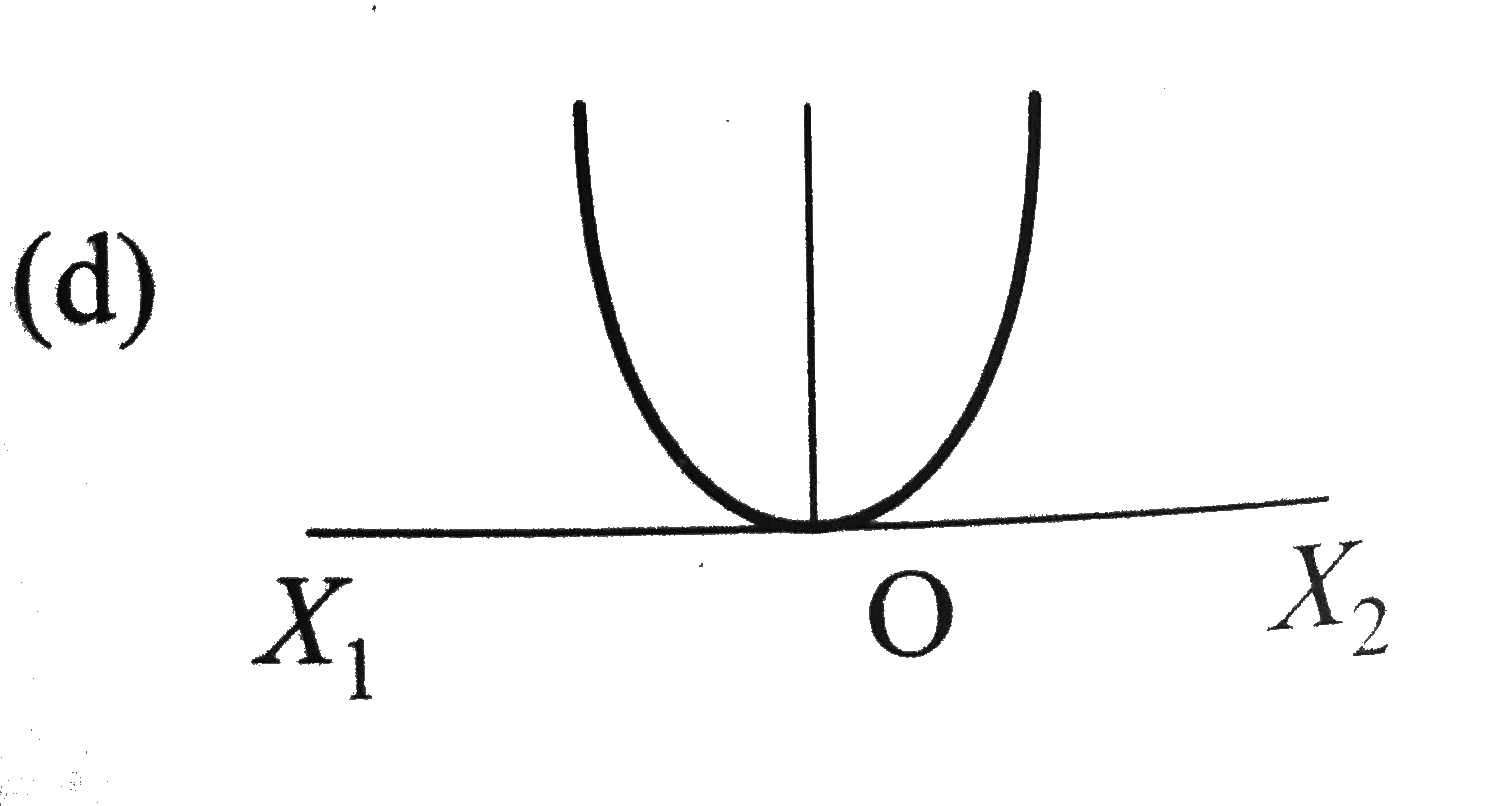
The correct Answer is:D
Potential energy of particle performing SHM is given by PE=12mω2y2 i.e. veries parabolicalty such thet at mean position is become zero maximum at exterme position
Topper's Solved these Questions
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:AIIMS Questions
Explore 24 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Chapter Test
Explore 29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Assertion Reasoning
Explore 22 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Chapter Test
Explore 30 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Chapter Test
Explore 29 Videos
Similar Questions
The potential energy of a particle, executing a simple harmonic motion, at a dis"tan"ce x from the equilibrium position is proportional to
View SolutionA particle executes simple harmonic motion of ampliltude A. At what distance from the mean position is its kinetic energy equal to its potential energy?
View Solution
Knowledge Check
A particle of mass m oscillates with simple harmonic motion between points x1 and x2, the equilibrium position being O. Its potential energy is plotted. It will be as given below in the graph
A B
B C
C D
D
A particle of mass m oscillates with simple harmonic motion between two points x1 and x2 the equilibrium position being O its potential energy is plotted on the graph which of the following curve represents the phenomenon?
A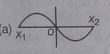 B
B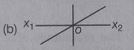 C
C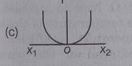 D
D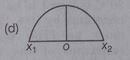
A particle of mass m oscillates with simple harmonic motion between two points x1 and x2 the equilibrium position being O its potential energy is plotted on the graph which of the following curve represents the phenomenon?
A B
B C
C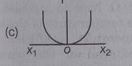 D
D
A particle oscillates simple harmonic motion with a period of 16s. Two second after crossing the equilibrium position its velocity becomes 1m/s. The amplitude is
View SolutionA particle is executing simple harmonic motion between exterme positions given by (−1,−2,−3)cm and (1,2,1)cm. Its amplitude of oscillation is
View SolutionA particle is vibrating in a simple harmonic motion with an amplitude of 4 cm . At what displacement from the equilibrium position, is its energy half potential and half kinetic
View SolutionA particle starts oscillating simple harmonically from its equilibrium position then, the ration of kinetic energy and potential energy of the particle at the time T/12 is: (T=time period)
View SolutionA body is executing a simple harmonic motion such that its potential energy is U1at U2aty When the displacement is x+y the potential energy will be
View Solution

