Two particle of same time period (T) and amplitude undergo SHM along the same line with initial and phase of π/6. If they start at the same point along the opposite directions. Find the time other which they will meet again for the first time
T/8
T/4
T/2
T
The correct Answer is:C
To solve the problem, we need to analyze the motion of the two particles undergoing Simple Harmonic Motion (SHM) with the same amplitude and time period but with a phase difference of π6.
1. Understanding the Motion:
- Both particles have the same amplitude A and time period T.
- The first particle starts at the maximum position A and moves in the positive direction.
- The second particle starts at the same point A but moves in the negative direction.
2. Equations of Motion:
- The displacement of the first particle can be expressed as:
x1(t)=Asin(ωt)
- The displacement of the second particle, which has a phase difference of π6, can be expressed as:
x2(t)=Asin(ωt+π6)
- Here, ω=2πT is the angular frequency.
3. Finding the Condition for Meeting:
- The particles will meet when their displacements are equal:
x1(t)=x2(t)
- This gives us:
Asin(ωt)=Asin(ωt+π6)
- Dividing both sides by A (assuming A≠0):
sin(ωt)=sin(ωt+π6)
4. Using the Sine Function Property:
- The sine function has the property that sin(x)=sin(y) implies:
x=y+2nπorx=π−y+2nπ
- Applying this to our equation:
- For the first case:
ωt=ωt+π6+2nπ⇒No solution
- For the second case:
ωt=π−(ωt+π6)+2nπ
Simplifying this gives:
2ωt=π−π6+2nπ
2ωt=5π6+2nπ
ωt=5π12+nπ
5. Finding the First Meeting Time:
- For n=0:
ωt=5π12
t=5π12ω
- Since ω=2πT:
t=5π12⋅2πT=5T24
Final Answer:
The two particles will meet again for the first time after a time of 5T24.
- Both particles have the same amplitude A and time period T.
- The first particle starts at the maximum position A and moves in the positive direction.
- The second particle starts at the same point A but moves in the negative direction.
- The displacement of the first particle can be expressed as:
x1(t)=Asin(ωt)
- The displacement of the second particle, which has a phase difference of π6, can be expressed as:
x2(t)=Asin(ωt+π6)
- Here, ω=2πT is the angular frequency.
- The particles will meet when their displacements are equal:
x1(t)=x2(t)
- This gives us:
Asin(ωt)=Asin(ωt+π6)
- Dividing both sides by A (assuming A≠0):
sin(ωt)=sin(ωt+π6)
- The sine function has the property that sin(x)=sin(y) implies:
x=y+2nπorx=π−y+2nπ
- Applying this to our equation:
- For the first case:
ωt=ωt+π6+2nπ⇒No solution
- For the second case:
ωt=π−(ωt+π6)+2nπ
Simplifying this gives:
2ωt=π−π6+2nπ
2ωt=5π6+2nπ
ωt=5π12+nπ
- For n=0:
ωt=5π12
t=5π12ω
- Since ω=2πT:
t=5π12⋅2πT=5T24
The two particles will meet again for the first time after a time of 5T24.
Topper's Solved these Questions
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
22 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - NEET Questions
39 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Superposition Of Shm And Compound Pendulum
19 Videos
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test
30 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test
29 Videos
Similar Questions
Two particles execute SHM of same time period but different amplitudes along the same line. One starts from mean position having amplitude A and other starts from extreme position having amplitude 2A. Find out the time when they both will meet?
View SolutionTwo particles have time periods T and 5T/4. They start SHM at the same time from the mean postion. After how many oscillations of the particle having smaller time period, they will be again in the same phase ?
View Solution
Knowledge Check
Time period (T) and amplitude (A) are same for two particle which undergoes SHM along the same line. At one particular instant one particle is at phase3π2and the other is at zero, while moving in the same direction. Find the time at which they will cross each other
A4T/2B3T/8C3T/4D3T/7Two particles execute SHM of the same time period along the same straight lines. They cross each other at the mean position while going in opposite directions. Their phase difference is
Aπ2BπC3π2D2πTwo particles undergo SHM along parallel lines with the same time period (T) and equal amplitudes. At particular instant, one particle is at its extreme position while the other is at its mean position. The move in the same direction. They will cross each other after a further time.
AT/2B3T/8CT/6D3T/4
Two particles start moving from same position on a circle of radius 20 cm with speed 40π m/s and 36π m/s respectively in the same direction. Find the time after which the particles will meet again.
View SolutionTwo particles P1 and P2 are performing SHM along the same line about the same meabn position , initial they are at their position exterm position. If the time period of each particle is 12 sec and the difference of their amplitude is 12cm then find the minimum time after which the seopration between the particle becomes 6cm
View SolutionTwo particles undergo SHM along the same line with the same time period (T) and equal amplitude (A). At a particular instant one is at x = -A and the other is at x = 0. If they start moving in the same direction then they will cross each other at
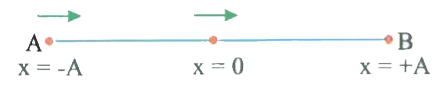
(i) t=4T3
(ii) t=3T8
(iii) x=A2
(iv) x=A√2
View SolutionTwo particles undergo SHM along the same line with the same time period (T) and equal amplitude (A). At a particular instant one is at x=−A and the other is at x=0. If they start moving in the same direction then they will cross each other at

(i) t=4T3 (ii) t=3T8 (iii) x=A2 (iv) x=A√2
View SolutionTwo particle undergoes SHM along parallel line with the same time period (T) and equal amplitude At a particular instant , one particle is at its extereme position while the other is at its mean position .They move in the same direction .They will cross each other after a further time
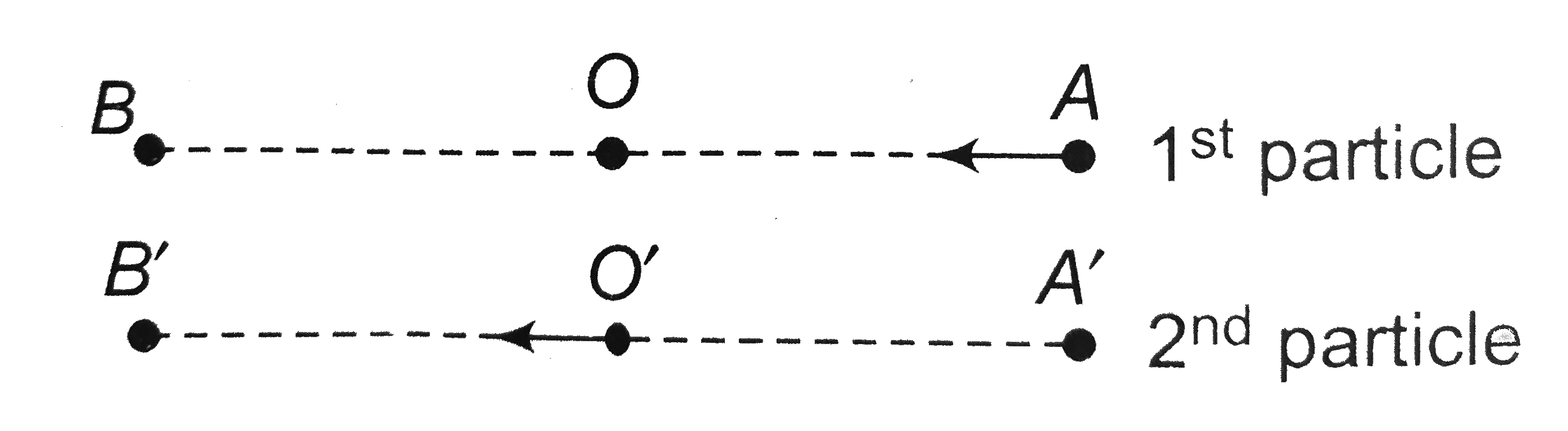
View Solution