Two particles execute SHM of same time period but different amplitudes along the same line. One starts from mean position having amplitude A and other starts from extreme position having amplitude 2A. Find out the time when they both will meet?
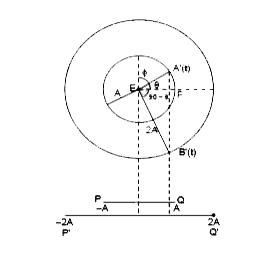
We solve the above problem with the help of phasor diagram. First we draw the initial position of both the particle on the phasor. From figure phase difference between both the particle is π/2.
They will meet each other when their projection from the circle on the horizontal diameter meet at one point.
Now from figure :
EF = A cos θ=2Asinθ
tan θ=12
θ−1(12)
So time taken by the particle to cross each other
t=angle travelled by Aω⇒t=π/2−θω

Topper's Solved these Questions
- SIMPLE HARONIC MOTION Book:MOTIONChapter:SIMPLE HARONIC MOTION Exercise:EXERCISE -1 ( SECTION-A )
Explore 8 Videos
- SIMPLE HARONIC MOTION Book:MOTIONChapter:SIMPLE HARONIC MOTION Exercise:EXERCISE -1 ( SECTION-B ) (Time per iod and angu larfrequency in SHM)
Explore 8 Videos
- SIMPLE HARMONIC MOTIONBook:MOTIONChapter:SIMPLE HARMONIC MOTIONExercise:EXERCISE -3 Section - B Previous Year Problems | JEE MAIN
Explore 23 Videos
- SOUND WAVESBook:MOTIONChapter:SOUND WAVESExercise:Exercise - 3 (Section - B)
Explore 14 Videos
Similar Questions
A particle executes SHM with a time period of 12s. Find the time taken by the particle to go directly from its mean position to half of its amplitude.
View SolutionA particle executes SHM with a time period of 4s. Find the time taken by the particle to go directly from its mean position to half of its amplitude.
View Solution
Knowledge Check
A particle executes SHM with a time period of 4 s . Find the time taken by the particle to go from its mean position to half of its amplitude . Assume motion of particle to start from mean position.
A1/3 sB2/3 sC4/3 sD5/3 sTwo particles execute SHM of the same time period along the same straight lines. They cross each other at the mean position while going in opposite directions. Their phase difference is
Aπ2BπC3π2D2πThe resultant of two S.H.M. having the same period T but different amplitudes and phases, along the same line is S.H.M
Ahaving a period 2TBhaving a period TChaving a period T/2Dhaving a period T4
A particle executed SHM iwht a time period of 3s and amplitude 6cm. Find (i) displacement (ii) velocity and (iii) acceleration, after 1/2 second, starting from the mean position.
View SolutionA particle executing S.H.M. starts from the mean position. Its phase, when it reaches the extreme position, is
View SolutionTwo particle of same time period (T) and amplitude undergo SHM along the same line with initial and phase of π/6. If they start at the same point along the opposite directions. Find the time other which they will meet again for the first time
View SolutionA particle executing a simple harmonic motion has a period of 6 s. The time taken by the particle to move from the mean position to half the amplitude, starting from the mean position is
View SolutionThe equation of S.H.M of a particle whose amplitude is 2 m and frequency 50 Hz. Start from extreme position is
View Solution

