Two partical AandB execute simple harmonic motion according to the equation y1=3sinωt and y2=4sin[ωt+(π/2)]+3sinωt. Find the phase difference between them.
A
π2
B
tan−1(45)
C
tan−1(34))
D
None of these
Video Solution
Text Solution
The correct Answer is:B
Representing a quantity with phase (ωt) along X-axis any quantity with a phase (ωt+ϕ) can be represented by a vector making an angle ϕ with a phase (ωt−ϕ) can be represented by a vector making an angle ϕ with x- axis in the clokwise sense
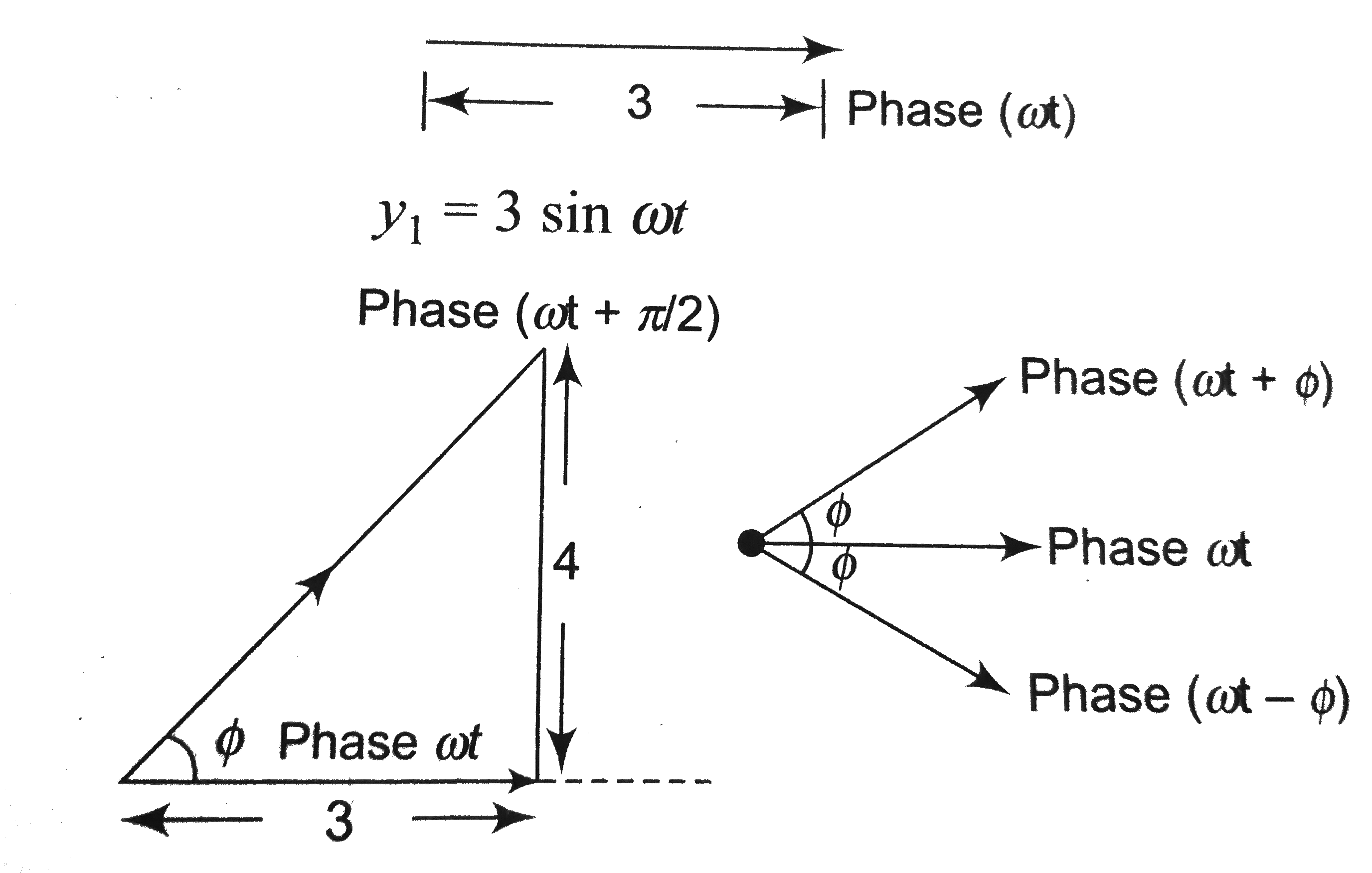
Phase difference ϕ=tan−1(45)
Altmetively given y1=3sinωt....(1)
And y2=4sin(ωt+π2)+3sinωt
=4cosωt+3sinωt=5[45cosωt+35sinωt]
=5[sinϕcosωt+cosωtsinωt]
=5sin(ωt+ϕ)

cosϕ=35sinϕ=45andtanϕ=45
From (i) and (ii) the result follows
|
Topper's Solved these Questions
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Problems Based On Mixed Concepts
24 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
22 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Simple Pendulum And Different Cases Of Shm
25 Videos
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test
30 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test
29 Videos
Similar Questions
Knowledge Check
The equations of two SH M's are
X1=4sin(ωt+π/2).X2=3sin(ωt+π)A6 unitsB5 unitsC1 unitsD7 unitsTwo waves are represented by the equations
y1=asin(ωt+kx+0.57)m and
y2=acos(ωt+kx)m,
where x is in metres and t is in seconds. The phase difference between them isA0.57 radianB1.0 radianC1.24 radianD1.57 radianTwo wave are represented by equation y1=asinωt and y2=acosωt the first wave :-
Aleads the second by πBlags the second by πCleads the second by π2Dlags the second by π2
Find the amplitude of the harmonic motion obtained by combining the motions
x1=(2.0cm)sinωt
and x2=(2.0cm)sin(ωt+π/3).
View SolutionTwo waves are represented by
y1=a1cos(ωt−kx) and
y2=a2sin(ωt−kx+π/3)
Then the phase difference between them is-
View SolutionTwo simple harmonic motions are represented by the equations y1=2(√3cos3πt+sin3πt) and y2=3sin(6πt+π6)
View SolutionTwo particle are executing simple harmonic motion. At an instant of time t their displacement are y1=acos(ωt) and y2=asin(ωt)
Then the phase difference between y1 and y2 is
View SolutionTwo sinusoidal current are given by
i1=20sin(ωt+π6)andi2=10sin(ωt−π4)
The pahase difference between them is
View Solution
