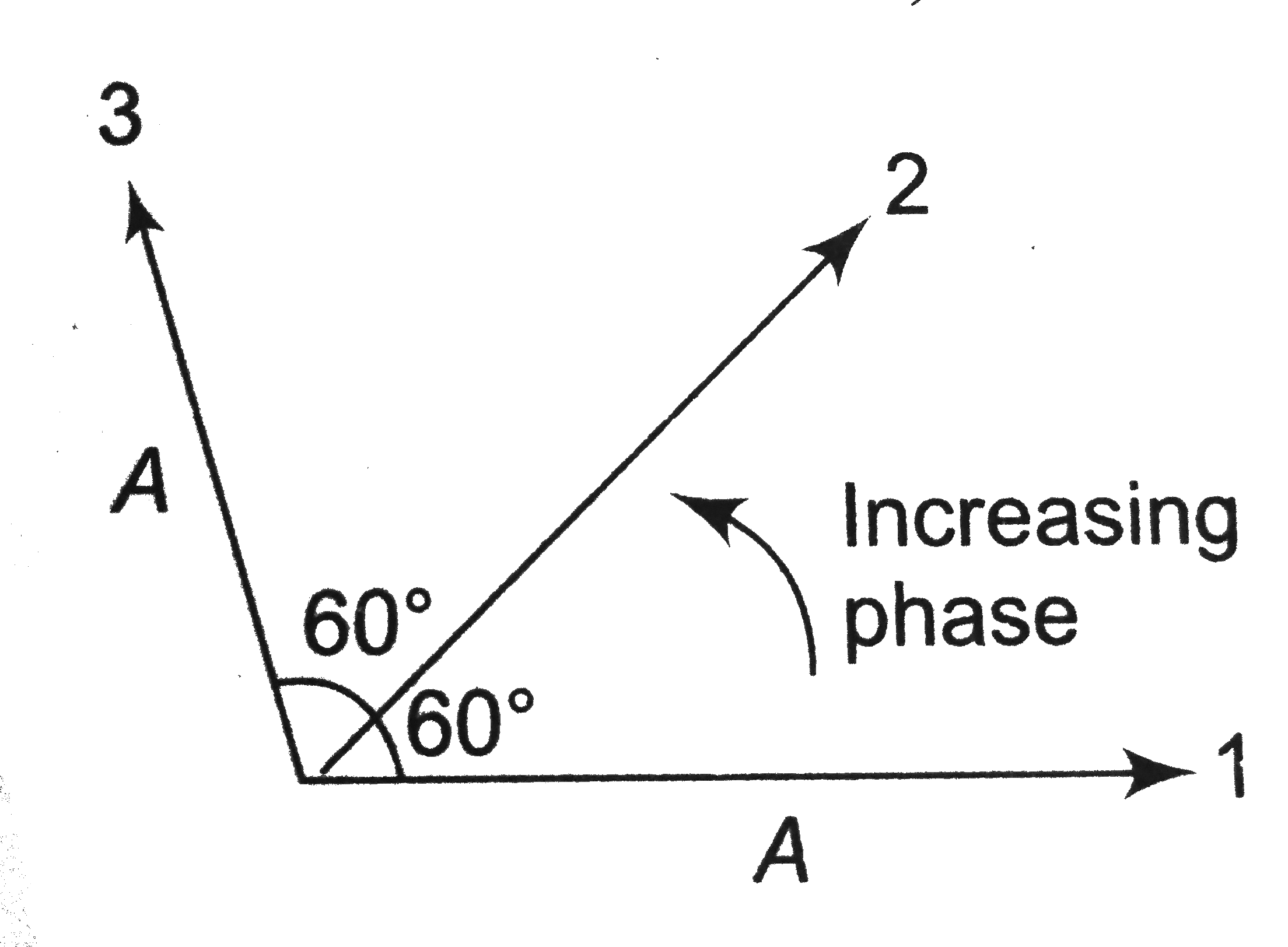
Three simple harmonic motion of equal amplitudes A and equal time peri

Time $S . H . M .$ of equal amplitude $a$ and equal time period in the same direction combine. The first is $60^{\circ}$ ahead of the second and second is $60^{\circ}$ ahead of the third $S . H . M$ . The amplitude of the resultant oscillation is:
Aa
B $2 a$
C0
D $4 a$
The equation of a simple harmonic motion (amplitude 5 cm and time period 0.5 second) is
Ay = 0.5 sin $2 π t$ ,
B $y = 0.5 \frac{sin (2 a t)}{5}$
C $y = 5 sin 4 π t$
D $y = 5 sin π t$
Three $S H O' s$ of equal amplitude $A$ and equal time period combine in the same direction. The difference in phase between successive $S H O' s$ os $60^{\circ}$ ahead of the other. The amplitude of the resultant oscillation is
A $A$
B $2 A$
C $0$
D $4 A$

Three simple harmonic motion of equal amplitudes $A$ and equal time periods in the same direction combine. The phase of the second motion is $60^{\circ}$ ahead of the first and the phase of the third motion is $60^{\circ}$ ahead of the second. Find the amplitude of the resultant motion.