Calculate the pressure inside a small air bubble of radus r situated at a depth h below the free surface of liquids of densities ρ1 and ρ2 and surface tennsions T1 and T2. The thickness of the first and second liquids are h1 and h2 respectively. Take atmosphere pressure =P0.

P0+ρ1gh1+ρ2g(h−h1)−2Tr
P0+ρ1gh1+ρ2g(h−h1)+2Tr
P0+ρ1gh2+ρ2g(h−h1)+2Tr
none of these
The correct Answer is:B
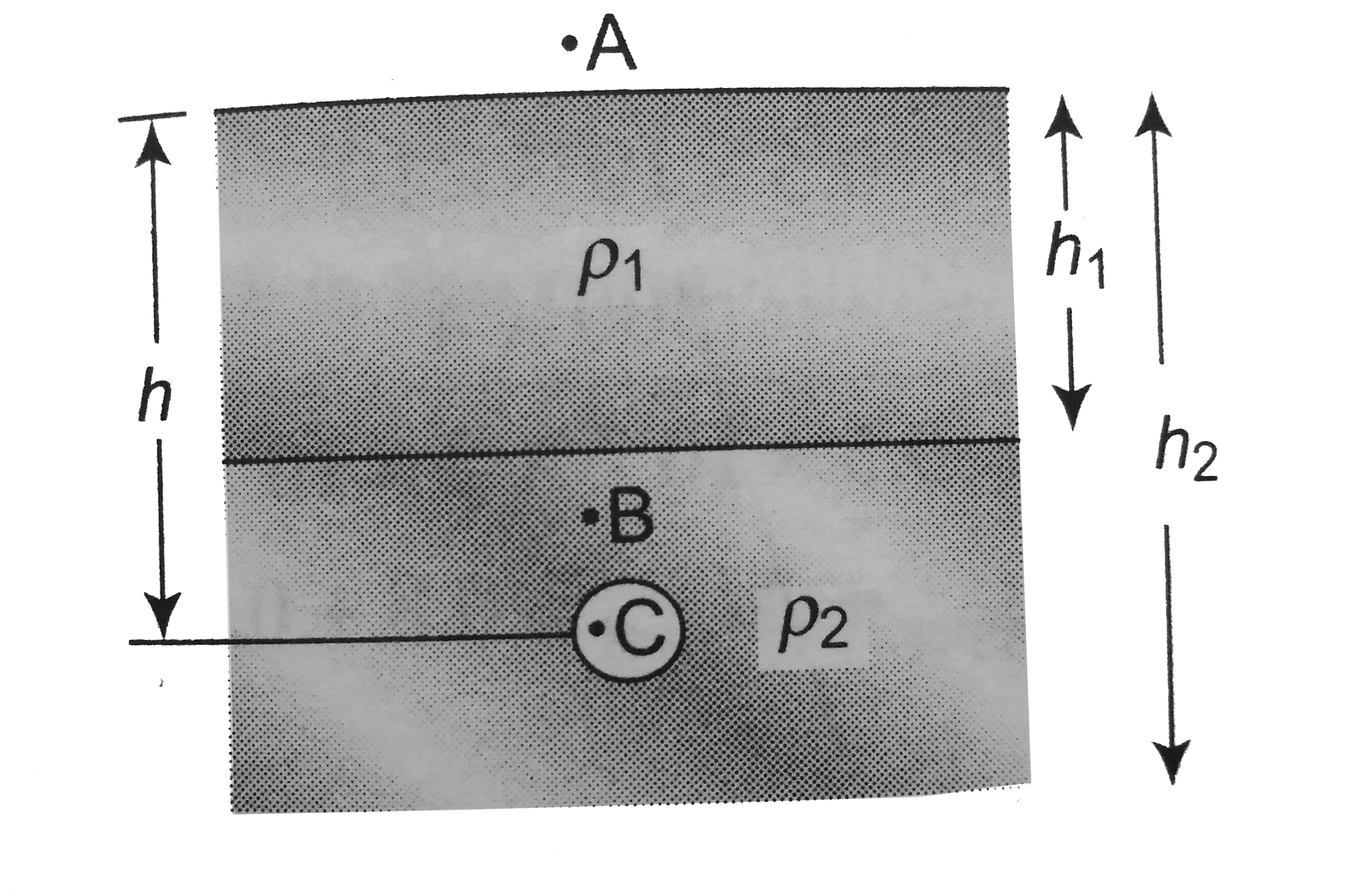
PC=PB+2Tr
PB=PA+ρ1gh1+ρ2g(h−h1)
where PA=P0
PC=P0+ρgh1+ρ2g(h−h1)+2Tr
Then evaluate by putting the numerical values,
Topper's Solved these Questions
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Assertion Reasoning
Explore 20 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:NEET Questions
Explore 17 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Viscosity
Explore 29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Chapter Test
Explore 29 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Chapter Test
Explore 29 Videos
Similar Questions
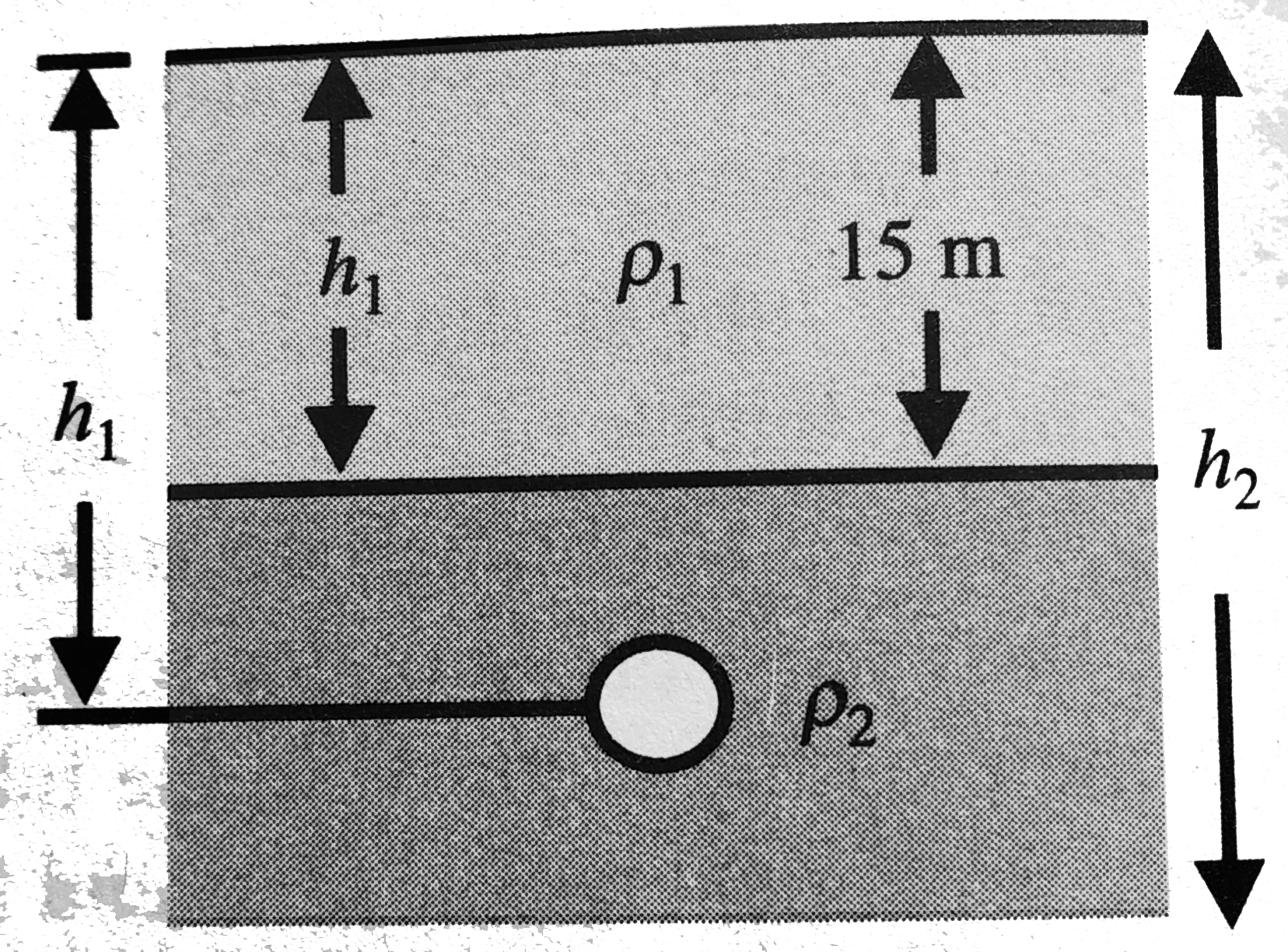
Calculate the pressure indise a small air bubble of radius 0.01mm situated at a depth of h=20m below the fre surface of liquid of density ρ1=103kg/m3,ρ2=800km/m3 and surface tension T2=7.5×10−2N/m. The thickness of the first liqid is h1=15m and h2=25m.
View SolutionWhat will be the total pressure inside a spherical air bubble of radius 0.2 mm at a depth of 2m below the surface of a liquid of density 1.1g/cm3 and surface tension 50dyne/cm. Atmospheric pressure is 1.01×105Nm−2.
View Solution
Knowledge Check
The pressure at depth h below the surface of a liquid of density ρ open to the atmosphere is
Agreater than the atmospheric pressure by ρghBless than the atmospheric pressure by ρghCequal to the atmospheric pressureDincreases exponentially with depthA small air bubble of radius 0.1 mm is situated at a depth of 10 m below the free surface of water .The external pressure on the bubble will be
A0.5×105N/m2B105N/m2C2×105N/m2D4×105N/m2If the atompspheric pressure is Pa then the jpressure P at depth a below the surface of a liquid of density ρ open to the atmosphere is
APa−ρgh2BPa−ρghCPa+ρghDP1+ρgh2
What should be the pressure inside a small air bubble of 0.1mm radius situated just below the water surface. Surface tension of water =7.2×10−2N/m and atmosphere pressure=1.013×105N/m2.
View SolutionA small air bubble of radius r in water is at depth h below the water surface. If P0 is the atmospheric pressure, ρ is the density of water and T is the surface tension of water, what is the pressure inside the bubble?
View SolutionA small air bubble of radius 'r' is at a depth 'h' below the water surface (density of water=ρ). Surface tension of water is T, atmospheric pressure is p0. Find pressure inside the air bubble for the condition r<<h
View SolutionThe pressure inside a small air bubble of radius 0.1mm situated just below the surface of water will be equal to [Take surface tension of water 70×10−3Nm−1 and atmospheric pressure=1.013×105Nm−2]
View SolutionThe absolute pressure at a depth h below the surface of a liquid of density ρ is [Given Pa = atmospheric pressure, g = acceleration due to gravity]
View Solution

