A man is rowing a boat with a constant velocity v0 in a river. The contact area of boat is 'A' and coefficient of viscosity is η. The depth of river is 'D' . Find the force required to row the boat.
ηAv02D
2ηAv0D
ηAv0D
3ηAv02D
The correct Answer is:C
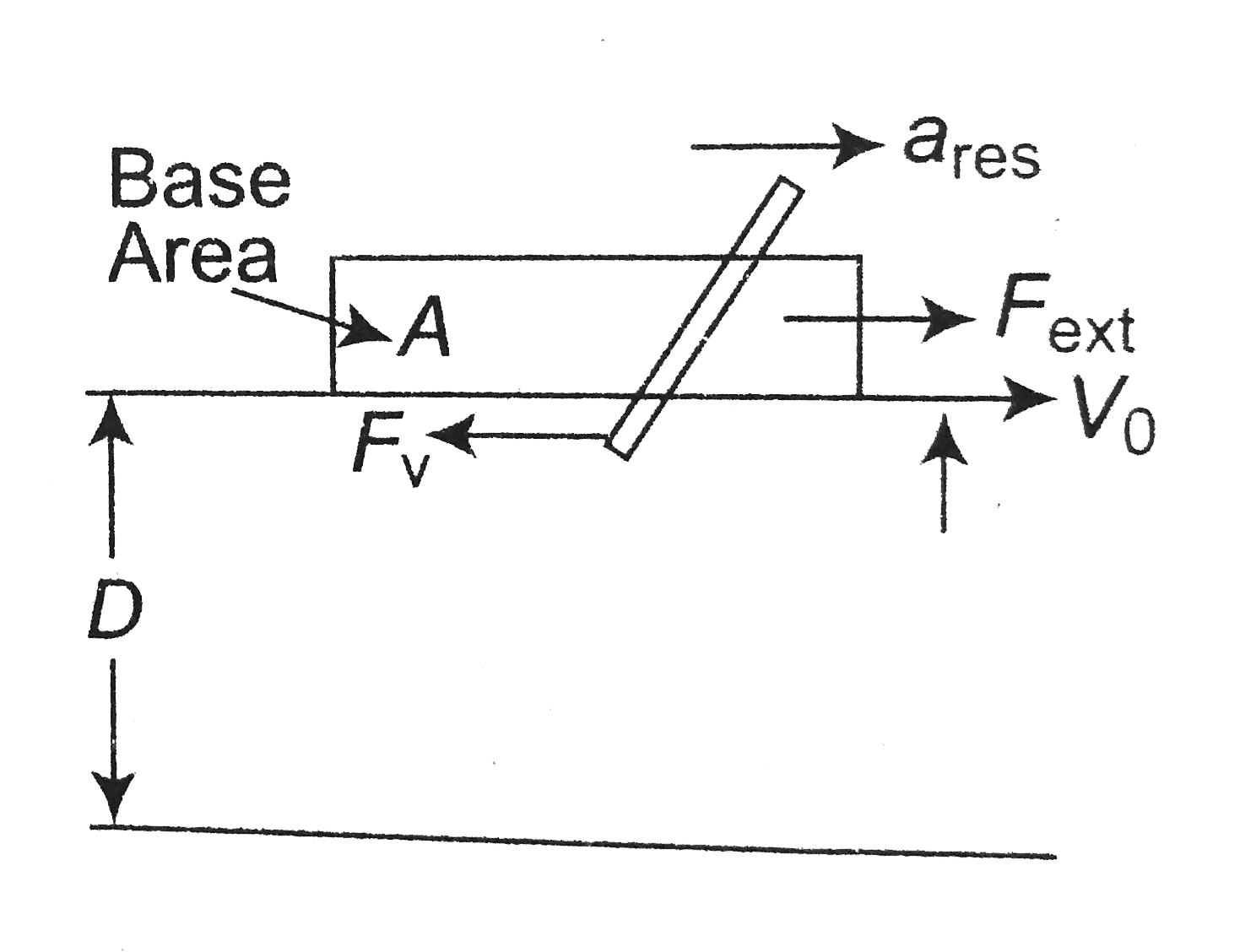
We can draw the free body diagram of boat
Fext=Fv=mares
As boat moves with constant velocity ares=0
Fext=Fv
But FV=ηAdvdz, but dvdz=v0−0D=v0D
then Fext=FV=ηAv0D
Topper's Solved these Questions
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Assertion Reasoning
Explore 20 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:NEET Questions
Explore 17 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Viscosity
Explore 29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Chapter Test
Explore 29 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Chapter Test
Explore 29 Videos
Similar Questions
A man starts rowing his stationary cuboidal boat of base area A=10m2. The driving force on the boat due to rowing is 100N in the direction of motion. Find the maximum velocity that the boat can achieve. Also find the time in which he will attain half of this maximum velocity. [ Take coefficient of viscosity of water =15 poise ] The depth of the lake is 10m and the combined mass of man and the boat to be 150kg.(u=0, velocity gradient uniform)
View SolutionRiver Man || River Boat Cases
View Solution
Knowledge Check
A boat crossing a river moves with a velocity v relative to still water. The river is flowing with a velocity v/2 with respect to the bank. The angle with respect to the flow direction with which the boat should move to minimize the drift is–
A30∘B60∘C150∘D120∘A man of mass m walks from end A to the other end B of a boat of mass M and length l. The coefficient of friction between the man and the boat is μ an neglect any resistive force between the boat and the water.
AIf the man runs at his maximum acceleration, the acceleration of the boat is (m/M)μg.BThe minimum time take by the man to reach the other end of the boat is √2MI(M+m)μgCIf man runs at his maximum acceleration the acceleration of boat is mm+MμgDThe minimum time take by the man to reach the other end of the boat is √2ml(M+m)μgA man is rowing a boat upstream and inspite of that the boat is found to be not moving with respect to the bank. The work done by the man is
AzeroBpositiveCnegativeDmay be +ve or −ve
The current velocity of river grows in proportion to the distance from its bank and reaches the maximum value v0 in the middle. Near the banks the velocity is zero. A boat is moving along the river in such a manner that the boatman rows his boat always perpendicular to the current. The speed of the boat in still water is u. Find the distance through which the boat crossing the river will be carried away by the current, if the width of the river is c. Also determine the trajectory of the boat.
View SolutionA man is standing on a straight bridge over a river and another man on a boat is on the river just below lthe man on the bridge. If the first man starts walking at the uniform speed of 4 m/ min and the boat moves perpendicularly to the bridge at the speed of 5 m/min then at what rate are they separating after 4 minutes if the height of the bridge above the boat is 3 m?
View SolutionA man wishes to cross a river which is flowing at a certain speed . Man uses a motor boat whose velocity with respect to water is more than speed of flow. Minimum possible time the boat takes to cross the river is t1 , but drift along the length of river is x . When boat takes shortest route to cross the river , then it takes time t2 . Find the velocity of boat with respect to water .
View SolutionA river is flowing towards with a velocity of 5ms−1. The boat velocity is 10ms−1. The boat crosses the river by shortest path. Hence,
View SolutionA boat moves relative to water with a velocity v and river is flowing with 2v. At what angle the boat shall move with the stream to have minimum drift?
View Solution

