Half of the recrtangular plate shown in figure is made of a material of density ρ1 and the other half of density ρ2. The length of the plate is L. Locate the centre of mass of the plate.
L2
(ρ1+3ρ2)4(ρ1+ρ2)L
(3ρ1+ρ2)(ρ1+ρ2)L
Mx=m(Lcosθ−x)
The correct Answer is:B
(b) Let area of each half is A and thickness of the plane is t
mass of left half =m1=ρ1 At, x1=L4
mass of right half=m2=ρ2 At, x2=3L4
Now apply xcm=m1x1+m2x2m1+m2=P1L+3P2L4(P1+P2).
Topper's Solved these Questions
Similar Questions
A square plate of edge d and a circular disc of diameter d are placed toucing ech other at the midpoint of san edge of th plate as shown in figure. Locate the centre of mass of the combination assuming same mass per unit area for the two plates.
View SolutionThe density of a linear rod of length L varies as ρ=A+Bx where x is the distance from the left end. Locate the centre of mass.
View Solution
Knowledge Check
Masses of 2kg each are placed at the corners B and A of a rectangular plate ABCD as shown in the figure. A mass of 8kg has to be placed on the plate so that the centre of mass of the system should be the centre O. Then the mass should be placed at :
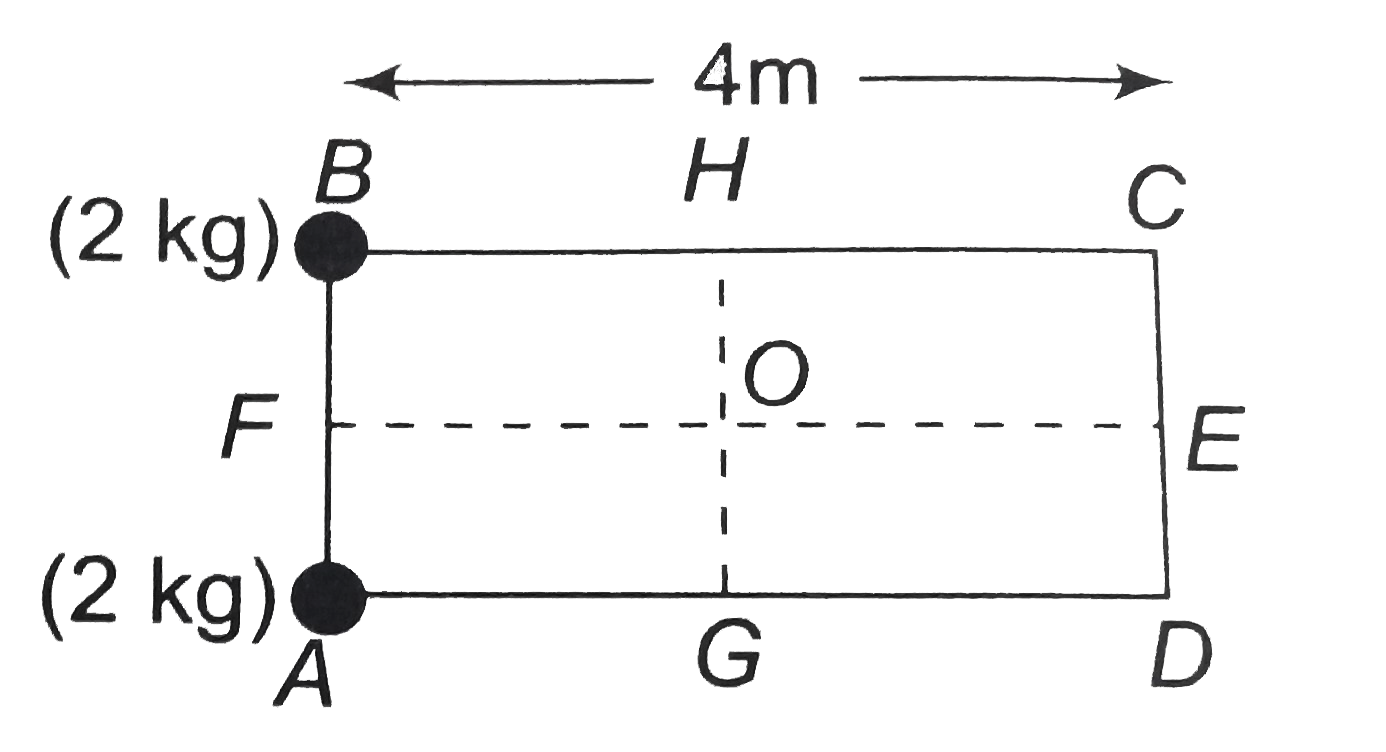.A1m from O onOEB2m from O on OFC2m from O on OGD2m from O on OHA circular plate of diameter d is kept in contact with a square plate of edge d as shown in figure. The densities of the material and the thickness are same
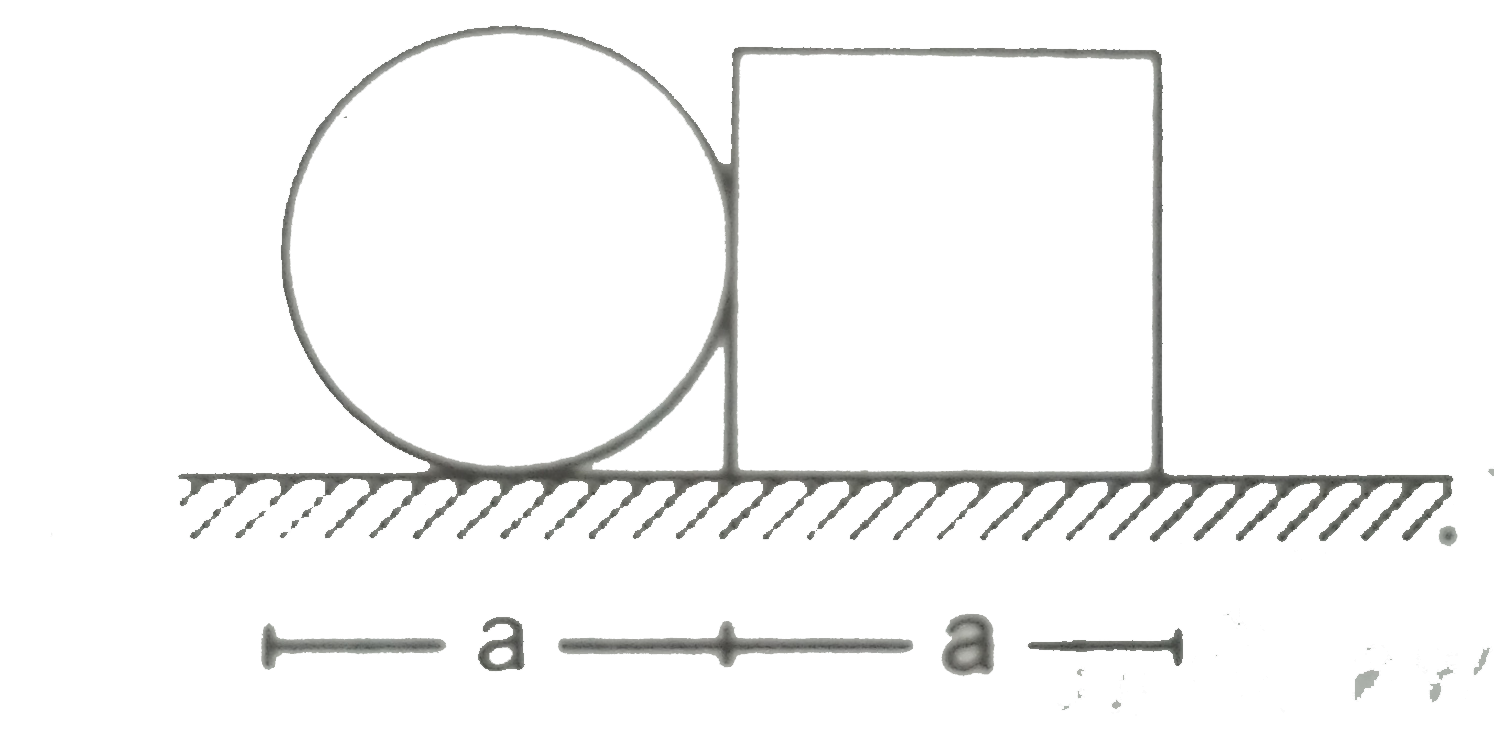. Everywhere. The centre of mass of the composite system will be Ainside the circular plateBinside hte square plateCat the point of contactDoutside the systemA circular plate of diameter a is kept in contact with a square plate of edge a as shown. The density of the material and the thickness are same everywhere. The centre of mass of the composite system will be
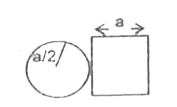Ainside the circular plateBinside the square plateCat the point of contactDoutside the system
A composite plate comprises a triangular area (1) and rectangular area (2) as shown in the figure. The triangular plate experiences forces due to the liquids of densities ρ1 and the rectangular plate experiences the force due to liquid of density ρ2. Find the hydrostatic forces on (a) area 1, (b) area 2, (c) total composite area of the plate. Assume ρ1=ρ and ρ2=2ρ.
View SolutionThe inductance L of a solenoid of length l, whose windings are made of material of density D and resistivity ρ, is (the winding resistance isR)
View SolutionIf two liquids of same mass but densities ρ1 and ρ2 respectively are mixed, then the density of the mixture is:
View SolutionIn a parallel -plate capacitor, the plates are kept vertical. The upper half of the space between the plates is filled with a dielectric with dielectric constant K and the lower half with a dielectric with dielectri constant K and the lower half with a dielectric with dielectric constant 2K. The ratio of the charge density on the upper half of the plates to the charge density on the lower half of the plates will be equal to
View SolutionIf two liquids of same volume but different densities ρ1 and ρ2 are mixed, then the density of the mixture is:
View Solution