A copper ball of mass m=1kg with a radius of r=10cm rotates with angular velocity ω=2rad/s about an axis passing through its centre. The work should be performed to increase the angular velocity of rotation of the ball two fold is.
1.2×10−2J
2.4×10−2J
3.6×10−2J
4.8×10−2J
The correct Answer is:B
(b) K.E.=12(25)mv2⇒K.E.=210mv2
If ω is to be doubled, v is also doubled.
Therefore, ΔK.E.=K.E.2−K.E.1=210m[v22−v21]
v=10−t=0ΔK.E.=210m[r2ω22−r2ω21]
=210×1[(110)2][42−22]=2.4×10−2J.
Topper's Solved these Questions
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Rotation And Translation Combined And Rolling Motion
Explore 18 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Problems Based On Mixed Concepts
Explore 31 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Angular Momentum And Its Conservation
Explore 30 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Chapter Test
Explore 29 Videos
- THERMAL PROPERTIES OF MATTERBook:A2ZChapter:THERMAL PROPERTIES OF MATTERExercise:Chapter Test
Explore 30 Videos
Similar Questions
A charge q is unifromly distributed over the volume of a unifrom ball of mass m and radius R which rotates with an angular velocity ω about the axis passing through its centre. Find the respective magnetic moment and its ratio to the mechanical moment.
View SolutionA uniform sphere of mass m=5.0kg and radius R=6.0cm rotates with an angular velocity ω=1250rad/s about a horizontal axle passing through its centre and fixed on the mounting base by means of bearings. The distance between the bearings equals l=15cm. The base is set in rotation about a vertical axis with an angular velocity ω′=5.0rad/s. Find the modulus and direction of the gyroscopic forces.
View Solution
Knowledge Check
A ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with angular velocity ω. Its kinetic energy is
A12mr2ω2Bmrω2Cmr2ω2D12mrω2A ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with angular velocity ω. Its kinetic energy is
A12mr2ω2Bmrω2Cmr2ω2D13mr2ω2A horizontal disk is rotating with angular velocity ω about a vertical axis passing through its centre. A ball is placed at the centre of groove and pushed slightly. The velocity of the ball when it comes out of the groove -
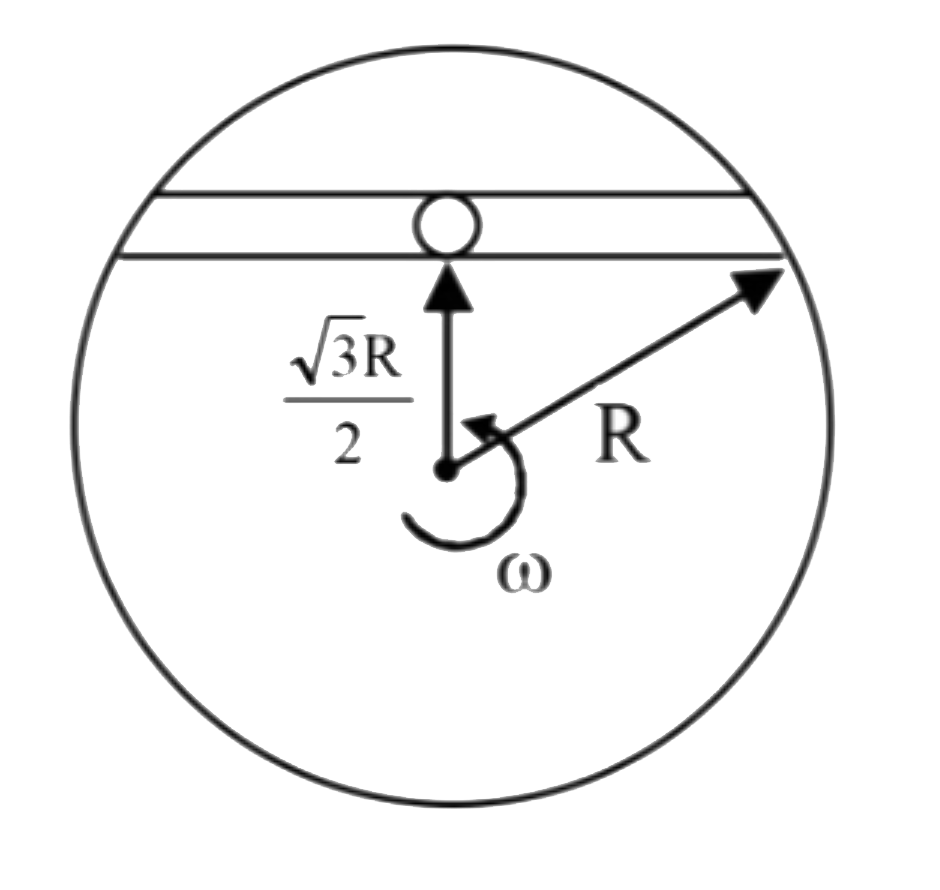 A√32ωRBωR2CωRDωR√2
A√32ωRBωR2CωRDωR√2
A disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionA circular disc of mass 2 kg and radius 0.1 m is rotating at an angular speed of 2 rad/s, about an axis passing through its centre and perpendicular to its plane. What is its rotational kinetic energy?
View SolutionA rigid body of mass m rotates with angular velocity ω about an axis at a distance a from the centre of mass G. The radius of gyration about a parallel axis through G is k. The kinetic energy of rotation of the body is
View SolutionA rigid body of mass m rotates about an axis passing through its centre. If the angular velocity of the body is unity, the moment of inertia of the body will be equal to
View SolutionA rigid body of mass m rotates about an axis passing through its centre. If the angular velocity of the body is unity, the moment of inertia of the body will be equal to
View Solution

