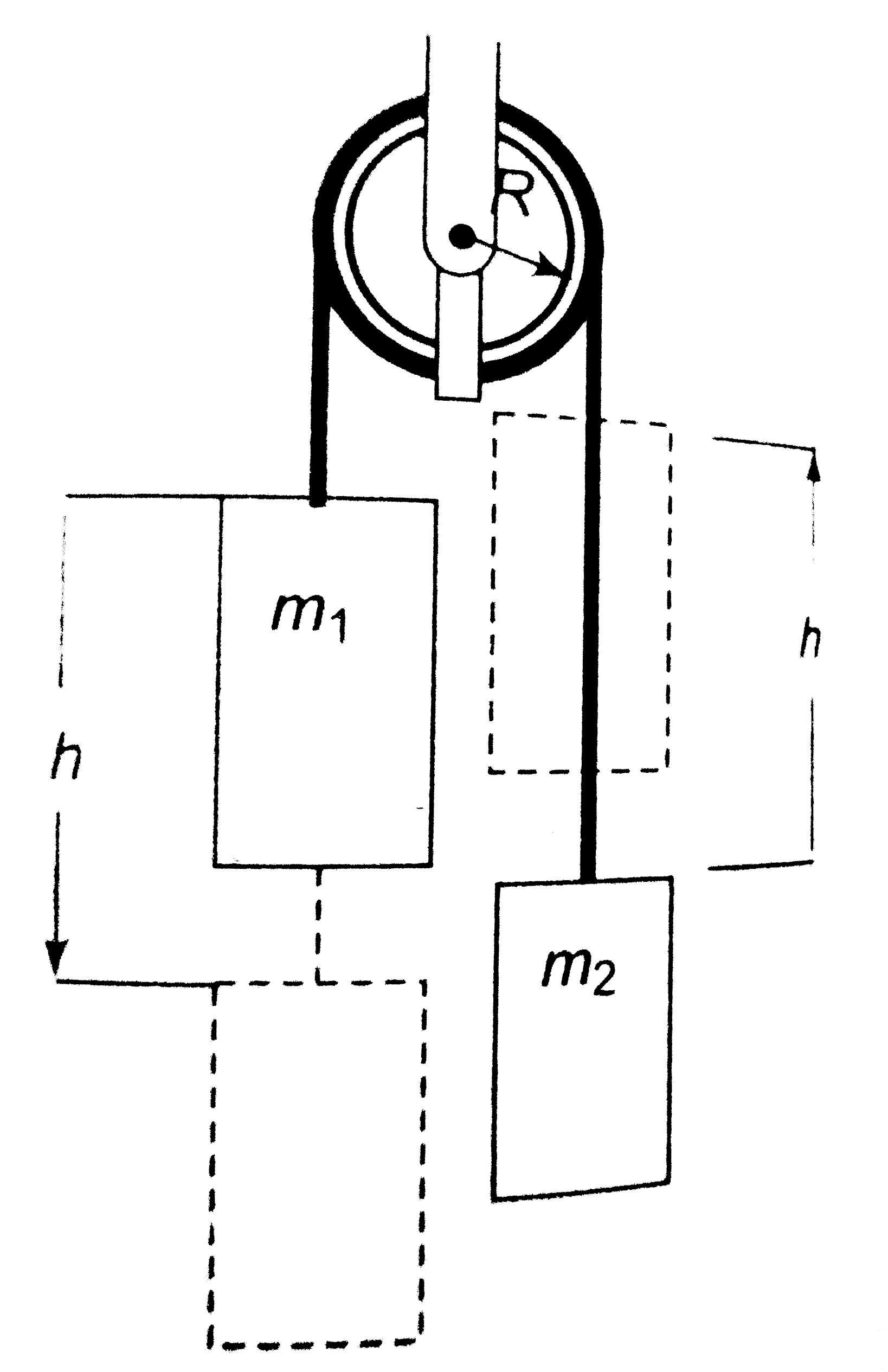
Consider two object with m1>m2 connected by a light string that passes over a pulley having a moment of inertia of I about its axis of rotation as shown in figure. The string does not slip on the pulley or strech. The pulley turns without friction. The two objects are released from rest separated by a vertical distance 2h. The translational speeds of the objects as they pass each other is.
 .
.
⎷2(m1+m2)ghm1+m2+IR2
⎷2(m1−m2)ghm1+m2+IR2
⎷(m1−m2)ghm1+m2+IR2
⎷(m1+m2)ghm1+m2+IR2
The correct Answer is:B
(b) Take the two objects pulley, and Earth as the system. If we neglect friction in the system, then mechanical energy is conserved and we can state that the increase in kinetic energy of the system equals the decrease in potential energy. Since Ki=0(the system is initially at rest). we have
ΔK=Kf=Ki
=12m1v2+12m2v2+12Iω2
where m1 and m2 have a common speed. But
v=Rω so that ΔK=12(m1+m2+IR2)V2
From FIG. we see that the system loses potential energy because of the motion of m1 and gains potential energy because of the motion of m2. Applying the law of conservation of energy,
ΔK+ΔU=0, gives
12(m1+m2+IR2)v2+m2gh−m1gh=0
v=
⎷2(m1−m2)ghm1+m2+IR2.
Topper's Solved these Questions
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Rotation And Translation Combined And Rolling Motion
Explore 18 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Problems Based On Mixed Concepts
Explore 31 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Angular Momentum And Its Conservation
Explore 30 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Chapter Test
Explore 29 Videos
- THERMAL PROPERTIES OF MATTERBook:A2ZChapter:THERMAL PROPERTIES OF MATTERExercise:Chapter Test
Explore 30 Videos
Similar Questions
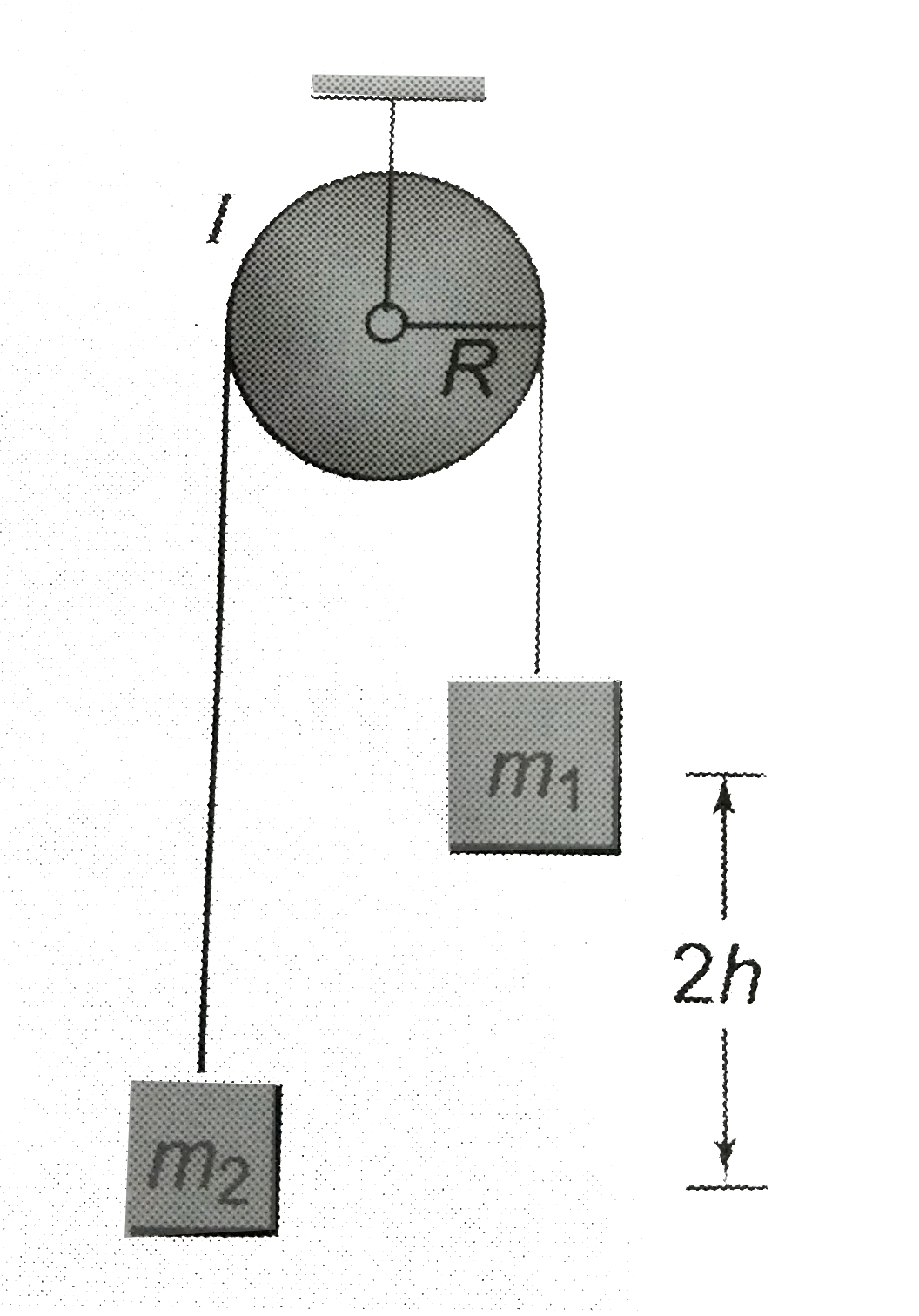
Consider the situation as shown in the figure. If m1>m2, I is the moment of intertia about its axis of rotation, R is the radius of pulley. The objects are released from rest separated by a vertical distance 2h. Find the translational speed of the objects as they pass each other. Assume no slipping.
View SolutionSolve the previous problem if the pulley has a moment of inertia I about its axis and the string does not slip over it.
View Solution
Knowledge Check
Consider two masses with m1>m2 connected by a light inextensible string that passes over a pulley of radius R and moment of inertia I about its axis of rotation. The string does not slip on the pulley and the pulley turns without friction. The two masses are released from rest separated by a vertical distance 2h. When the two masses pass each other, the speed of the masses is proportional to
A ⎷m1−m2m1+m2+1R2B ⎷(m1−m2)(m1−m2)m1+m2+1R2C ⎷m1+m2+1R2m1−m2D ⎷1R2m1+m2Two masses M and m(M>m) are joined by a light string passing over a smooth light pulley.
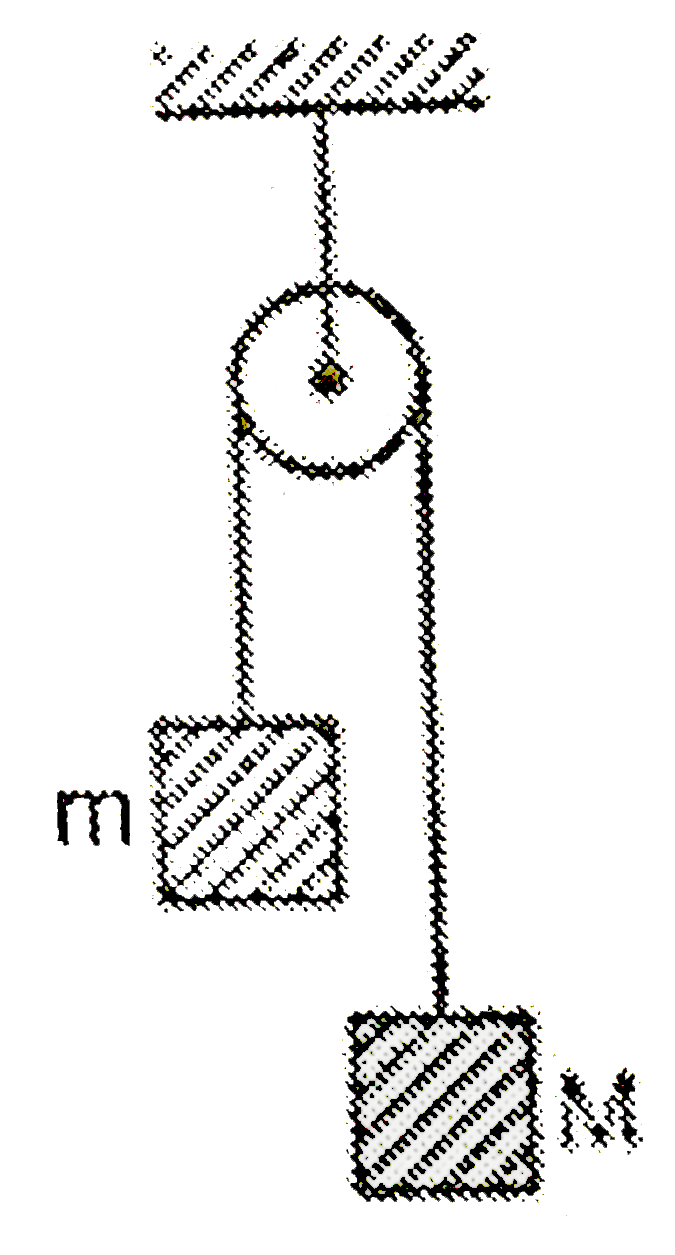 AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)g
AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)gTwo blocks A and B , each of mass 10kg , are connected by a light string passing over a smooth pulley as shown in the figure. Block A will remain at rest if the friction on it is
 A50N up the planeB50N down the planeC100N up the planeD100N down the plane
A50N up the planeB50N down the planeC100N up the planeD100N down the plane
In the figure, the massless and inextensible thread does not slip on the pulley. It is wound over pulley as shown. If the system is released from rest,
View SolutionA block of mass m hangs by means of a string which goes over a pulley of mass m and moment of inertia l, as shown in the diagram. The string does not relative to the pulley. Find the frequency of small oscillations.
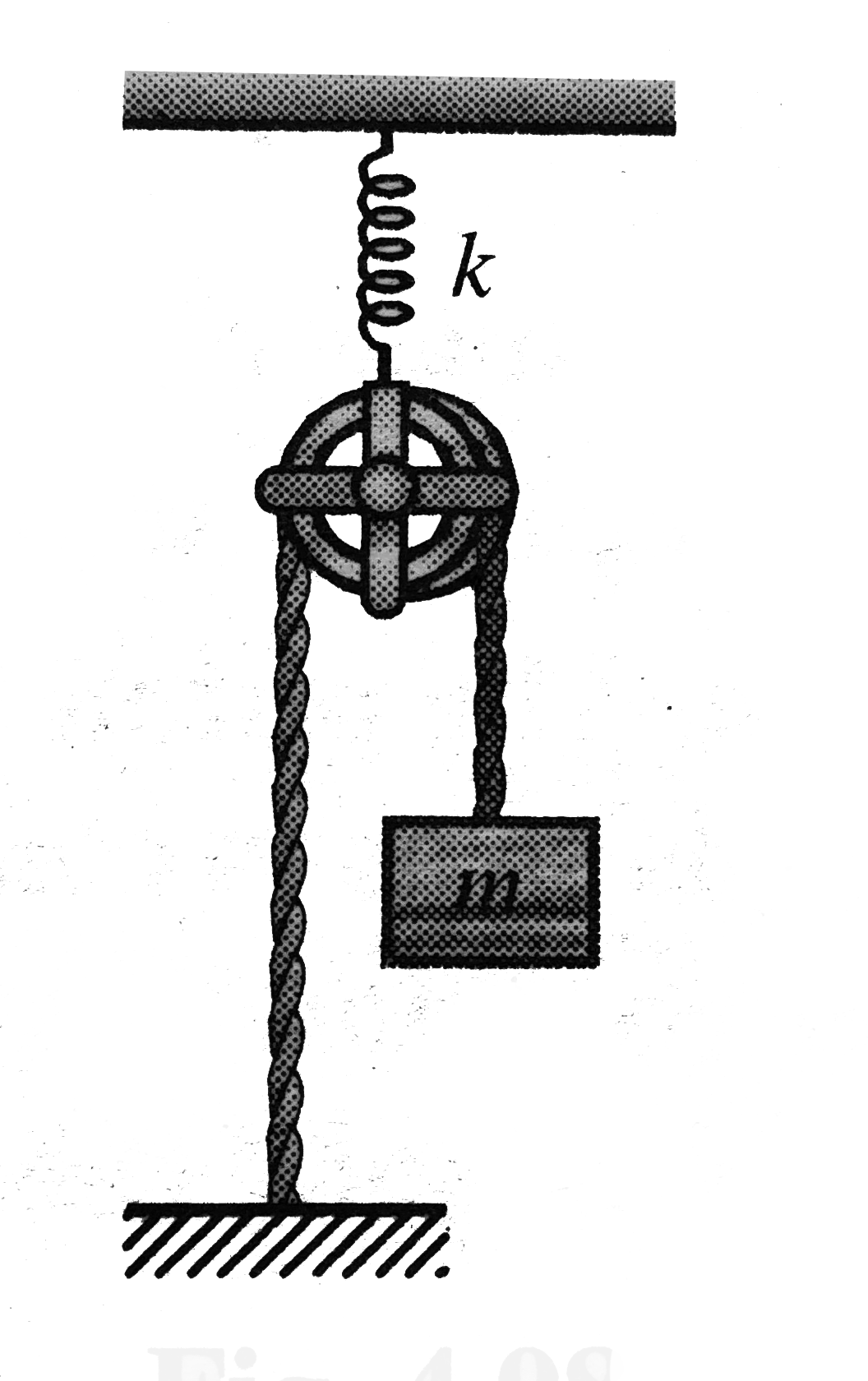
View SolutionAn object of mass m is tied to a light string wound around a pulley that has a moment of inertia I and radius R. The wheel bearing is fricrtionless and the string does not slip on the run. Find the tension in the string and the acceleration of the object.
View SolutionTwo blocks are connected by an inextensible light string, the string is passing over smooth, light pulley as shown. Find the acceleration of blocks and tension in the string, reaction in pulley.

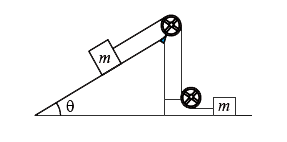
View SolutionTwo blocks each of mass m are connected over two light and frictionless pulleys and a fixed wedge by a light string as shown in figure. The tension in the string is :
View Solution

