A wagon of 200kg is moving on a smooth track with velocity of 2m/sec. A man of 80kg also runs in the wagon with a velocity such that speed of the centre of mass of the system is zero. Find the velocity of man relative to the wagon (in m//s).
5
6
7
8
The correct Answer is:C
To solve the problem, we need to find the velocity of the man relative to the wagon, given that the velocity of the center of mass of the system (wagon + man) is zero.
1. Identify the masses and velocities:
- Mass of the wagon, mw=200kg
- Velocity of the wagon, vw=2m/s
- Mass of the man, mm=80kg
- Velocity of the man, vm (unknown)
2. Use the formula for the velocity of the center of mass (COM):
The velocity of the center of mass vcm of the system is given by:
vcm=mw⋅vw+mm⋅vmmw+mm
We know that vcm=0 (as given in the problem).
3. Set up the equation:
Substituting the known values into the equation:
0=200⋅2+80⋅vm200+80
This simplifies to:
0=400+80vm280
Multiplying both sides by 280 gives:
0=400+80vm
4. Solve for vm:
Rearranging the equation:
80vm=−400
Dividing both sides by 80:
vm=−5m/s
5. Find the velocity of the man relative to the wagon:
The velocity of the man relative to the wagon vm,relative is given by:
vm,relative=vm−vw
Substituting the values we found:
vm,relative=−5−2=−7m/s
Final Answer:
The velocity of the man relative to the wagon is −7m/s.
---
- Mass of the wagon, mw=200kg
- Velocity of the wagon, vw=2m/s
- Mass of the man, mm=80kg
- Velocity of the man, vm (unknown)
The velocity of the center of mass vcm of the system is given by:
vcm=mw⋅vw+mm⋅vmmw+mm
We know that vcm=0 (as given in the problem).
Substituting the known values into the equation:
0=200⋅2+80⋅vm200+80
This simplifies to:
0=400+80vm280
Multiplying both sides by 280 gives:
0=400+80vm
Rearranging the equation:
80vm=−400
Dividing both sides by 80:
vm=−5m/s
The velocity of the man relative to the wagon vm,relative is given by:
vm,relative=vm−vw
Substituting the values we found:
vm,relative=−5−2=−7m/s
The velocity of the man relative to the wagon is −7m/s.
Topper's Solved these Questions
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Moment Of Inertia
Explore 39 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Rotational Kinematics
Explore 19 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Chapter Test
Explore 29 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Chapter Test
Explore 29 Videos
- THERMAL PROPERTIES OF MATTERBook:A2ZChapter:THERMAL PROPERTIES OF MATTERExercise:Chapter Test
Explore 30 Videos
Similar Questions
Knowledge Check
Two particles of mass 1 kg and 0.5 kg are moving in the same direction with speed of 2m/s and 6 m/s respectively on a smooth horizontal surface. The speed of centre of mass of the system is
A103m/sB107m/sC112m/sD123m/sA wagon weighing 1000 kg is moving with a velocity 50 km/h on smooth horizontal rails. A mass of 250 kg is dropped into it. The velocity with which it moves now is
A2.5km/hourB20 km/hourC40 km/hourD50 km/hourTwo bodies of masses 1kgand2kg are moving in two perpendicular direction with velocities 1m/sand2m/s as shown in figure. The velocity of the centre of mass (in magnitide) of the system will be :
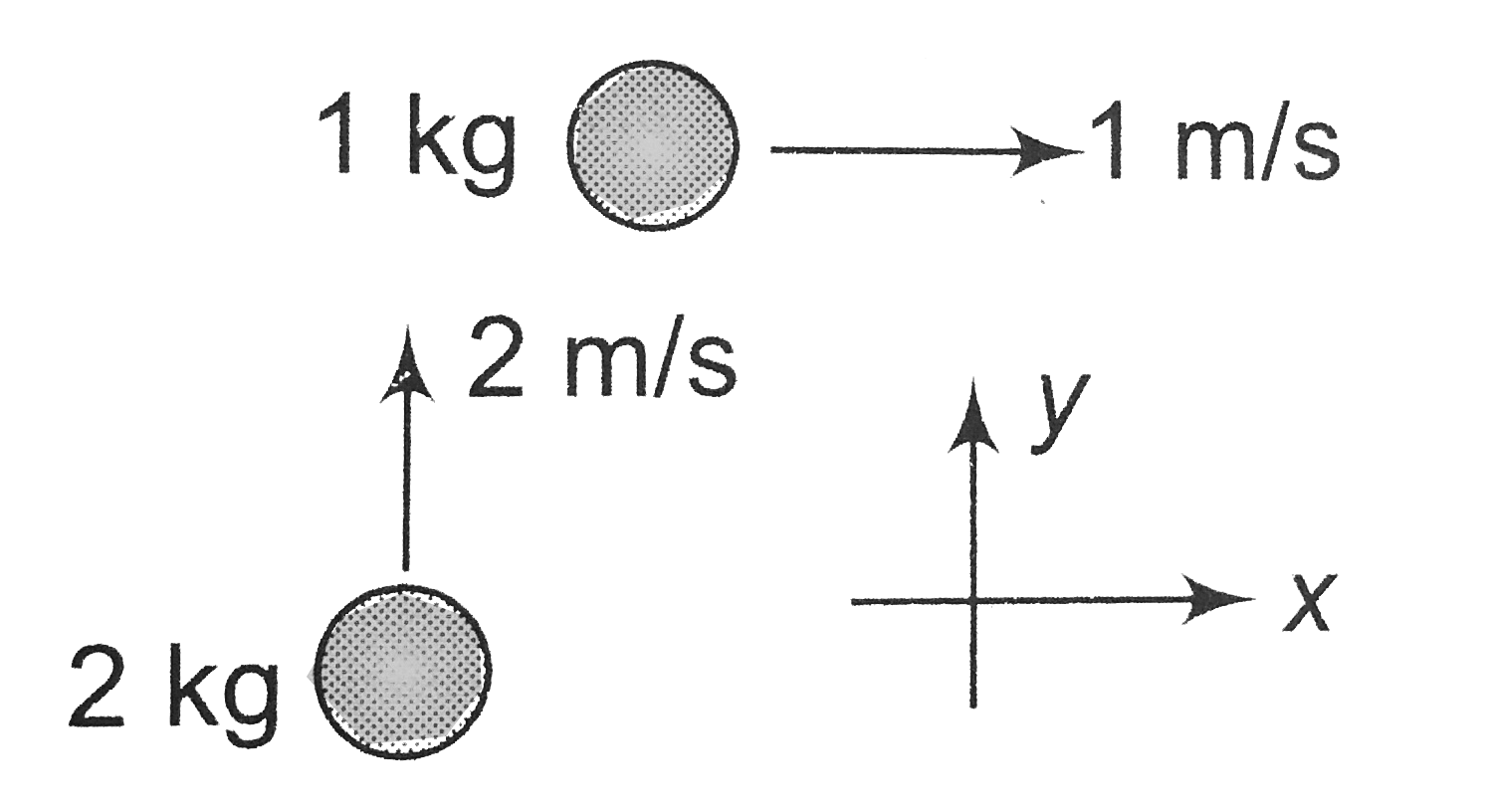 A3m/sB1.67m/sC1.5m/sD1.37m/s
A3m/sB1.67m/sC1.5m/sD1.37m/s
Rain is falling vertically downward with velocity 4m/s. A man is moving horizontally with velocity 3m/s, the velocity of rain with respect to man is
View SolutionA train is running at 5m/s and a man jumps out of it with a velocity 10m/s in a direction making an angle of 60∘ with the direction of the train. The velocity of the man relative to the ground is equal to :
View SolutionA train is running at 5m/s and a man jumps out of it with a velocity 10m/s in a direction making an angle of 60∘ with the direction of the train. The velocity of the man relative to the ground is equal to :
View SolutionA ship is moving due east with a velocity of 12m/sec, a truck is moving across on the ship with velocity 4m/sec.A monkey is climbing the vertical pole mounted on the truck with a velocity of 3m/sec.Find the velocity of the monkey as observed by the man on the shore (m/sec)
View SolutionA boat of mass 50kg is at rest. A dog of mass 5kg moves in the boat with a velocity of 20m/s. What is the velocity of boat?
View Solution
