A boat of mass 1000 kg is moving with a velocity of 5 m/s. A person of mass 60 kg jumps into the boat. The velocity of the boat with the person will be -
4.71m/s
4.71cm/s
47.1m/s
47.1cm/s
To solve the problem of a boat with a person jumping into it, we will use the principle of conservation of momentum. Here’s a step-by-step solution:
Step 1: Identify the masses and initial velocities
- Mass of the boat (m_boat) = 1000 kg
- Initial velocity of the boat (v_boat_initial) = 5 m/s
- Mass of the person (m_person) = 60 kg
- Initial velocity of the person (v_person_initial) = 0 m/s (since the person is initially at rest)
Step 2: Calculate the initial momentum
The initial momentum (P_initial) of the system (boat + person) can be calculated as follows:
Pinitial=(mboat×vboat\_initial)+(mperson×vperson\_initial)
Substituting the values:
Pinitial=(1000kg×5m/s)+(60kg×0m/s)
Pinitial=5000kg m/s+0
Pinitial=5000kg m/s
Step 3: Calculate the final momentum
After the person jumps into the boat, the total mass of the system becomes:
mtotal=mboat+mperson=1000kg+60kg=1060kg
Let the final velocity of the boat with the person be vf. The final momentum (P_final) can be expressed as:
Pfinal=mtotal×vf=1060kg×vf
Step 4: Apply conservation of momentum
According to the law of conservation of momentum:
Pinitial=Pfinal
Substituting the values we calculated:
5000kg m/s=1060kg×vf
Step 5: Solve for the final velocity (v_f)
Now, we can solve for vf:
vf=5000kg m/s1060kg
Calculating this gives:
vf≈4.72m/s
Conclusion
The final velocity of the boat with the person is approximately 4.72 m/s.
---
- Mass of the boat (m_boat) = 1000 kg
- Initial velocity of the boat (v_boat_initial) = 5 m/s
- Mass of the person (m_person) = 60 kg
- Initial velocity of the person (v_person_initial) = 0 m/s (since the person is initially at rest)
The initial momentum (P_initial) of the system (boat + person) can be calculated as follows:
Pinitial=(mboat×vboat\_initial)+(mperson×vperson\_initial)
Substituting the values:
Pinitial=(1000kg×5m/s)+(60kg×0m/s)
Pinitial=5000kg m/s+0
Pinitial=5000kg m/s
After the person jumps into the boat, the total mass of the system becomes:
mtotal=mboat+mperson=1000kg+60kg=1060kg
Let the final velocity of the boat with the person be vf. The final momentum (P_final) can be expressed as:
Pfinal=mtotal×vf=1060kg×vf
According to the law of conservation of momentum:
Pinitial=Pfinal
Substituting the values we calculated:
5000kg m/s=1060kg×vf
Now, we can solve for vf:
vf=5000kg m/s1060kg
Calculating this gives:
vf≈4.72m/s
The final velocity of the boat with the person is approximately 4.72 m/s.
Topper's Solved these Questions
Similar Questions
A boat of 90kg is floating in still water. A boy of mass 30 kg walks from the stern to the bow. The length of the boat is 3 m. Calculate the distance through which the boat will move.
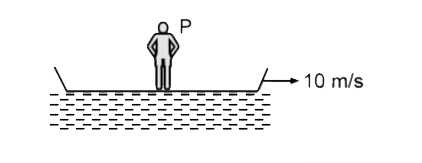
View SolutionA person P of mass 50 kg stands at the middle of a boat of mass 100 kg moving at a constant velocity 10 m/s with no friction between water and boat and also the engine of the boat is shut off. With what velocity (relative to the boat surface) should the person move so that the boat comes to rest. Neglect friction between water and boat.
View Solution
Knowledge Check
A person of mass 70 kg jump from a 3.0m height
AImpulse on the main by ground will be 539N−sBaverage force on man if the landing is with stiffed leg and body moves by 1.0cm during impact is 2.1×105NCaverage force on man feet by ground if he land with bent legs and body moves by 50cm is 4.2×103NDaverage force on man feet by ground if he land with bent legs and body moves by 50cm is (4.9×103N)A boat of mass 50kg is at rest. A dog of mass 5kg moves in the boat with a velocity of 20m/s. What is the velocity of boat?
A4m/sB2m/sC8m/sD1m/sA boat of mass 40kg is at rest. A dog of mass 4kg moves in the boat with a velocity of 10m/s. What is the velocity of boat (nearly)?
A4m/sB2m/sC8m/sD1m/s
A motor boat is travelling with a speed of 3.0m / sec . If the force on it due to water flow is 500 N , the power of the boat is
View SolutionA boat crosses a river with a velocity of 8kmh. If the resulting velocity of boat is 10kmh then the velocity of river water is
View SolutionA boat is moving with a velocity 2i + 3j with respect to ground. The water in the river is moving with a velocity -2i - 3j with respect to ground. The relative velocity of the boat with respect to water is
View SolutionA boat is moving with a velocity 3ˆi+4ˆj with respect to ground. The water in the river is moving with a velocity −3ˆi−4ˆj with respect to ground. The relative velocity of the boat with respect to water is.
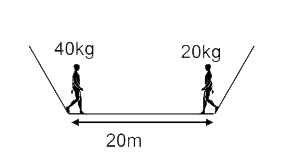
View SolutionTwo men of masses 40 kg and 20 kg are standing on a boat of mass 100 kg. Length of boat is 20m. Neglect the friction between water and boat. Find the displacement of the boat when both the persons reach at middle of boat.
View Solution

