In order to raise a mass of 100kg a of mass 60kg fastens a rope to it and passes the rope over a smooth pulley. He climbs the rope with acceleration 5g/4 relative to the rope. The tension in the rope is: Take g=10m/s2
1432N
928N
1219N
642N
The correct Answer is:C
To solve the problem, we will analyze the forces acting on both the man and the mass he is trying to lift, and use Newton's second law of motion to derive the tension in the rope.
Step 1: Identify the given values
- Mass of the man (m1) = 60 kg
- Mass to be lifted (m2) = 100 kg
- Acceleration of the man relative to the rope (a_rel) = 5g4
- Acceleration due to gravity (g) = 10 m/s²
Step 2: Calculate the absolute acceleration of the man
Let the acceleration of the rope (and the mass being lifted) be A. The absolute acceleration of the man (a_m) can be expressed as:
am=arel+A
Substituting the values:
am=5g4+A
Step 3: Write the equations of motion for the man and the mass
For the man climbing the rope:
Using Newton's second law,
T−m1g=m1am
Substituting am:
T−60g=60(5g4+A)
T−600=75g+60A
(1) T=600+75g+60A
For the mass being lifted:
Using Newton's second law,
T−m2g=m2A
Substituting the values:
T−100g=100A
(2) T=100g+100A
Step 4: Set the equations for T equal to each other
From equations (1) and (2):
600+75g+60A=100g+100A
Step 5: Rearrange to solve for A
Rearranging gives:
600+75g−100g=100A−60A
600−25g=40A
Substituting g=10:
600−250=40A
350=40A
A=35040=8.75m/s2
Step 6: Substitute A back to find T
Now substitute A back into equation (2) to find T:
T=100g+100A
T=100(10)+100(8.75)
T=1000+875
T=1875N
Conclusion
The tension in the rope is T=1875N.
---
- Mass of the man (m1) = 60 kg
- Mass to be lifted (m2) = 100 kg
- Acceleration of the man relative to the rope (a_rel) = 5g4
- Acceleration due to gravity (g) = 10 m/s²
Let the acceleration of the rope (and the mass being lifted) be A. The absolute acceleration of the man (a_m) can be expressed as:
am=arel+A
Substituting the values:
am=5g4+A
For the man climbing the rope:
Using Newton's second law,
T−m1g=m1am
Substituting am:
T−60g=60(5g4+A)
T−600=75g+60A
(1) T=600+75g+60A
Using Newton's second law,
T−m2g=m2A
Substituting the values:
T−100g=100A
(2) T=100g+100A
From equations (1) and (2):
600+75g+60A=100g+100A
Rearranging gives:
600+75g−100g=100A−60A
600−25g=40A
Substituting g=10:
600−250=40A
350=40A
A=35040=8.75m/s2
Now substitute A back into equation (2) to find T:
T=100g+100A
T=100(10)+100(8.75)
T=1000+875
T=1875N
The tension in the rope is T=1875N.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Basic Concept Of Static And Kinetic Frictions
Explore 45 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Dynamics Of Circular Motion
Explore 31 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Equilibrium Of A Particle
Explore 19 Videos
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Chapter Test
Explore 29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Chapter Test
Explore 29 Videos
Similar Questions
A man of 80 kg fastns a rope to a mass of 120kg, and passes the rope over a smooth pulley. In order to raise it up he climbs the riope with acceleration 3g2 relative to the rope. Calculate the tension in the rope in N. (Take g=10m/s2)
View SolutionTo raise a weight which is half as much again as his weight a man fastens a rope to it and passes over a smooth pulley, he then climbs up the rope with an acceleration 6g7 relative to the rope. Show that the weight rises with acceleration 87, and find the tension of the rope.
View Solution
Knowledge Check
In order to raise a mass of 100 kg, a man of mass 60 kg fastens a rope to it and passes the rope over a smooth pulley. He climbs the rope with acceleration 5g/4 relative to the rope. The tension in the rope is (take g=10ms−2)
 A48758NB48752NC48754ND48756N
A48758NB48752NC48754ND48756NIn order to raise a mass of 100kg a man of mass 60kg fastens a rope to it and passes the rope over a smooth pulley. He climbs the rope with acceleration 5g/4 relative to the rope. The tension in the rope is: Take g=10m/s2
A1432NB928NC1218ND642NAn object of mass 5 kg is attached to the end ofa rope. If the rope is pulled upward with an acceleration 0.30ms−2, what is the tension in the rope?
A30.5 NB40.5 NC50.5 ND60.5 N
A boy of mass 40kg climbs up a rope with an acceleration of 1.2ms−2.What is the tension in the rope?
View SolutionTension in the rope at the rigid support is (g=10m/s2)
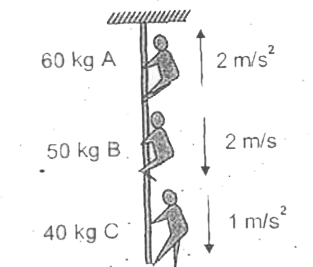
View SolutionTow men of masses m1andm2 hold on the opposite ends of a rope passing over a frictionless pulley. The men m1 climbs up the pore with an acceleration of 1.2m/s2 relative to the rope. The mann m2 climbs up the rope with an acceleration of 2m/s2 relative to the rope. Find the tension in the rope if m140kgandm2=60kg. Also find the time after the time after which they will be at same horizontal level if they start from rest and are initially separted by 5 m.
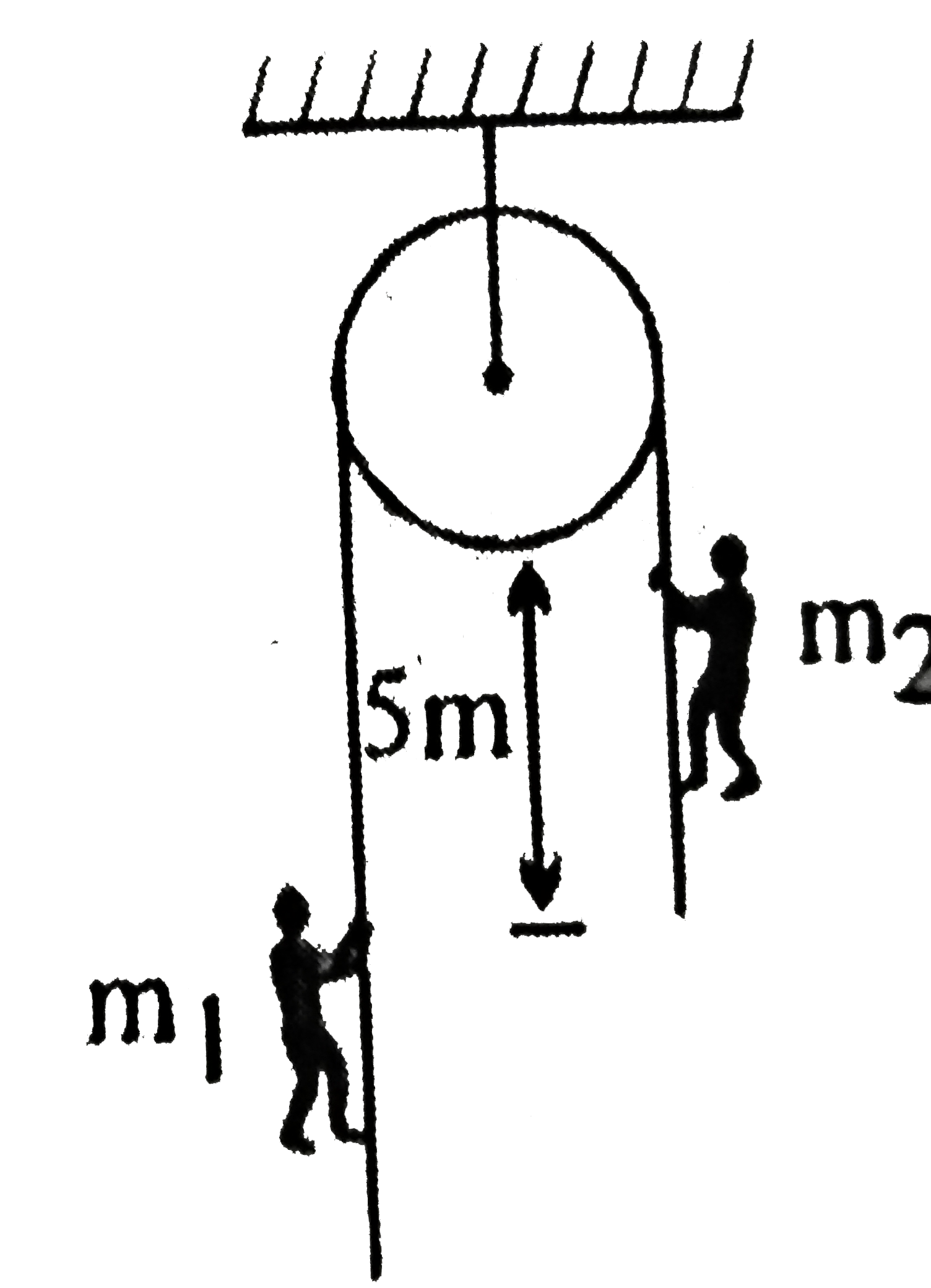
View SolutionA man of mass m is suspended in air by holding the rope of a ballon of mass M. As the man climbs up the rope, the ballon
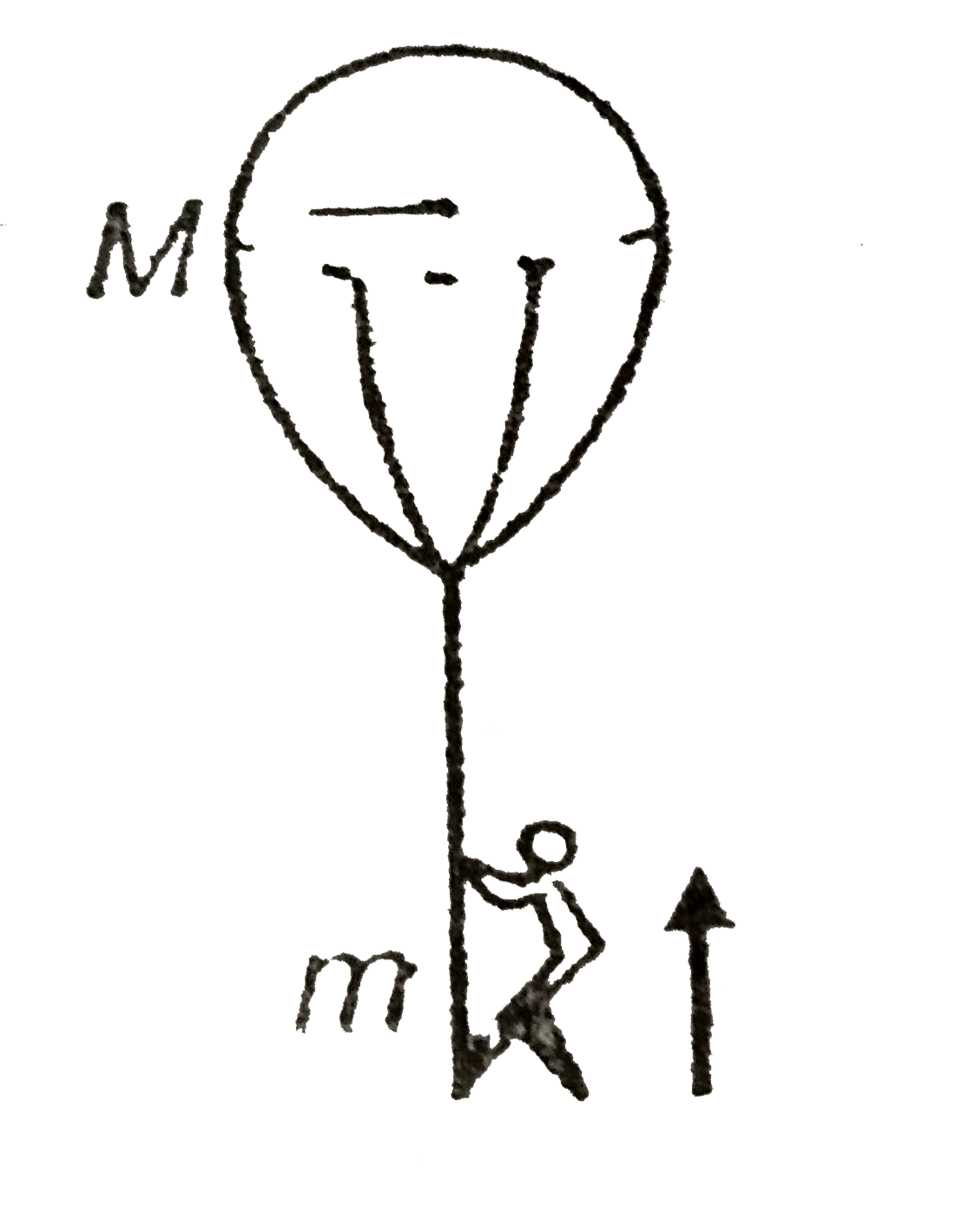
View SolutionA rope of mass 5 kg is hanging between two supports as shown. The tension at the lowest point of the rope is close to (take g = 10m/s2)

View Solution
