A radioactive nucleus initially at rest decays by emitting an electron and neutron at right angle to one another. The momentum of neutron is 3.2×10−24kgm/s and the momentum of neutron is 6.4×10−24kgm/sec . The direction of the recoiling nucleus with that of the electron motion is:
π−tan−1(2)
tan−1(2)
tan−1(0.5)
π2+tan−1(2)
The correct Answer is:A
Pe=3.2×10−23kgm/s , Pn=6.4×10−23kgm/s .
PR=√P2e+P2n=√(3.2)2+(6.4)2×10−23kgm/s .
tanθ=(PnPe=6.4×10−233.2×10−23=2 .
According to law of conservation of momentum, the residual nucleus must move in a direction just opposite to that of →PR , as shown in figure. hence, direction of the recoiling nucleus with that of the electron motion ϕ=π−θ=π−tan−1(2) . 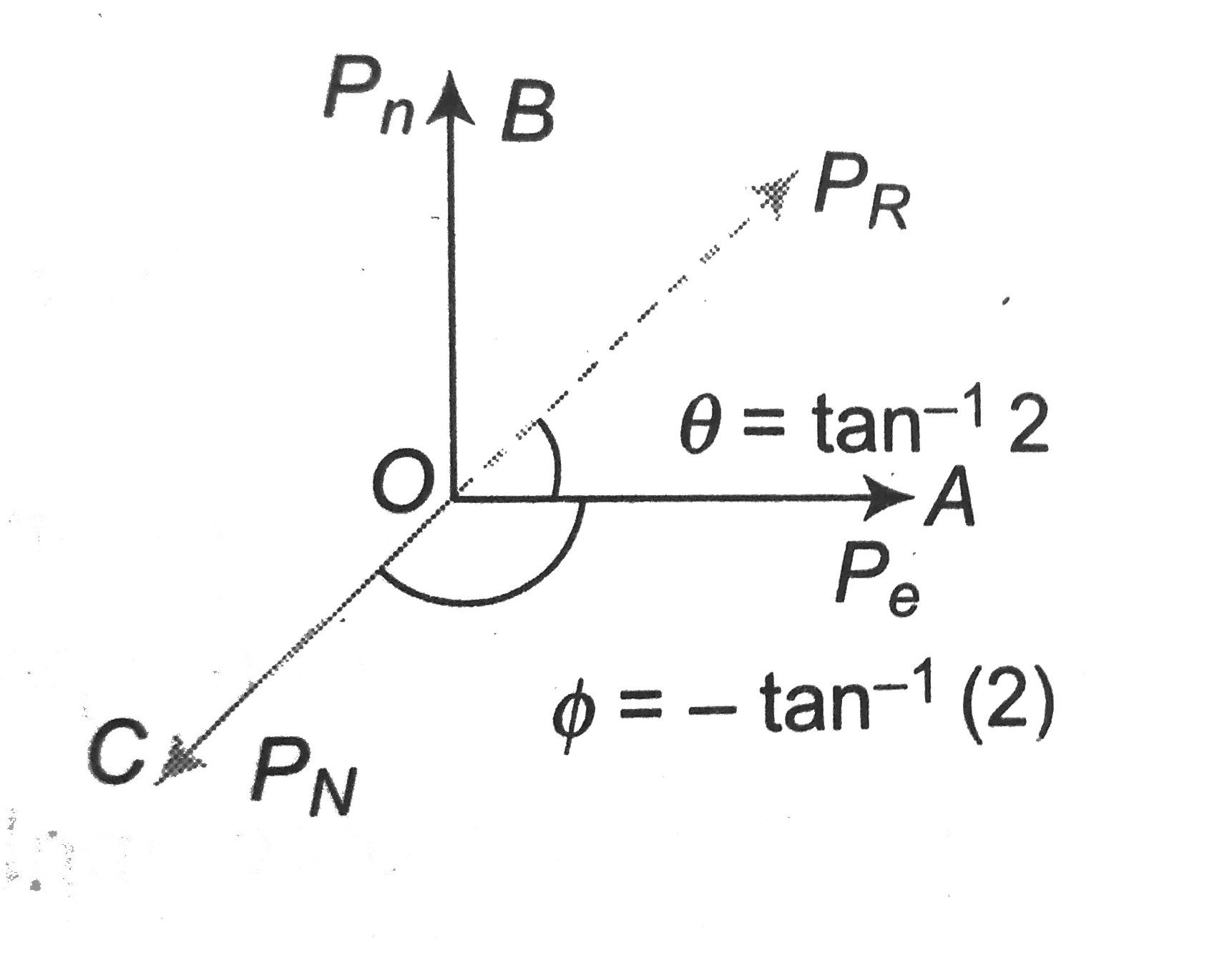
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Equilibrium Of A Particle
19 Videos
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Applications Of Newton'S Laws Of Motion
33 Videos
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test
30 Videos
- MOTION IN TWO DIMENSIONBOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Chapter Test
29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test
29 Videos
Similar Questions
A neutron initially at rest, decays into a proton, an electron and an antineutrino. The ejected electron has a momentum of 1.4×10−26 kg.m/s nd the antineutrino 6.4×1027 kgm/s. Find the recoil speed of the proton a. if the electron and the antineutrino are ejected along the same directioin and b. if they are ejected along perpendicular directions. Mass of the proton 1.67×10−27kg.
View SolutionA neutron intially at rest, decays into a proton, an electron and an antineutrio. The ejected electron has a momentum of p1=1.4×10−28 kg-m/s and the antineutrino p2=6.5×10–27 kg-m/s. Find the recoil speed of the proton
if the electron and the antineutrino are ejected along the the same direection.
View Solution
Knowledge Check
The linear momentum of the electron in the ground state of H-atom is 2×10−24kgm/s, its linear momentum in the 8th orbit is
A2.5×10−25kgm/sB5.2×10−25kgm/sC5.2×10−15kgm/sD2.5×10−15kgm/sThe uncertainty in momentum of an electron is 1×10−5kgm/s. The uncertainty in its position will be (h=6.62×10−34kgm2/s).
A1.05×10−28mB1.05×10−26mC5.27×10−30mD5.25×10−28mIf the mass of neutron = 1.7×10−27 kg, then the de-Broglie wavelength of neutron of energy 3 eV is (h=6.6×10−34Js)
A1.6×10−16mB1.6×10−11mC1.4×10−10mD1.4×10−11m
The de-broglie wavelength associated with photon changes by 0.25%. If its momentum is changed by 9×10−26kgms−1, find the initial momentum of electron.
View SolutionThe uncertainty in momentum of an electron is 1×10−5 kg mis. The uncertainty in its position will be (h=6.62×10−34kgm2/s)
View SolutionA neutron is confined to a nucleus of size 2×10−14m. The minimum momentum of the electron may be
View SolutionA radioactive nucleus (initial mass number A and atomic number Z) emits 3α-particles and 2 positrons. The ratio of number of neutrons to that of protons in the final nucleus will be
View SolutionThe position of both , an electron and a helium atom is known within 1.0 nm. Further the momentum of the electron is known within 5.0×10−26kgms−1 The minimum uncertainty in the measurement of the momentum of the helium atom is
View Solution
