A particle reaches its highest point when it has covered exactly one half of its horizontal range. The corresponding point on the displacement -time graph is charecterized by :
negative slope and zero curvature
zero slope and negative curvature
zero slope and positive curvature
positive slope and zero curvature
The correct Answer is:c
To solve the problem, we need to analyze the motion of a particle projected at an angle and determine the characteristics of the displacement-time graph when the particle reaches its highest point after covering half of its horizontal range.
1. Understanding Projectile Motion:
- When a particle is projected at an angle θ, it follows a parabolic trajectory due to the influence of gravity. The horizontal range (R) is the total horizontal distance covered when the particle returns to the same vertical level from which it was projected.
2. Identifying the Highest Point:
- The highest point of the projectile's path is reached when the vertical component of its velocity becomes zero. At this point, the particle has covered half of its horizontal range (R/2).
3. Analyzing the Displacement-Time Graph:
- The displacement in the vertical direction (y) will be at its maximum at the highest point, while the horizontal displacement (x) will be at R/2.
- On a displacement-time graph, the y-axis represents displacement and the x-axis represents time.
4. Slope of the Displacement-Time Graph:
- The slope of the displacement-time graph at any point represents the velocity of the particle at that time.
- At the highest point, the vertical velocity is zero (the particle is momentarily at rest in the vertical direction), which means the slope of the graph (dy/dt) at this point is zero.
5. Curvature of the Displacement-Time Graph:
- The curvature of the graph indicates how the slope is changing.
- Since the particle is transitioning from moving upwards to moving downwards, the graph will have a positive curvature at the highest point. This is because the graph will be concave upwards at this point.
6. Conclusion:
- Therefore, at the highest point where the particle has covered half of its horizontal range, the displacement-time graph is characterized by:
- A slope of zero (indicating zero vertical velocity).
- Positive curvature (indicating the transition from increasing to decreasing displacement).
Final Answer:
The corresponding point on the displacement-time graph is characterized by a slope of zero and positive curvature.
- When a particle is projected at an angle θ, it follows a parabolic trajectory due to the influence of gravity. The horizontal range (R) is the total horizontal distance covered when the particle returns to the same vertical level from which it was projected.
- The highest point of the projectile's path is reached when the vertical component of its velocity becomes zero. At this point, the particle has covered half of its horizontal range (R/2).
- The displacement in the vertical direction (y) will be at its maximum at the highest point, while the horizontal displacement (x) will be at R/2.
- On a displacement-time graph, the y-axis represents displacement and the x-axis represents time.
- The slope of the displacement-time graph at any point represents the velocity of the particle at that time.
- At the highest point, the vertical velocity is zero (the particle is momentarily at rest in the vertical direction), which means the slope of the graph (dy/dt) at this point is zero.
- The curvature of the graph indicates how the slope is changing.
- Since the particle is transitioning from moving upwards to moving downwards, the graph will have a positive curvature at the highest point. This is because the graph will be concave upwards at this point.
- Therefore, at the highest point where the particle has covered half of its horizontal range, the displacement-time graph is characterized by:
- A slope of zero (indicating zero vertical velocity).
- Positive curvature (indicating the transition from increasing to decreasing displacement).
The corresponding point on the displacement-time graph is characterized by a slope of zero and positive curvature.
Topper's Solved these Questions
- MOTION IN TWO DIMENSIONBOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Projectile From A Height And Movingframe
19 Videos
- MOTION IN TWO DIMENSIONBOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Projection From Inclined Plane
20 Videos
- MOCK TESTBOOK - A2ZCHAPTER - MOCK TESTEXERCISE - Motion With Constant Acceleration
15 Videos
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test
30 Videos
Similar Questions
Knowledge Check
A particle is projected from the ground with an initial speed of v at an angle θ with horizontal. The average velocity of the particle between its point of projection and highest point of trajectroy is :
Av2√1+2cos2θBv2√1+2cos2θCv2√1+3cos2θDvcosθA particle is projected with speed u at angle θ to the horizontal. Find the radius of curvature at highest point of its trajectory
Au2cos2θ2gB√3u2cos2θ2gCu2cos2θgD√3u2cos2θgA particle of mass m is projected with a velocity μ at an angle of θ with horizontal.The angular momentum of the particle about the highest point of its trajectory is equal to :
Amu3sin2θcosθ3gB3mu3sin2θcosθ3gCmu3sin2θcosθ2gD2mu3sinθcos2θ3g
A particle is projected from the ground with an initial speed v at an angle θ with horizontal. The average velocity of the particle between its point of projection and highest point of trajectory is [EAM2013]
View SolutionA particle is projected from the ground with an initial speed of 5ms−1 at an angle of projection 60° with horizontal. The average velocity of the particle between its time of projection and the time it reaches highest point of trajectory
View SolutionA particle thrown up vertically reaches its highest point in time t1 and returns to the ground in a further time t2. The air resistance exerts a constant force on the particle opposite to its direction of motion.
View SolutionA particle of mass m is projected at an angle α to the horizontal with an initial velocity u. The work done by gravity during the time it reaches its highest point is
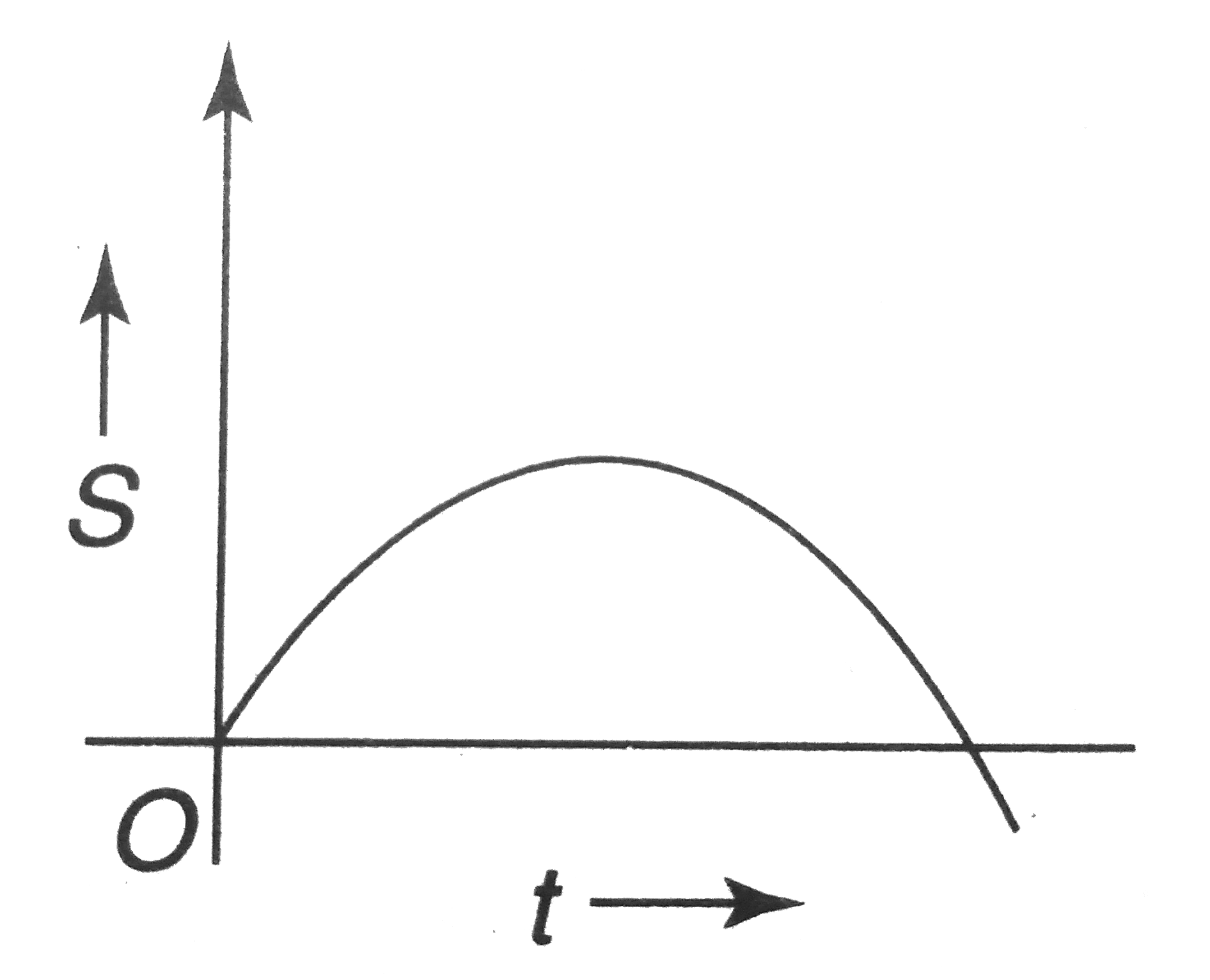
View SolutionThe graph of displacement versus time is shown. Its corresponding velocity-time graph will be.
View Solution