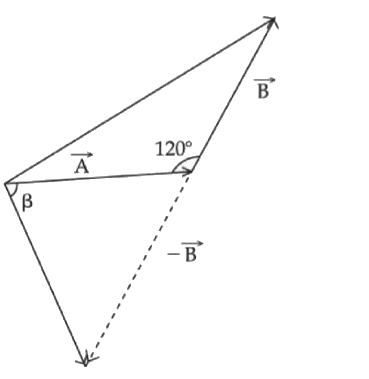
Vectors $\to A$ and $\to B$ include an angle $θ$ between them. If $(\to A + \to B)$ and $(\to A - \to B)$ respectively subtend angles $α and β$ with $\to A$ , then $(tan α + tan β)$ is

A

$\frac{(A B sin θ)}{(A^{2} + B^{2} {cos}^{2} θ)}$

B

$\frac{(2 A B sin θ)}{(A^{2} - B^{2} {cos}^{2} θ)}$

C

$\frac{(A^{2} {sin}^{2} θ)}{(A^{2} + B^{2} {cos}^{2} θ)}$

D

$\frac{(B^{2} {sin}^{2} θ)}{(A^{2} - B^{2} {cos}^{2} θ)}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$tan α = \frac{B sin θ}{A + B cos θ}$ ….(i)
Similarly, $tan β \frac{B sin θ}{A - B cos θ}$ ....(ii)
Where $β$ is the angle made by the vector $(\to A + \to B)$ with $\to A$ .
Note that the angle between $\to A$ . and $- - \to - B$ is $(180^{\circ} - θ)$ . Adding (i) and (ii), we get
$tan α + tan β = \frac{B sin θ}{A + B cos θ} + \frac{B sin θ}{A - B cos θ}$
$(A B sin θ - B^{2} sin θ cos θ)$
$= \frac{+ A B sin θ + B^{2} sin θ cos θ}{(A + B cos θ) (A - B cos θ)}$
$\frac{2 A B sin θ}{(A^{2} - B^{2} {cos}^{2} θ)}$

|

Updated on:21/07/2023

Class 11 PHYSICS VECTOR

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Vectors vecà and vecb include an angle $θ$ between them. If $(\to a + \to b)$ and $(\to a - \to b)$ respectively subtend angles $α and β$ with $\to a$ , then $(tan α + tan β)$ is
A $\frac{(ab sin θ)}{(a^{2} + b^{2} {cos}^{2} θ)}$
B $\frac{2 ab sin θ}{(a^{2} - b^{2} {cos}^{2} θ)}$
C $\frac{a^{2} {sin}^{2} θ}{(a^{2} + b^{2} {cos}^{2} θ)}$
D $\frac{(b^{2} {sin}^{2} θ)}{(a^{2} - b^{2} {cos}^{2} θ)}$
Question 2 - Select One
The angle between vectors $(\to A \times \to B) and (\to B \times \to A)$ is :
A $π$ rad
B $\frac{π}{2}$ rad
C $\frac{π}{4}$ rad
Dzero
Question 3 - Select One
If the resultant of $\to A$ and $\to B$ makes angle $α$ with $\to A$ and $β$ with $\to B$ , then
A $α < β$ always
B $α < β$ if $A < B$
C $α < β$ if $A > B$
D $α < β$ if A=B

A2Z-VECTORS-Problems Based On Mixed Concepts

Home
Ask Doubt
Profile