Two blocks of masses m1 and m2 are connected by a string of negligible mass which pass over a frictionless pulley fixed on the top of an inclined plane as shown in figure. The coefficient of friction between m1 and plane is μ.
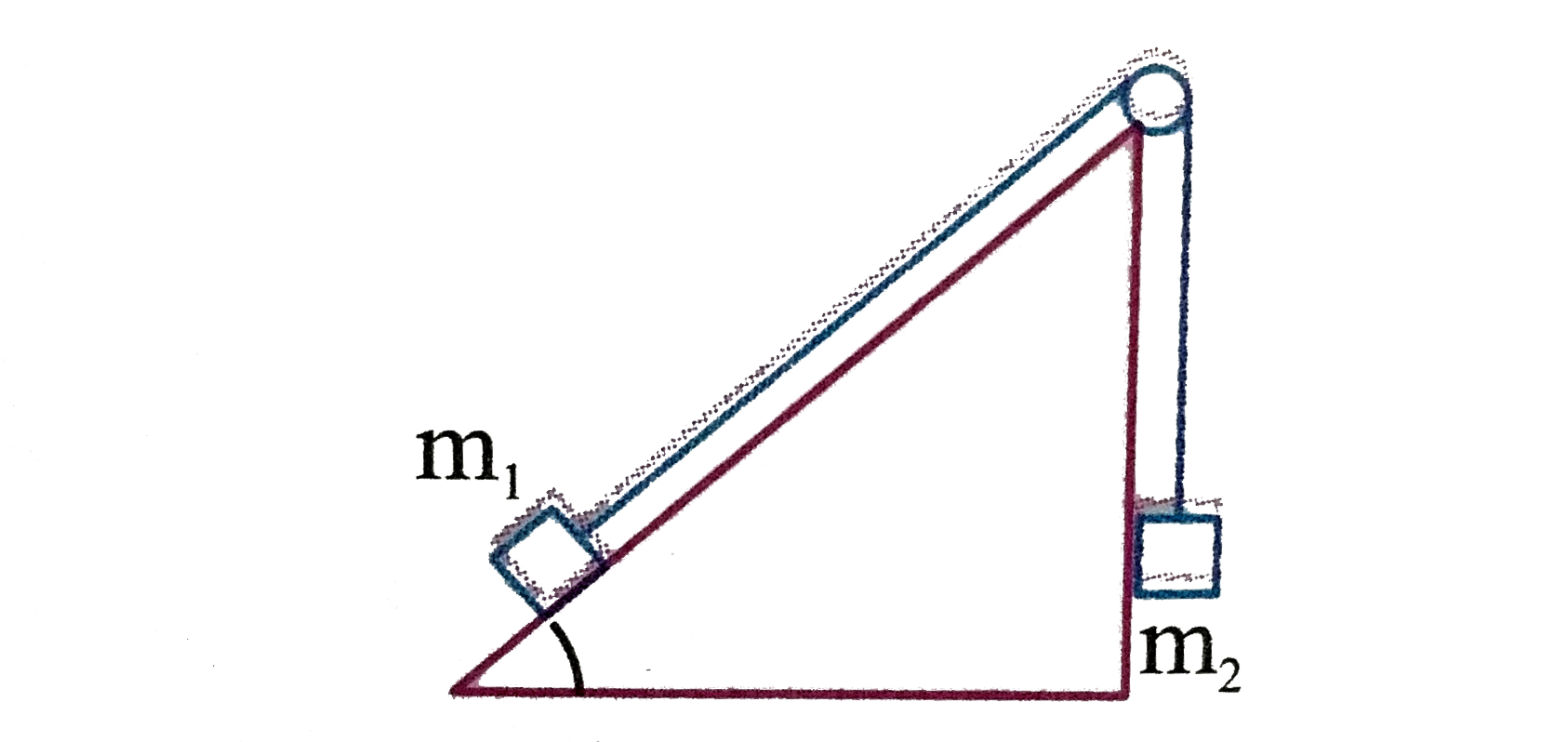
If m1=m2 the mass m1 first begin to move up inclined plane when the agle of inclination is θ,then μ=tanθ.
If m1=m2 the mass m1 first begin to move up the inclined plane when the angle of inclination is θ, then mu=sectheta-tantheta.
If m1=2m2 the mass m1 first begin to slide down the plane if μ=2tanθ.
If m1=2m2 the mass m1 first begin to slide down the plane if μ=tanθ−12secθ.
The correct Answer is:B, D
(b) The blocks m1 will just begin to move up the plane if the downward force m2g due to mass m2 trying to pull the mass m1 up the plane just equals the force
m2g=(m1gsinθ+μm1gcosθ)
mg=mgsinθ+μcosθ
mg(1−sinθ)=μmgcosθ
μ=secθ−tanθ
So, choice (b) is correct
(d) The block m1 will just begin to move down the plane, if the downward force (m1gsinθ−μm1gcosθ) on m1 just equals the upward force m2 of acting on m1 due to m2 if
m2g=m1g(sinθ−μcosθ)
m2g=2m2g(sinθ−μcosθ)
12=sinθ−μcosθ
12cosθ=tanθ−μ
μ=tanθ−12secθ
Similar Questions
Two blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
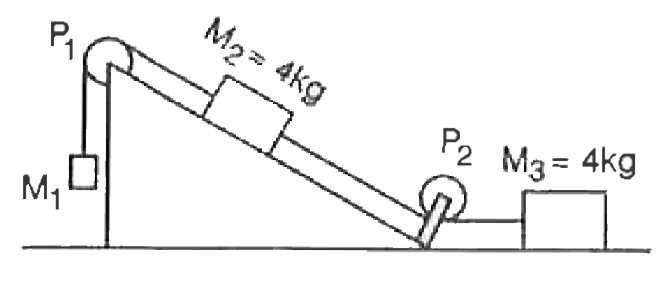
View SolutionMasses M1,M2andM3 are connected by string of negligible mass which pass over massless and frictionless pulleys P1andP2 as shown in figure 7.15. The masses move such that the string between P1andP2 is parallel to the incline and the portion of the string between P2andM3 is horizontal. The masses M2andM3 are 4.0 kg each and the coefficient of kinetic friction between the masses and the surfces is 0.25. The inclined plane makes an angle of 37∘ with the horizontal. If the mass M1moves downwards with a uniform velocity, find (i) the mass of M1, (ii) the tension in the horizontal portion. (g=9.8ms−2,sin37∘=35)
View Solution
Knowledge Check
Two blocks of masses M1=4 kg and M2=6kg are connected by a string of negligible mass passing over a frictionless pulley as shown in the figure below. The coefficient of friction between the block M1 and the horizontal surface is 0.4. when the system is released, the masses M1 and M2 start accelrating. What additional mass m should be placed over M1 so that the masses (M1+m) slide with a uniform speed?
 A12 kgB11 kgC10 kgDkg
A12 kgB11 kgC10 kgDkgTwo block of masses M1 and, M2 are connected with a string which passed over a smooth pulley . The mass M1 is placed on a tough inclined plane as shown in figure .The coefficient of friction between and block and the inclined plane is μ what should be the minimum mass M2 so that the block M1 slides upwards?
 AM2=M1(sinθ+μcosθ)BM2=M1(sinθ−μcosθ)CM2=M1sinθ+μcosθDM2=M1sinθ−μcosθ
AM2=M1(sinθ+μcosθ)BM2=M1(sinθ−μcosθ)CM2=M1sinθ+μcosθDM2=M1sinθ−μcosθTwo blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2

Two blocks of mass M and 3M (in kg) are connected by an inextensible light thread which passes over a light frictionless pulley. The whole system is placed over a fixed horizontal table as shown.The coefficient of friction between the blocks and table surface is μ. The pulley is pulled by a string sttached to its centre and accelerated to left with acceleration a(ms2). Assume that gravity acts with constant acceleration g(ms2) downwards through the plane of table. Then:
(a) Find the forizontal accelration of both the blocks (Assume that both the blocks are moving.)
(b) What is the maximum acceleration a, for which the block of mass 3 M will remain stationary?
View SolutionMasses M1,M2andM3 are connected by string of negligible mass which pass over massless and frictionless pulleys P1andP2 as shown in figure 7.15. The masses move such that the string between P1andP2 is parallel to the incline and the portion of the string between P2andM3 is horizontal. The masses M2andM3 are 4.0 kg each and the coefficient of kinetic friction between the masses and the surfces is 0.25. The inclined plane makes an angle of 37∘ with the horizontal. If the mass M1moves downwards with a uniform velocity, find (i) the mass of M1, (ii) the tension in the horizontal portion. (g=9.8ms−2,sin37∘=35)

View SolutionTwo blocks of mass m1 and m2(m2>m1) are placed in contact with each other on an inclined plane as shown in figure . The coefficient of friction between m1 and surface is μ1 and between m2 and surface is μ2.



View SolutionTwo blocks of masses m1=1kgandm2=2kg are connected by a string and side down a plane inclined at an angle θ=45∘ with the horizontal. The coefficient of sliding friction between m1 and plane is μ1=0.4, and that between m2 and plane is μ2=0.2. Calculate the common acceleration of the two blocks and the tension in the string.

View Solution
Two blocks of masses m1 and m2 connected by a string are placed gently over a fixed inclined plane, such that the tension in the connecting string is initially zero. The coefficient of friction between m1 and inclined plane is μ1, between μ2 and the inclined plane is μ2. The tension in the string shall continue to remain zero if
View Solution
