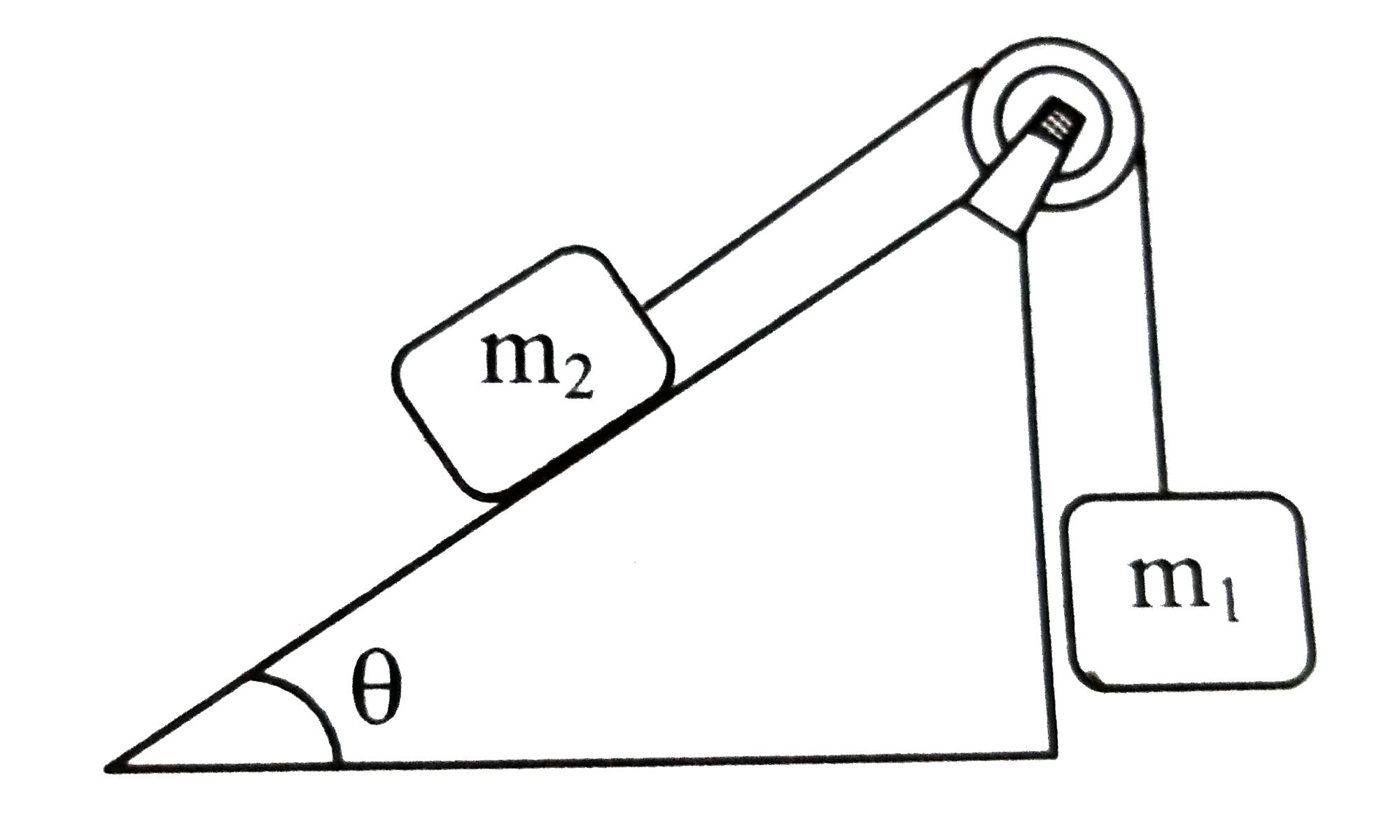
Two blocks of masses m1 and m2 connected by a string are placed gently over a fixed inclined plane, such that the tension in the connecting string is initially zero. The coefficient of friction between m1 and inclined plane is μ1, between μ2 and the inclined plane is μ2. The tension in the string shall continue to remain zero if
μ1>tanα and μ2tanβ
μ1<tanα and μ2>tanβ
μ1>tanα and μ2tanβ
μ2>tanα and μ2>tanβ
The correct Answer is:C
The tension in the string initially is zero. If μ1>tanα and μ2>tanβ, both the blocks will not move down the incline and the tension in the string shall countinue to remain zero.
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICSCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Fill in the blanks type
26 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICSCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Comprehension Type
31 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICSCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Multiple Correct Answer Type
54 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICSCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
- CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONEXERCISE - Question Bank
38 Videos
Similar Questions
Knowledge Check
Two blocks of masses m1 and m2 are connected by a string of negligible mass which pass over a frictionless pulley fixed on the top of an inclined plane as shown in figure. The coefficient of friction between m1 and plane is μ.
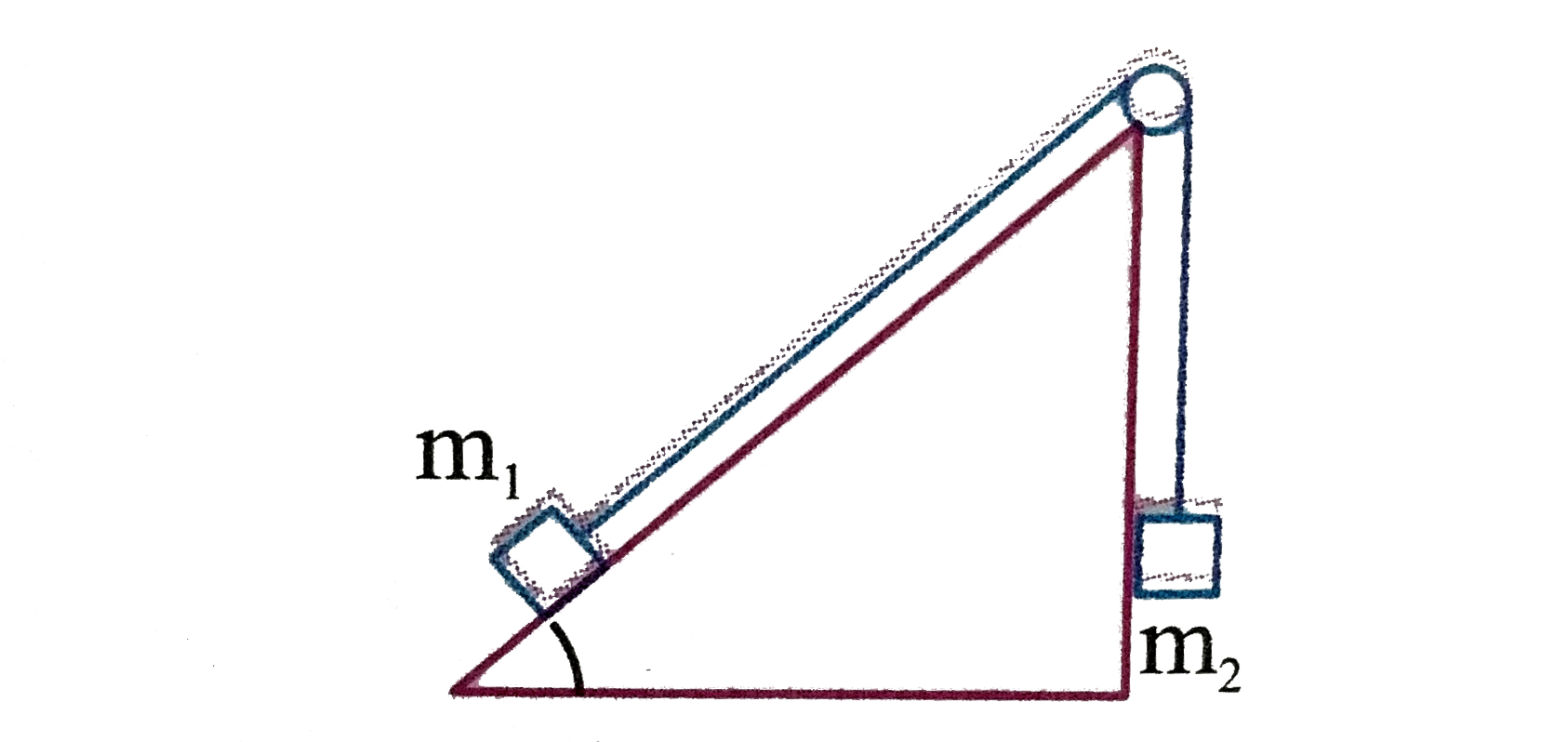 AIf m1=m2, the mass m1 first begin to move up inclined plane when the angle of inclination θ, then μ=secθ−tanθBIf m1=m2, then mass m1 first begin to side down the plane if μ=secθ−tanθ.CIf m1=2m2, then mass m1 first begins to slide down the plane if μ=2tanθ.DIf m1=2m2, then mass m1 first begins to slide down the plane if μ=tanθ−12secθ.
AIf m1=m2, the mass m1 first begin to move up inclined plane when the angle of inclination θ, then μ=secθ−tanθBIf m1=m2, then mass m1 first begin to side down the plane if μ=secθ−tanθ.CIf m1=2m2, then mass m1 first begins to slide down the plane if μ=2tanθ.DIf m1=2m2, then mass m1 first begins to slide down the plane if μ=tanθ−12secθ.Two blocks are kept on an inclined plane and tied to each other with a mass-less string. Coefficient of friction between m1 and inclined plane is μ1 & that betweeb m2 & the inclined is μ2. Then :
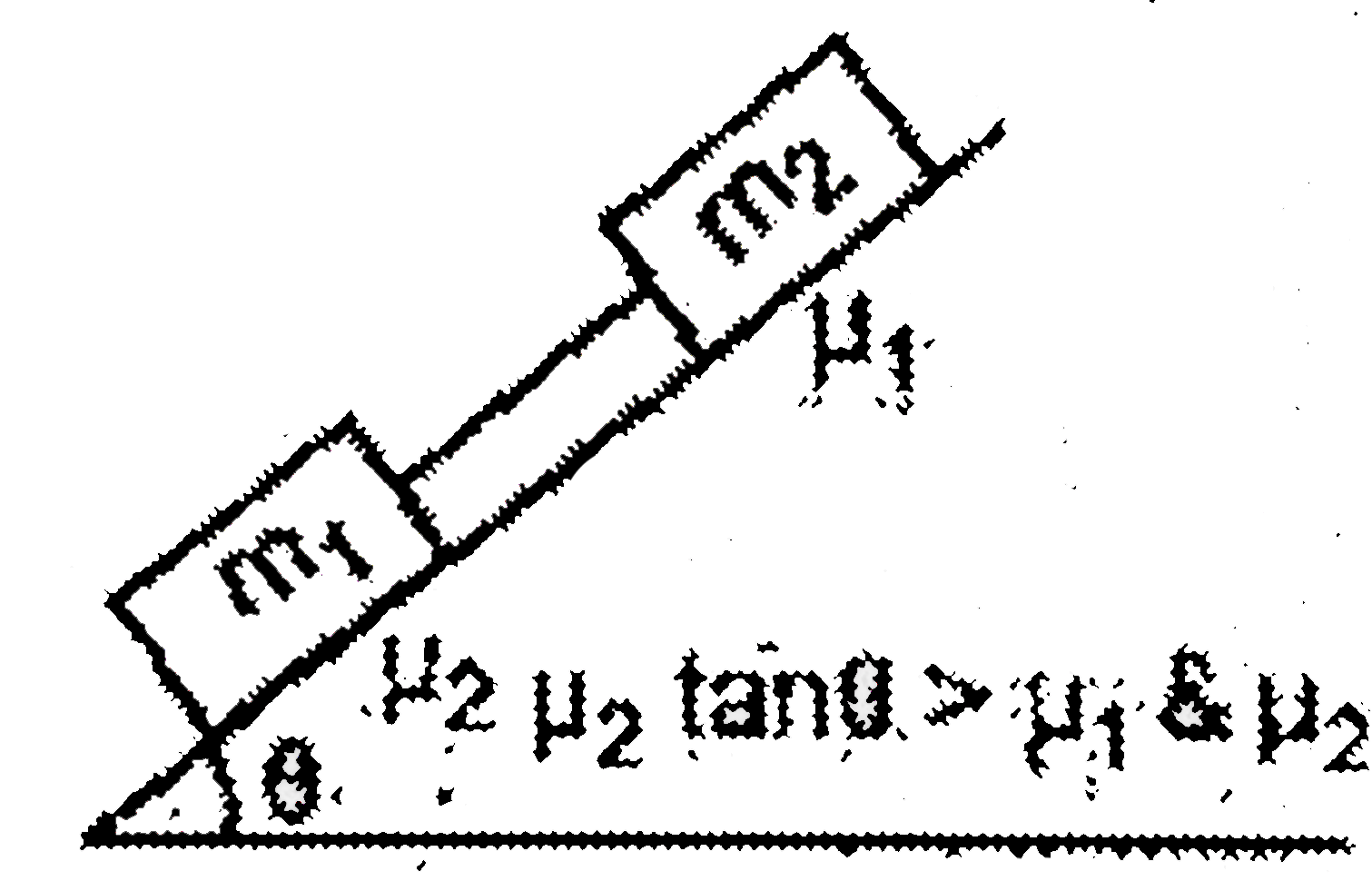 AThe tension in the string in zero if μ1>μ2BThe tension in the string is zero if μ1<μ2CTension in the string is always zero irrespective of μ1&μ2DNone of these
AThe tension in the string in zero if μ1>μ2BThe tension in the string is zero if μ1<μ2CTension in the string is always zero irrespective of μ1&μ2DNone of theseA block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
Two blocks of masses m1=1kgandm2=2kg are connected by a string and side down a plane inclined at an angle θ=45∘ with the horizontal. The coefficient of sliding friction between m1 and plane is μ1=0.4, and that between m2 and plane is μ2=0.2. Calculate the common acceleration of the two blocks and the tension in the string.

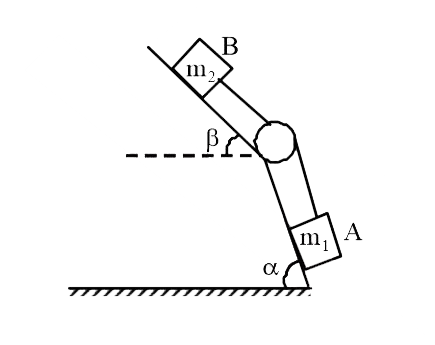
View SolutionTwo blocks A and B of masses m1 and m, are connected by an inextensible string rest on two smooth planes inclined at angle α and β as shown. The tension in string is -
View SolutionTwo blocks of masses m1andm2 are kept touching each other on a rough fixed inclined plane of inclination α. Coefficients of kinetic friction between the inclined plane and the block m1 is k1 and between the inclined plane and block m2 is k2. Find the force of interaction between the blocks in the process of motion.
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is .
View Solution