If the coefficient of friction between A and B is μ, the maximum acceleration of the wedge A for which B will remain at rest with respect to the wedge is

μg
g(1+μ1−μ)
gμ
g(1−μ1+μ)
The correct Answer is:B, C, D

FBD of block B w.r.t. wedge A, for maximum a:
Perpendicular to wedge:
∑fy=(mgcostheta+masintheta-N)=0<br>andsumf_x^=mgsinθ+μN−macosθ=0 (for maximum a)
⇒mgsinθ+μ(mgcosθ+masinθ)−mcosθ=0
⇒a(gsinθ+μgcosθ)cosθ−μsinθ
For θ=45∘
a=(tan45∘+μcot45∘−μ),a=g(1+μ1−μ)
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICSCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Fill in the blanks type
26 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICSCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Comprehension Type
31 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICSCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Multiple Correct Answer Type
54 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICSCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
- CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONEXERCISE - Question Bank
38 Videos
Similar Questions
If the coefficient of friction between the wedge A and block B shown in the figure is μ, then the maximum possible horizontal acceleration of A for which B doesn’t slip is [ angle of inclination of wedge = 45∘ ]

View SolutionThe coefficient of friction between the block and the wedge is μ. Friction between the wedge and the table is to be neglected.
View Solution
Knowledge Check
The minimum value of acceleration of wedge for which the block start sliding on the wedge, is:
Ag(cosθ+μsinθsinθ−μcosθ)Bg(sinθ+μcosθcosθ−μsinθ)Cg(sinθ−μcosθsinθ+μcosθ)Dg(cosθ−μsinθsinθ+μcosθ)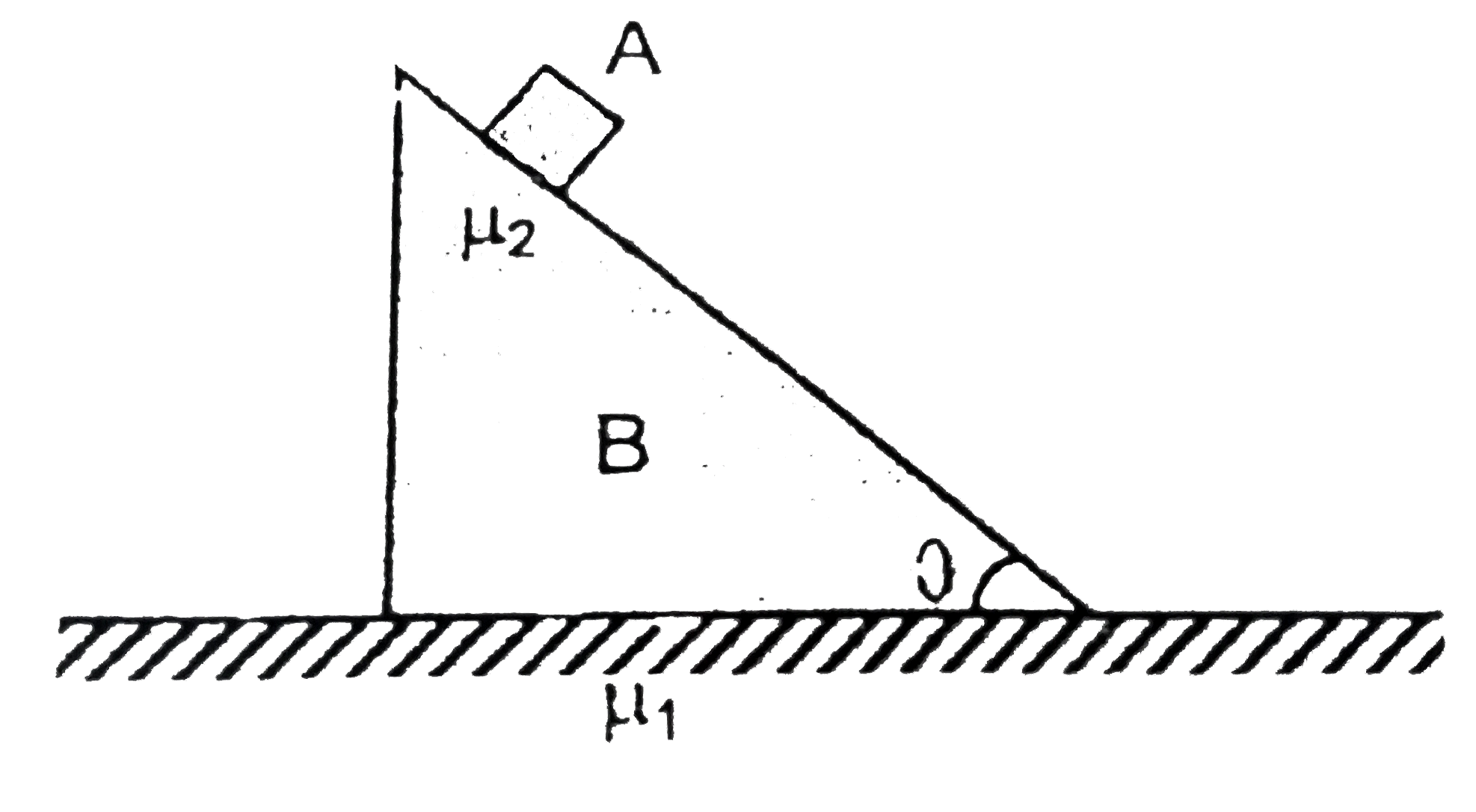
A wedge B of mass 2 m is placed on a rough horizontal suface. The coefficient of friction between wedge and the horizontal surface is μ1. A block of mass m is placed on wedge as shown in the figure. The coefficient of friction between block and wedge is μ2. The block and wedge are released from rest.
Q. Suppose the inclined surface of the wedge is at θ=37∘ from angle from horizontal and μ2=0 are wedge will remain in equilibrium ifAμ1=0.1Bμ1=0.2Cμ1=0.3Dμ1=0.4Figure shows an irregular wedge of mass m placed on a smooth horizontal surface. Part BC is rough.
If the coefficient of friction between the block and wedge is μ, and the block comes to rest with respect to wedge at a point E on the rough surface then BE will beAHμBH−hμChμDnone of these
The coefficient of friction between the wedge and the table is μ, the friction between the rod and the wedge being negligible.
View SolutionThe coefficient of friction between the wedge and the table is μ. Friction between the block and the wedge is to be neglected.
View SolutionA block lies on a wedge with the slope angle α. The coefficient of static friction between the bar and the wedge is μ<tanα. What should be the acceleration of the wedge to prevent the bar from sliding down?
View SolutionWedge is fixed on horizontal surface. Block A is pulled upward by applying a force F as shown in figure and there is no friction between the wedge and the block A while coefficient of friction between A and B is μ. If there is no relative motion between the block A and B then frictional force developed between A and B is
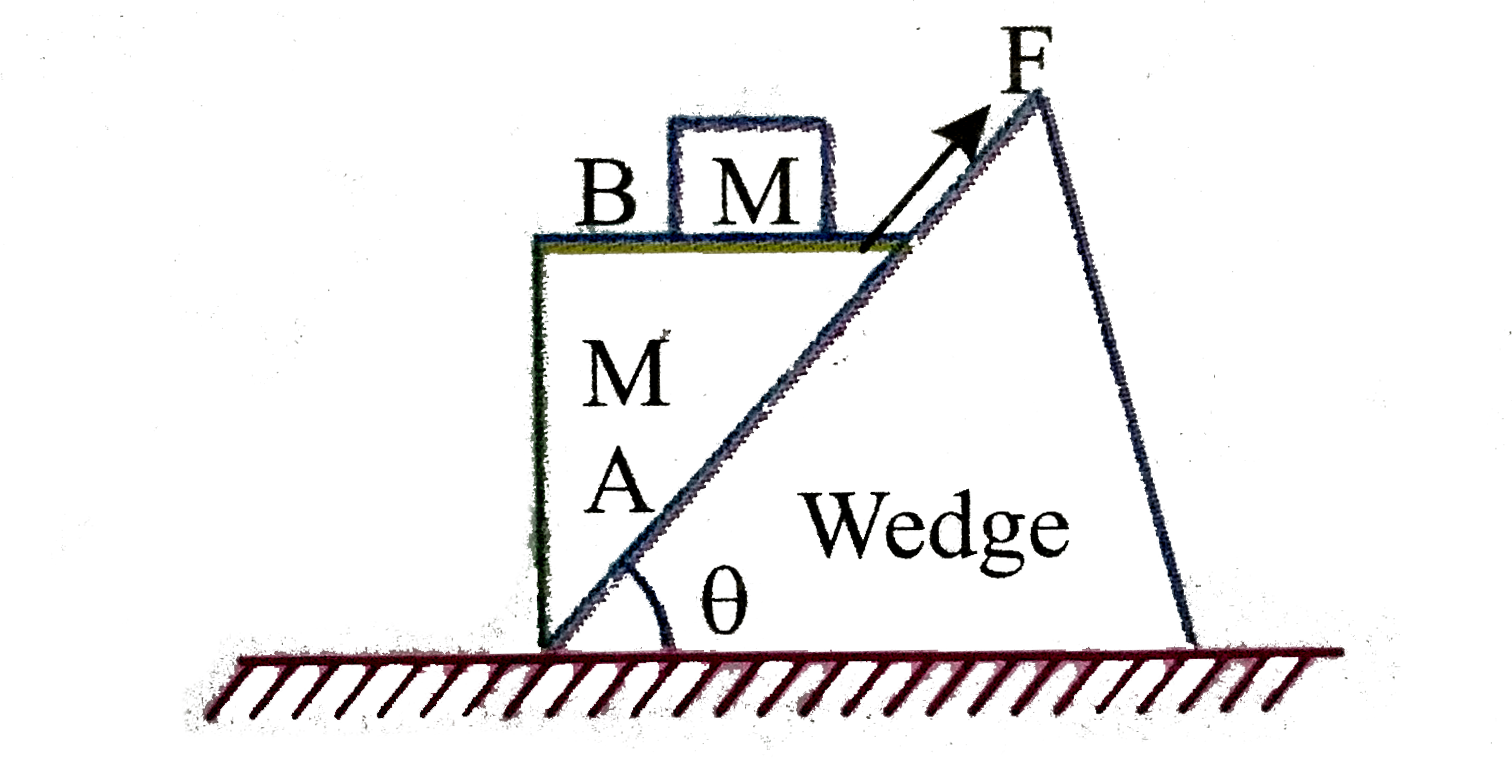
View SolutionA block of mass 2 kg is kept on a smooth wedge of mass 3 kg and wedge is kept on a rough horizontal surface. A vertical force of 60 N is applied on the minimum coefficient of friction between the wedge and horizontal surface, so that wedge remains at rest during the motion of block on the wedge ?
View Solution
