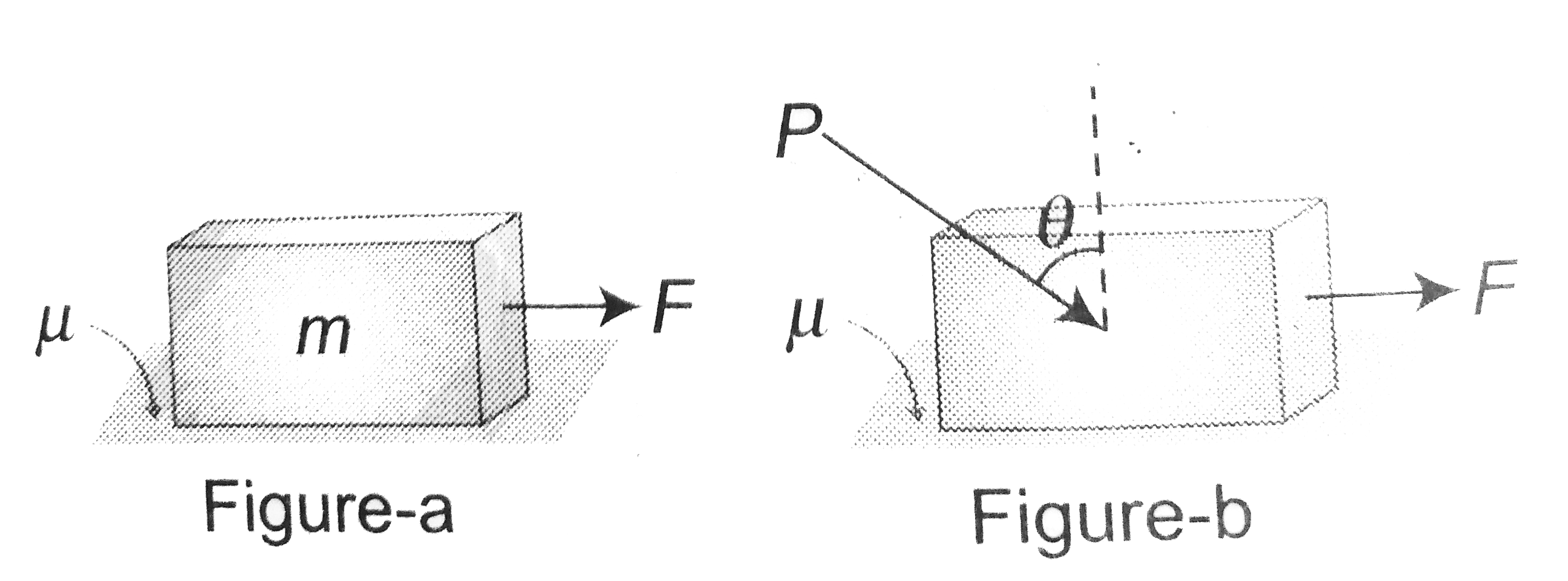
The coefficient of friction between the block and the horizontal surface is mu. The block moves toward right under action of horizontal force F (figure-a). Sometime later another force P is applied to the block making an angle theta (such that tanθ=μ) with vertical as shown in (figure-b). After application of force P , the acceleration of block shall.
increase
decrease
remain same
information insufficient to draw inference
The correct Answer is:C

The free body diagram of block in fig. b is as shown.
N=mg+Pcosθ
and acceleration of block
a=F+Psinθ−μ(mg+Pcosθ)m
a=F+Psinθ−sinθcosθ(mg+Pcosθ)m=F−μmgm
Hence P does not change acceleration.
Similar Questions
The coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View SolutionThe friction coefficient between the blocks is μ. If force F is applied on the lower block , analyse motion of two blocks.

View Solution
Knowledge Check
In Fig. 7.149 , coefficient of friction between the block and the floor is μ . Force F that will move the block on the floor with a uniform speed is :
 A(μsinθ+cosθ)mgB(μsinθ−cosθ) mgCμmgcosθ−μsinθDμmgsinθ−μcosθ
A(μsinθ+cosθ)mgB(μsinθ−cosθ) mgCμmgcosθ−μsinθDμmgsinθ−μcosθIn the arrangement shown in figure, coefficient of friction between the two blocks is μ=1/2. The force of friction acting between
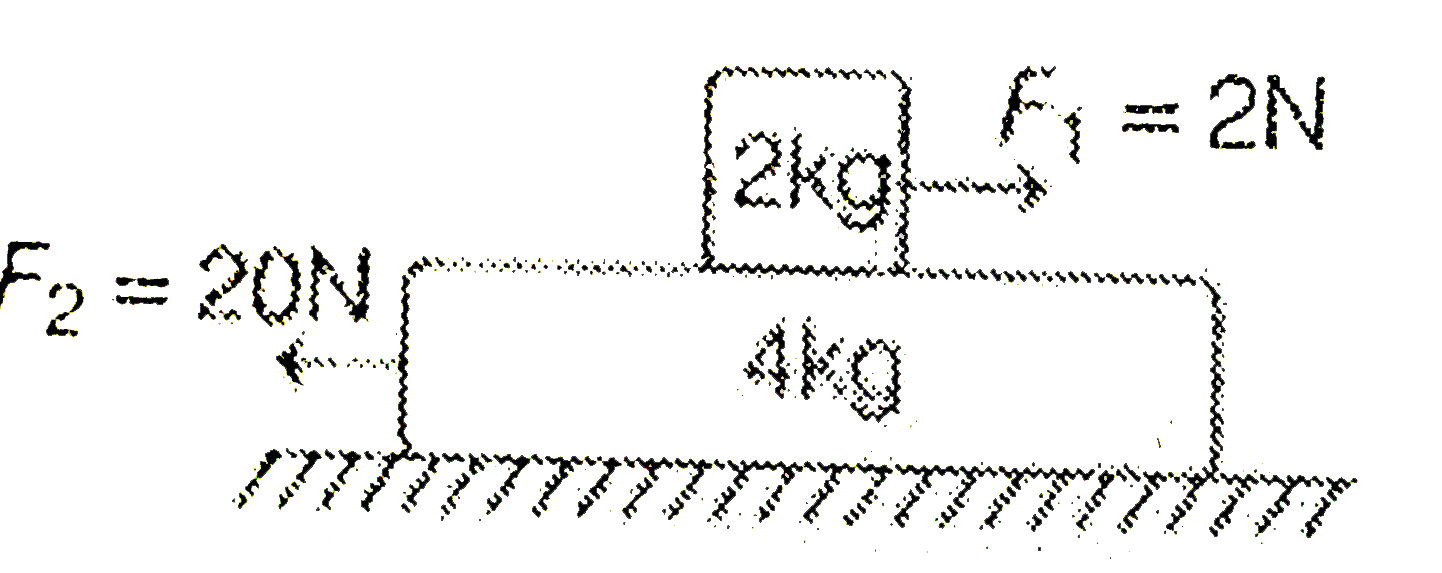 A8NB10NC6ND4N
A8NB10NC6ND4NA block of mass m is lying on horizontal surface of coefficient of friction μ. A force is applied to the block at an angle θ with the horizontal. The block will move with a minimum force F if
Aμ=tanθBμ=cosθCμ=sinθDμ=cotθ
A block of mass M is kept on as rough horizontal surface. The coefficient of static frictionbetween the block and the surface is μ. The block is to be pulled by applying a force to it. What minimum force is needed to slide the block? In which direction should this force act?
View SolutionThe coefficient of static friction between a block of mass m and an incline is μs=03, a. What can be the maximum angle θ of the incline with the horizontal so that the block does not slip on the plane? b. If the incline makes an angle θ2 with the horizontal, find the frictional force on the block.
View SolutionIn the situration shown in the figure the friction coefficient between M and the horizontal surface is μ. The force F is applied at an angle θ with vertical. The correct statements are
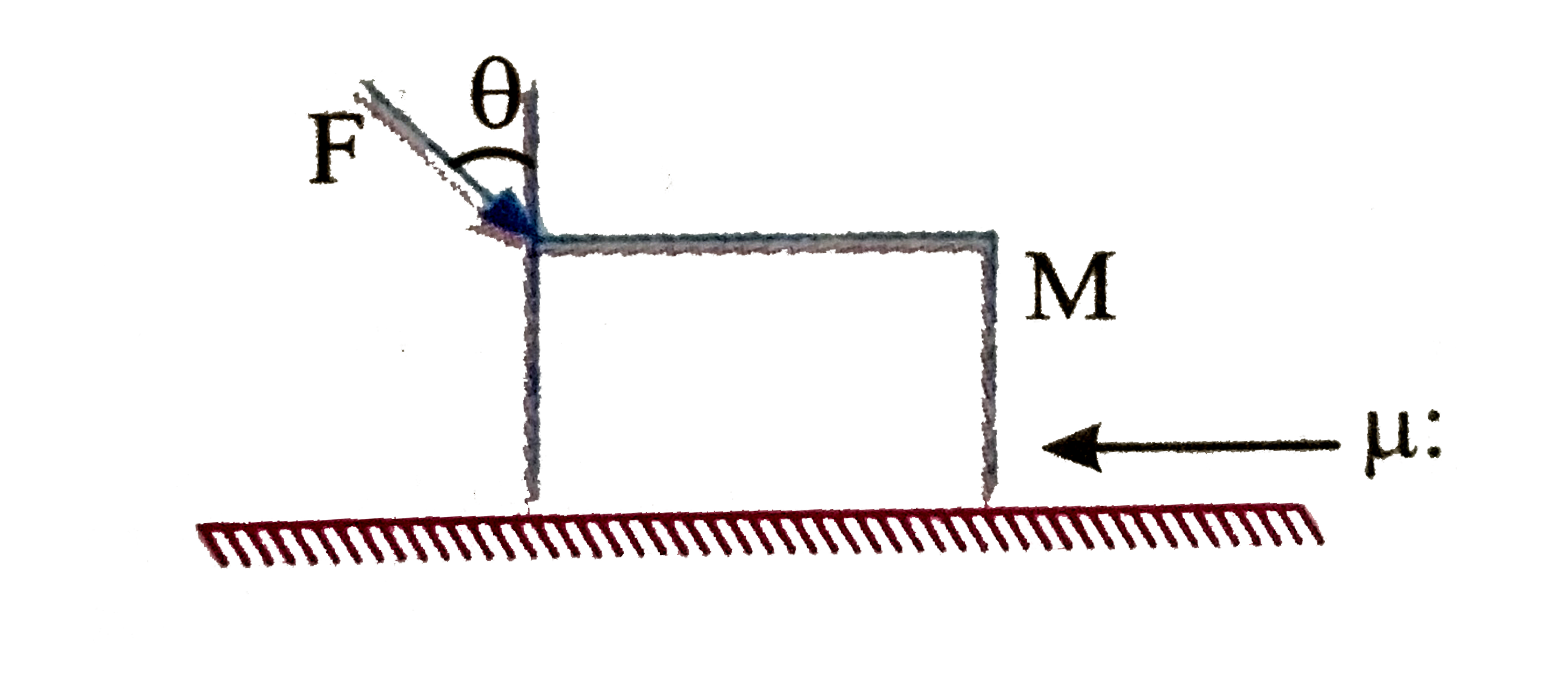
View SolutionIn the situatiobn shown in the figure the friction coefficient between M and the horizontal surface is μ. The force F is applied at an angle θ with vertical. The correct statements are :

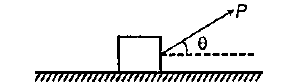
View SolutionA block of weight w rests on a horizontal plane. A force P inclined at an angle theta to the plane is applied to the block until it is on the of motion. Find the value of coefficient of friction.
View Solution