A particle is projected from a point (0,1) of Y-axis (assume + Y direction vertically upwards) aiming towards a point (4,9). It fell on ground along x axis in 1 sec. Taking g=10ms2 and all coordinate in metres. Find the X-coordinate where it fell.
(3,0)
(4,0)
(2,0)
(2√5,0)
The correct Answer is:C

tanθ=9−14−0=2
Now, −1=usinθ(1)−12g(1)2
usinθ=4 and θ=2√5⇒u=2√5
now,x=ucostheta(1)=(2sqrt5)xx(1)/(sqrt5)=2m
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICSChapter:CENGAGE PHYSICS DPPExercise:Fill in the blanks type
Explore 26 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICSChapter:CENGAGE PHYSICS DPPExercise:Comprehension Type
Explore 31 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICSChapter:CENGAGE PHYSICS DPPExercise:Multiple Correct Answer Type
Explore 54 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICSChapter:CAPACITOR AND CAPACITANCEExercise:Integer
Explore 5 Videos
- CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONBook:CENGAGE PHYSICSChapter:CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONExercise:Question Bank
Explore 38 Videos
Similar Questions
Two lines cut on the axis of x intercepts 4and−4 and on the axis of y intercepts 2 and 6 respectively. Find the coordinates of their point of intersection.
View SolutionTaking horizontal ground as xz- plane and y-axis vertically upwards. A particle is projected from the horizontal ground from a point whose position vector is ˆiˆk meter with initial velocity from the origin when it hits ground is given by 15[11ˆi+nˆk], find n. (Take g=10m/s2 in negative y - direction)
View Solution
Knowledge Check

A particle is projected from the horizontal x-z plane, in vertical x-y plane where x-axis is horizontal and positive y-axis vertically upwards. The graph of y coordinate of the particle v/s time is as shown . The range of the particle is √3. Then the speed of the projected particle is:A√3msB√4034msC2√5msD√28msA particle is projected upwards with a velocity of 110m/sec at an angle of 60∘ with the vertical. Find the time when the particle will move perpendicular to its initial direction, taking g =10m/sec2
A10 secondsB22 secondsC5 secomdsD10√3 secondsA ball is projected towards right from point A at an angle θ with vertical. A system imparts an acceleration gtanθ to the ball towards left along negative x-axis. The ball will return to ground at :
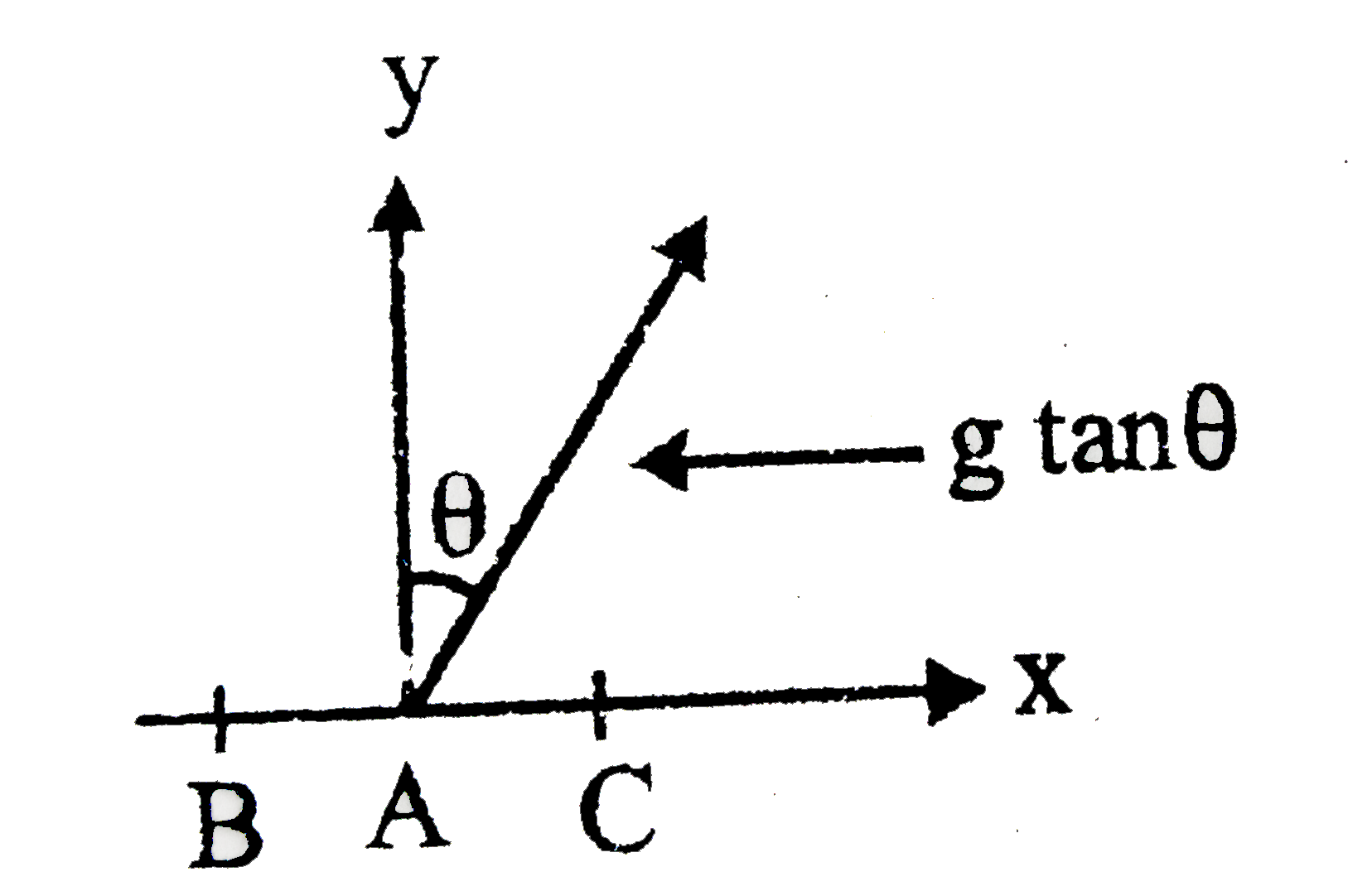 Aat point A.Bleft to poin ACright to point ADinformation is not suffcient
Aat point A.Bleft to poin ACright to point ADinformation is not suffcient
A particle of mass m is released in vertical plane from a point P at x=x0 on the x-axis. It falls vertically parallel to the y-axis. Find the torque τ acting on the particle at a time about origin.

View SolutionA particle is projected upwards with a velocity of 100m/sec at an angle of 60∘ with the vertical. Find the time when the particle will move perpendicular to its initial direction, taking g=10m/sec2.
View SolutionTwo particles are moving along x-axis. Particle-1 starts from x=−10m with velocity 4m/s along negative x-direction and acceleration 2m/s2 along positive x-direction. Particle-2 starts from x=+2m with velocity 6m/s along positive x-direction and acceleration 2m/s2 along negative x-direction.
(a) Find the time when they collide.
(b) Find the x-coordinates where they collide. Both start simultaneously.
View SolutionA particle is projected from the ground . Point of projection is taken as origin, horizontal direction as X-axis and verticle upward direction ass Y-axis. Equation of trajectory of the partcle is y=αx−βx2. Horizontal range of the projectile is
View SolutionThe coordinates of a point A on y-axis, at a distance of 4 units from x-axis and below it, are
View Solution

