An object is projected with a velocity of 20ms making an angle of 45∘ with horizontal. The equation for the trajectory is h=Ax−Bx2 where h is height, x is horizontal distance, A and B are constants. The ratio A:B is (g=ms−2)
1:5
5:1
1:40
40:1
The correct Answer is:D
To solve the problem, we need to derive the constants A and B from the trajectory equation of the projectile motion. The trajectory is given as h=Ax−Bx2, where h is the height, x is the horizontal distance, and A and B are constants.
1. Identify the Initial Conditions:
The object is projected with a velocity u=20m/s at an angle θ=45∘.
2. Resolve the Initial Velocity:
The horizontal and vertical components of the initial velocity can be calculated as:
ux=ucosθ=20cos45∘=20×1√2=10√2m/s
uy=usinθ=20sin45∘=20×1√2=10√2m/s
3. Determine Time of Flight:
The time of flight t can be calculated using the formula:
t=2uyg=2×10√210=2√2s
4. Calculate Horizontal Distance:
The horizontal distance x covered in time t is:
x=ux⋅t=(10√2)⋅(2√2)=40m
5. Find the Height at Horizontal Distance:
The height h at any time t can be expressed as:
h=uyt−12gt2
Substituting t=xux:
h=10√2⋅x10√2−12g(x10√2)2
Simplifying this gives:
h=x−g2(10√2)2x2
h=x−g400x2
6. Identify Constants A and B:
From the trajectory equation h=Ax−Bx2, we can identify:
- A=1
- B=g400
7. Calculate the Ratio A:B:
Now, we need to find the ratio A:B:
Ratio=AB=1g400=400g
8. Substituting the Value of g:
Given g=10m/s2:
Ratio=40010=40
Final Answer:
The ratio A:B is 40:1.
The object is projected with a velocity u=20m/s at an angle θ=45∘.
The horizontal and vertical components of the initial velocity can be calculated as:
ux=ucosθ=20cos45∘=20×1√2=10√2m/s
uy=usinθ=20sin45∘=20×1√2=10√2m/s
The time of flight t can be calculated using the formula:
t=2uyg=2×10√210=2√2s
The horizontal distance x covered in time t is:
x=ux⋅t=(10√2)⋅(2√2)=40m
The height h at any time t can be expressed as:
h=uyt−12gt2
Substituting t=xux:
h=10√2⋅x10√2−12g(x10√2)2
Simplifying this gives:
h=x−g2(10√2)2x2
h=x−g400x2
From the trajectory equation h=Ax−Bx2, we can identify:
- A=1
- B=g400
Now, we need to find the ratio A:B:
Ratio=AB=1g400=400g
Given g=10m/s2:
Ratio=40010=40
The ratio A:B is 40:1.
Similar Questions
An object is projected with a velocitiy of 20m/s making an angle of 45∘ with horizontal. The equation for trajectory is h=Ax−Bx2 where h is height x is horizontal distance. A and B are constants. The ratio A.B is x0.1. Find value of x.(g=10m/s2)
View SolutionA particle is projected with a velocity of 10√2m/s at an angle of 45∘ with the horizontal. Find the interval between the moments when speed is √125m/s(g=10m/s2)
View Solution
Knowledge Check
- Question 1 - Select One
A body is projected from ground with speed 20 m/s making an angle of 45∘ with horizontal. The equation of path is h=Ax−Bx2, where h is height, x is horizontal distance, A and B are constant. The ratio A : B is :-
(g=10m/s2)A1 : 5B5 : 1C1 : 40D40 : 1 - Question 2 - Select One
An object is projected with a velocity of 10m/s at an angle 45∘ with horizontal. The equation of trajectory followed by the projectile is y=ax−βx2, the ratio α/β is
A5B10C15D20 - Question 3 - Select One
A particle is projected with velocity of 10ms at an angle of 15° with horizontal.The horizontal range will be(g=10ms2)
A10mB5mC2.5mD1m
A particle is projected with velocity 20√2m/s at 45∘ with horizontal. After 1s(g=10m/s2) match the following table
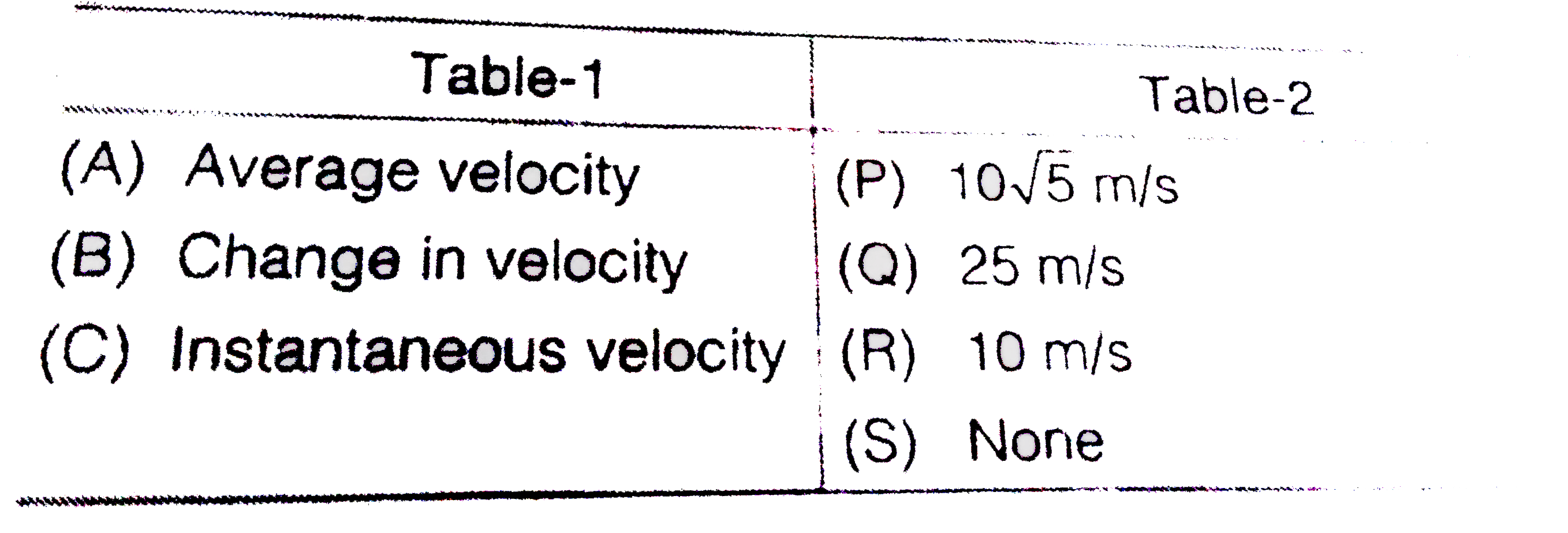 View Solution
View SolutionA particle is projected with velocity 50 m/s at an angle 60∘ with the horizontal from the ground. The time after which its velocity will make an angle 45∘ with the horizontal is
View SolutionA stone is projected with a velocity 20√2m/s at an angle of 45∘ to the horizontal.The average velocity of stone during its motion from starting point to its maximum height is
View SolutionA projectile is thrown with a velocity of 20 m/s, at an angle of 60∘ with the horizontal. After how much time the velocity vector will make an angle of 45∘ with the horizontal (in upward direction) is (take g=10m/s2)−
View SolutionA particle is projected with an initial velocity of 200m/s in a direction making an angle of 30∘ with the vertical. The horizontal distance covered by the particle in 3s is
View Solution

