A particle is projected with velocity 50 m/s at an angle 60∘ with the horizontal from the ground. The time after which its velocity will make an angle 45∘ with the horizontal is
2.5 s
1.83 s
2.37 s
3.72 m
The correct Answer is:B
To solve the problem step by step, we need to analyze the motion of the particle projected at a velocity of 50 m/s at an angle of 60 degrees with the horizontal. We want to find the time at which the velocity of the particle makes an angle of 45 degrees with the horizontal.
Step 1: Break down the initial velocity into components
The initial velocity u=50m/s can be resolved into horizontal and vertical components using trigonometric functions.
- Horizontal component ux=ucos(60∘)=50⋅12=25m/s
- Vertical component uy=usin(60∘)=50⋅√32=25√3m/s
Step 2: Determine the conditions for the velocity to make a 45-degree angle
For the velocity to make an angle of 45 degrees with the horizontal, the vertical component of the velocity vy must equal the horizontal component vx.
Step 3: Express the horizontal and vertical components of velocity at time t
Since there is no acceleration in the horizontal direction, the horizontal component remains constant:
- vx=ux=25m/s
The vertical component of velocity changes due to gravity:
- vy=uy−gt
- vy=25√3−10t
Step 4: Set up the equation for the condition vy=vx
We set the vertical component equal to the horizontal component:
25√3−10t=25
Step 5: Solve for t
Rearranging the equation gives:
25√3−25=10t
10t=25(√3−1)
t=25(√3−1)10
t=2.5(√3−1)
Calculating √3≈1.732:
t=2.5(1.732−1)
t=2.5(0.732)
t≈1.83s
Step 6: Check for the second instance when the angle is 45 degrees
The particle will also make a 45-degree angle on its way down. The vertical component will be negative:
−vy=uy−gt
Setting this equal to vx:
−(25√3−10t)=25
This leads to:
10t=25√3+25
t=25(√3+1)10
t=2.5(√3+1)
Calculating this gives:
t≈2.5(1.732+1)
t≈2.5(2.732)
t≈6.83s
Final Answer
The times at which the velocity of the particle makes a 45-degree angle with the horizontal are approximately 1.83s and 6.83s.
The initial velocity u=50m/s can be resolved into horizontal and vertical components using trigonometric functions.
- Vertical component uy=usin(60∘)=50⋅√32=25√3m/s
For the velocity to make an angle of 45 degrees with the horizontal, the vertical component of the velocity vy must equal the horizontal component vx.
Since there is no acceleration in the horizontal direction, the horizontal component remains constant:
- vx=ux=25m/s
- vy=uy−gt
- vy=25√3−10t
We set the vertical component equal to the horizontal component:
25√3−10t=25
Rearranging the equation gives:
25√3−25=10t
10t=25(√3−1)
t=25(√3−1)10
t=2.5(√3−1)
t=2.5(1.732−1)
t=2.5(0.732)
t≈1.83s
The particle will also make a 45-degree angle on its way down. The vertical component will be negative:
−vy=uy−gt
Setting this equal to vx:
−(25√3−10t)=25
This leads to:
10t=25√3+25
t=25(√3+1)10
t=2.5(√3+1)
Calculating this gives:
t≈2.5(1.732+1)
t≈2.5(2.732)
t≈6.83s
The times at which the velocity of the particle makes a 45-degree angle with the horizontal are approximately 1.83s and 6.83s.
Topper's Solved these Questions
- MOTION IN A PLANEBook:AAKASH INSTITUTEChapter:MOTION IN A PLANEExercise:Assignement section -C Objective (More than one option is correct)
Explore 5 Videos
- MOTION IN A PLANEBook:AAKASH INSTITUTEChapter:MOTION IN A PLANEExercise:Assignement section -D (Linked Comprehension)
Explore 8 Videos
- MOTION IN A PLANEBook:AAKASH INSTITUTEChapter:MOTION IN A PLANEExercise:Assignement section -A Objective (one option is correct)
Explore 50 Videos
- MOCK_TEST_17Book:AAKASH INSTITUTEChapter:MOCK_TEST_17Exercise:Example
Explore 15 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - D)
Explore 15 Videos
Similar Questions
Knowledge Check
A projectile is thrown with a velocity of 20 m/s, at an angle of 60∘ with the horizontal. After how much time the velocity vector will make an angle of 45∘ with the horizontal (in upward direction) is (take g=10m/s2)−
A√3secB1/√3secC(√3−1secDNone of theseA ball is projected with a velocity 20√3ms−1 at angle 60∘ to the horizontal. The time interval after which the velocity vector will make an angle 30∘ to the horizontal is (Take, g=10ms−2)
A5sB2sC1sD3sA particle is projected with speed 10m/s at angle 60∘ with the horizontal. Then the time after which its speed becomes half of initial.
A12 secB1 secC√3/2secD√3/2sec
If a particle is projected with a velocity 49m/sec. making an angle 60∘ with the horizontal, its time of flight is given by
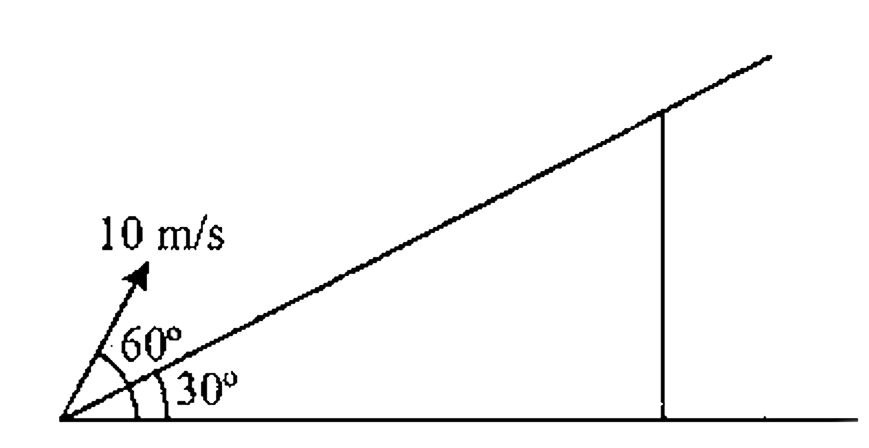
View SolutionA particle is thrown at time t=0 with a velocity of 10 m/s at an angle of 60∘ with the horizontal from a point on an incline plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is :
View Solutiona particle is projected down on inclined plane with a velocity of 21m/s at an angle of 60∘ with the horizontal its range on the inclined plane inclined at an angle of 30∘ with the horizontal is
View Solutiona particle is projected down on inclined plane with a velocity of 21m/s at an angle of 60∘ with the horizontal its range on the inclined plane inclined at an angle of 30∘ with the horizontal is
View SolutionTwo particle are projected with same initial velocities at an angle 30∘ and 60∘ with the horizontal .Then
View Solution

