Time for 20 oscillations of a pendulum is measured as t1=39.6s,t2=39.9 and t3=39.5s. What is the precision in the measurements ? What is the accuracy of the measurement ?
To solve the problem, we need to determine the precision and accuracy of the measurements of the time taken for 20 oscillations of a pendulum. The measurements provided are t1=39.6s, t2=39.9s, and t3=39.5s.
Step 1: Determine the Precision of the Measurements
Precision is defined as the smallest division of the measuring instrument, also known as the least count. In this case, since the measurements are given to one decimal place, the least count is:
Precision=0.1s
Step 2: Calculate the Mean Value of the Measurements
To find the accuracy, we first need to calculate the mean (average) of the three measurements. The mean value T is given by:
T=t1+t2+t33=39.6+39.9+39.53
Calculating this:
T=119.03=39.7s
Step 3: Calculate the Absolute Errors
Next, we calculate the absolute errors for each measurement. The absolute error for each measurement is defined as the difference between the mean value and the individual measurements:
- For t1:
Δt1=T−t1=39.7−39.6=0.1s
- For t2:
Δt2=T−t2=39.7−39.9=−0.2s
- For t3:
Δt3=T−t3=39.7−39.5=0.2s
Step 4: Calculate the Mean Absolute Error
The mean absolute error (MAE) is calculated using the absolute values of the errors:
Mean Absolute Error=|Δt1|+|Δt2|+|Δt3|3
Calculating this:
Mean Absolute Error=0.1+0.2+0.23=0.53≈0.1667s
Step 5: Determine the Accuracy of the Measurement
The accuracy of the measurement is typically expressed as the mean absolute error. Thus, we can state the accuracy as:
Accuracy=±0.2s(rounded to one decimal place)
Final Results
- Precision: 0.1s
- Accuracy: ±0.2s
Precision is defined as the smallest division of the measuring instrument, also known as the least count. In this case, since the measurements are given to one decimal place, the least count is:
To find the accuracy, we first need to calculate the mean (average) of the three measurements. The mean value T is given by:
Next, we calculate the absolute errors for each measurement. The absolute error for each measurement is defined as the difference between the mean value and the individual measurements:
Δt1=T−t1=39.7−39.6=0.1s
Δt2=T−t2=39.7−39.9=−0.2s
Δt3=T−t3=39.7−39.5=0.2s
The mean absolute error (MAE) is calculated using the absolute values of the errors:
The accuracy of the measurement is typically expressed as the mean absolute error. Thus, we can state the accuracy as:
- Precision: 0.1s
- Accuracy: ±0.2s
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICSChapter:CENGAGE PHYSICS DPPExercise:single correct type
Explore 14 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICSChapter:CAPACITOR AND CAPACITANCEExercise:Integer
Explore 5 Videos
- CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONBook:CENGAGE PHYSICSChapter:CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONExercise:Question Bank
Explore 38 Videos
Similar Questions
Time for 20 oscillations of a pendulum is measured as t1=39.6s,t2=39.9s,t3=39.5. What is the precision in the measurements ? What is the accuracy of the measurement ?
View SolutionThe least count of a stop watch is 0.2 second. The time of 20 oscillations of a pendulum is measured to be 25 seconds. The maximum percentage error in this measurement is found to be 0.x%. What is the value of x?
View Solution
Knowledge Check
A student measures time for 20 oscillations of a simple pendulum as 30s, 32s, 35s and 31s. If the minimum division in the measuring clock is 1s, then correct meant time in second is
A32±3B32±1C32±2D32±5If the time period of oscillation of a pendulum is measured as 2.5 second using a stop watch with the least count 12 second, then the permissible error in the measurement is
A10%B30%C15%D20%The least count of a stop watch is (1/5)s. The time 20 oscillations of a pendulum is measured to be 25s. The maximum percentage error in this measurement is
A8%B1%C0.8%D16%
The period of oscillation of a simple pendulum is T=2π√L/g. Measured value of L is 20.0cm known to 1mm accuracy and time for 100 oscillations of the pendulum is found to be 90 s using a wrist watch of 1 s resolution. What is the accuracy in the determination of g?
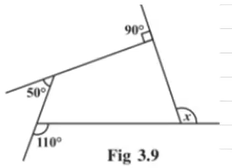
View SolutionFind measure x in Fig 3.9.
View SolutionThe time period of a simple pendulum is given by T=2π√L/g, where L is length and g acceleration due to gravity. Measured value of length is 10cm known to 1mm accuracy and time for 50 oscillations of the pendulum is 80 s using a wrist watch of 1 s resloution. What is the accuracy in the determination of g?
View SolutionThe time period of a simple pendulum is given by T=2π√lg . The measured value of the length of pendulum is 10 cm known to a 1 mm accuracy. The time for 200 oscillations of the pendulum is found to be 100 second using a clock of 1 s resolution. The percentage accuracy in the determination of 'g' using this pendulum is 'x'. The value of 'x' to the nearest integer is,
View SolutionThe least count of a stop watch is 0.2 s, The time of 20 oscillations of a pendulum is measured to be 25s. The percentage error in the time period is
View Solution

