The line x+y=1 meets X-axis at A and Y-axis at B,P is the mid-point of AB,P1 is the foot of perpendicular from P to OA,M1 is that of P1 from OP,P2 is that of M1 from OA,M2 is that of P2 from OP,P3 is that of M2 from OA and so on. If Pn denotes theb nth foot of the perpendicular on OA, then find OPn
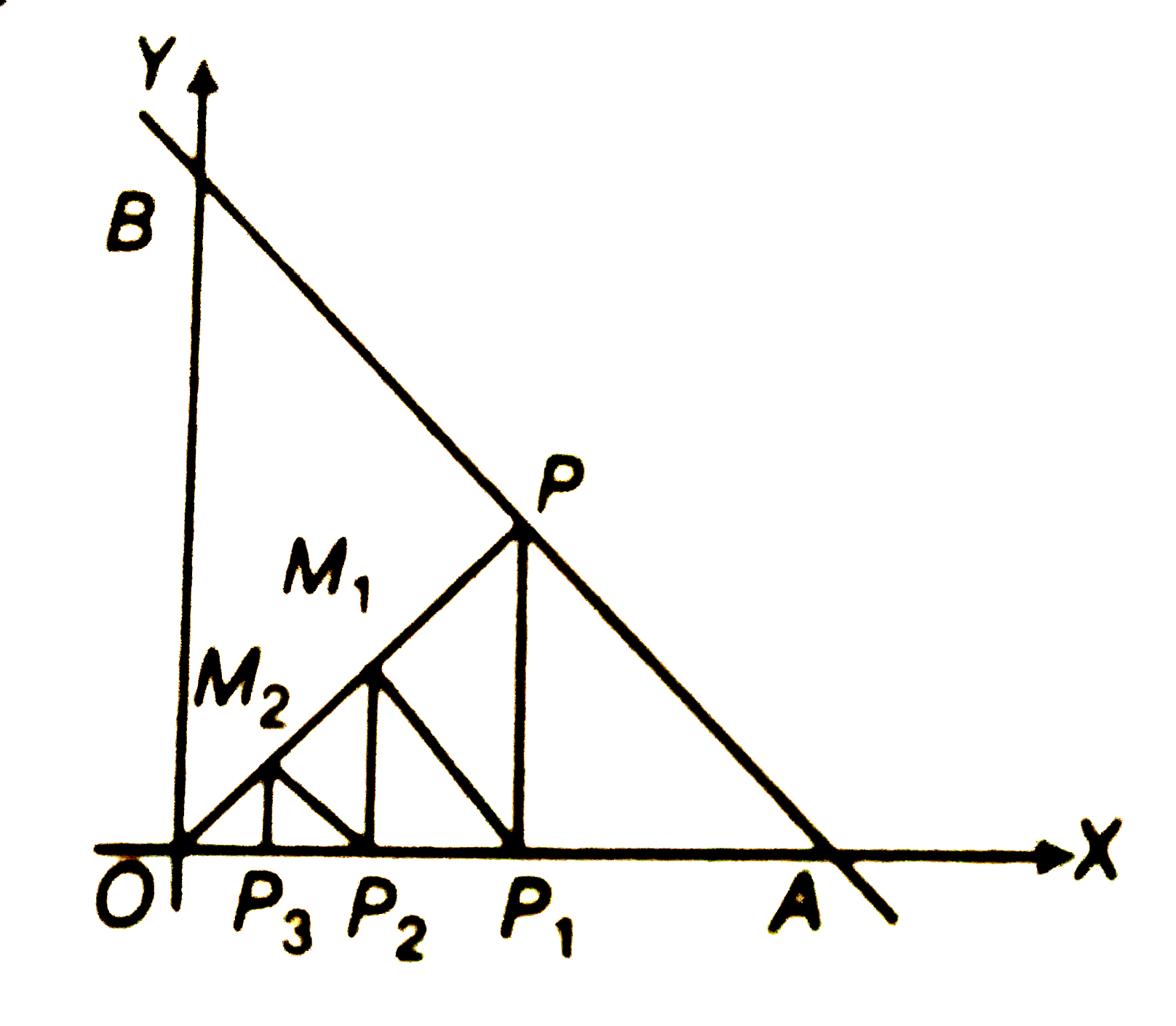 .
.
We have, (OMn−1)2=(OPn)2+(PnMn−1)2
(OMn−1)2=(OPn)2+(OPn)2=2(OPn)2=2α2n[ say
Also, (OPn−1)2=(OMn−1)2+(Pn−1Mn−1)2
⇒α2n−1=α2n+12α2n−1⇒α2n=14α2n−1
⇒αn=12αn−1
⇒OPn=αn=122αn−2=...=12n
∴OPn=(12)n
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise For Session 15videos
SEQUENCES AND SERIES
- BOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise For Session 211videos
SEQUENCES AND SERIES
- BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)21videos
PROPERTIES AND SOLUTION OF TRIANGLES
- BOOK - ARIHANT MATHSCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)12videos
SETS, RELATIONS AND FUNCTIONS
Similar Questions
The line x+y=1 meets X-axis at A and Y-axis at B,P is the mid-point of AB,P1 is the foot ofperpendicular from P to OA,M1, is that of P1, from OP;P2, is that of M1 from OA,M2, is that of P2, from OP;P3 is that of M2, from OA and so on. If Pn denotes the nth foot of the perpendicular on OA, then find OPn.
View SolutionThe foot of the perpendicular from the point P(1,3,4) to the plane 2x-y+z+3=0 is
View Solution
Knowledge Check
- Question 1 - Select One
Consider the plane π1:2x−3y+4z+9=0 and the point P(1,-2,3).

A is the foot of perpendicular from P to π1. Equation of PA is _________ .Ax−12=y+2−3=z−34Bx+12=y−2−3=z+34C→r=(ˆi+2ˆj−3ˆk)+λ(2ˆi−3ˆj+4ˆk)D→r=(ˆi−2ˆj+3ˆk)+λ(ˆi−2ˆj+3ˆk) - Question 2 - Select One
The length of the perpendicular from P(1,6,3) to the line x1=y−12=z−23is
A3B√11C√13D5 - Question 3 - Select One
If the distance of the point P(1,−2,1) from the plane x+2y−2z=α,whereα>0,is5, then the foot of the perpendicular from P to the place is a. (83,43,−73) b. (43,−43,13) c. (13,23,103) d. (23,−13,−53)
A(83,43,−73)B(43,−43,13)C(13,23,103)D(23,−13,52)
Find the coordinate of the foot of the perpendicular from P(2,1,3) on the line joinint the points A(1,2,4)andB(3,4,5)
View SolutionFind the coordinates of the foot of the perpendicular from P(2,1,3) on the lines joining the points A(1,2,4)andB(3,4,5).
View SolutionFind the coordinates of the foot of the perpendicular drawn from the point P(1,-2) on the line y = 2x +1. Also, find the image of P in the line.
View SolutionS is the point (4,0) and M is the foot of the perpendicular drawn from a point P to the y-axis. If P moves such that the distance PS and PM remain equal find the locus of P.
View SolutionLet L:x−2y+4z=9 be a plane, P(2,1,−1) be a point and O, be the Origin. Q is the foot of the perpendicular from P on the plane L, then (OP)2+(PQ)2 is equal to
View Solution

